9.5 Генератор пвп на основі багатомодульних перетворень

Нижче пропонується метод генерування псевдо випадкових послідовностей основі багатомодульного перетворення в скінченному полі Галуа , що дозволяє генерувати ПВП з довільним алфавітомm, заданим періодом повторення та певними властивостями

Ще раз відмітимо, що нині проблемною, що вимагає свого вирішення, є задача розробки методів і засобів генерування псевдовипадкових послідовностей (ПВП) із необхідними властивостями необоротності, нерозрізнюваності, непередбачуваності, заданним наперед періодом та довільною (певною) основою алфавіту m. Вона може бути вирішена на основі використання перетворень, що отримали назву багатомодульних[ 316, 317]. Деякі положення багатомодульного перетворення для простого поля опубліковані в [316]. В цій роботі запропоновано метод генерування ПВП на основі багатомодульного перетворення в полі Галуа . Він дозволяє генерувати ПВП з довільним алфавітом m, заданим періодом повторення та певними, але недостатньо дослідженими властивостями нерозрізнюваності.

Але в указаній роботі залишились нерозглянутими питання управлінння ключами генератора, а по суті розробки криптографічного генератора, а також оцінки рівнів гарантій такого генератора ПВП в частині необоротності, непередбачуваності та нерозрізнюваності [ 291, 315]. Дослідження роботи носять також обмежений характер, так як вони проведені тільки для багатомодульних перетворень над простим полем Галуа

Ми розглянемо задачу розробки методу генерування ПВП з певним алфавітом символів m, на основі багатомодульних перетворень з використання елементів довільного поля Галуа . Зрозуміло, що відносно цього методу необхідно провести комплекс теоретичних та експериментальних досліджень в частині визначення необхідних та достатніх умов забезпечення заданого періоду повторення, основи алфавіту, ймовірності появи символів алфавіту на періоді повторення, якості необоротності, непередбачуваності та нерозрізнюваності с точки зору гарантій [291,317].

9.4.1 Метод багато модульного перетворення в скінченному полі .

Розглянемо метод генерування ПВП з певним алфавітом символів, скажемо m, на основі багатомодульних перетворень, але на основі використання елементів уже довільного скінченного поля Галуа . Для загального випадку будемо вважати, що здійснюється k перетворень елементів розширення поля Галуа, відповідно за модулямита останнім модулем m. Загальними параметрами, яких достатньо для того, щоби генерувати елементиполя, є кортеж, де– незвідний поліном степеню n над полем, а– первісний елемент, вибраний із множинипорядку, де– функція Ейлера [ 196 ]. В цьому випадку генерування (формування) елементів поля здійснюється за правилом

. (9.101 1 )

Показано [259], що при виконанні вказаних вище вимог до кортежу , (9.101 ) породжує скінченне поле Галуа з періодом повторення. Замітимо, що вказане справедливо дляі наступних простих чисел. Причому, при p=2 будемо мати розширення над полем Галуа.

Далі, нехай будуть кортежами загальних параметрів, наприклад поліномів (в тому числі незвідних),, а– їх степені. В подальшому незвідність поліномів нам потрібна для того, щоби при необхідності забезпечити їх взаємну простоту [ 259 ].

Також нехай степені поліномів (в тому числі незвідних) задовольняють вимогам

, , … ,, (9.102 2 )

причому основа алфавіту m є довільним числом, а також виконуються нерівності

, ,…,,. (9.103 3 )

Справедливим є твердження 9.1.

Твердження 9. 1. Детермінований генератор ПВП, що функціонує згідно багато модульного перетворення

(9.104 )

,

де кортежі загальних параметрів, m – певне натуральне число, k – ступень багато модульності,(не обов’язково просте), m ціле натуральне, забезпечує генерування ПВП (символів) з періодом повторення, рівно ймовірно і з певною основою алфавіту m, за умови, що:

виконуються умови (9.101 ) – ( 9.103 ) ;

модулі (пари поліномів)

(9.104 )

є взаємо простими, а кортеж () є довільним.

В (9.104 ) запис – означає, що модуль m подається у вигляді полінома.

При виконанні умов (9.104)–(9.105) забезпечується генерування ПВП (символів) з такими властивостями та характеристиками:

певною основою алфавіту m;

періодом повторення ;

символи генеруються рівноймовірно або "практично" рівно ймовірно;

ансамблем ізоморфізмів .

Справедливим також є твердження 9.2.

Твердження 9.2. Детермінований генератор ПВП, що функціонує згідно алгоритму багатомодульного перетворення

(9.106 )

,

де K0+i є плинний ключ генератора, причому K0 є початковим ключем, а i – ключем сеансу, є не оборотним зі складністю не нижче чим О(n)[320].

Розглянемо далі частковий випадок твердження 9.1 та 9.2 для 3-ьох модульного перетворення. В даному випадку елементи розширення поля Галуа також генеруються згідно (9.101 ). Але (9.102 ) – (9.106 ) приймають вид (9.107 ) – (9.110 ).

. (9.107 )

. (9.108 )

. (9.109 )

, (9.110 )

де в (9.110) K0+i є плинний ключ генератора, K0 початковий, а i – ключ сеансу.

Для умов (9.107) – (9.110) твердження 9.1 для трьох модульного перетворення подамо у вигляді теореми 9.1 .

Теорема 1. Детермінований генератор ПВП, що функціонує згідно трьох модульного перетворення на основі (1 ), за правилами

(9.111 )

або

(9.112 )

при виконанні умов (9.102) – (9.108), забезпечує генерування ПВП (символів) чисел з певною основою алфавіту m, періодом повторення , рівно ймовірною появою символів на періоді повтореннята ансамблем ізоморфізмів.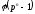

Таким чином , теорема 1 для 3-ьох модульного перетворення доведена. Також необхідно замітити що наведене доведення теореми 1 може бути розповсюджене і на випадок k модульного перетворення, зрозуміло за умови коли пари поліномів є взаємо простими, а кортежє довільним, мається на увазі значення модуля m.

У цілому процедура генерування ПВП на основі багатомодульного перетворення може бути зведеною до наступного.

1. Ввести або генерувати загальносистемні параметри – кортежі загальних параметрів згідно вимог твердження 1.

2. Ввести або інсталювати таємний ключ генератора ,.

3. Обчислити початкове значення генератора , використовуючи правило

, (9.120)

де – основний модуль перетворення.

4. Обчислити елемент 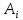генератора, використовуючи правило

, (9.121)

де 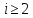– номер елемента ПВП, що генерується,–-й елемент послідовності над полем поширення.

5. Обчислити елемент ДГВЧ, використовуючи правило

, (9.122)

де .

6. Обчислити елемент ДГВЧ, використовуючи правило

, (9.123 )

де – номер елемента ПВП, що генерується,– проміжні модулі.

7. Якщо потрібно, то обчислити -е геш-значення відта прийняти його в якості-го випадкового слова, тобто

. (9.124 )

Схема алгоритму (варіант), що реалізує наведений вище метод генерування ДГВЧ, наведена на рис. 9.13.

Рис. 9.13 – Схема алгоритму генерування детермінованих випадкових

послідовностей в скінченному полі порядку - 1 методом багатомодульного перетворення

Висновки

На нинішній час розроблено ряд методів та на їх основі засобів формування ПВП, Їх особливістю є те, що вони будуються, як правило, для двійкової основи . Важливою і необхідною є задача розробки методів і засобів генерування ПВП із необхідними властивостями випадковості та довільною (певною) основою алфавіту. В якості перспективного, на наш погляд, класу таких перетворень необхідно назвати клас багатомодульних перетворень.

Детермінований генератор ПВП, що функціонує згідно трьох модульного перетворення на основі (9.111 ) або (9.112 ) при виконанні умов (9.102 ) – (9.108 ), забезпечує генерування ПВП (символів) чисел з певною основою алфавіту m, періодом повторення , рівно ймовірною появою символів на періоді повтореннята ансамблем ізоморфізмів.

9.4.2 Властивості ПВП багатомодульних перетворень.

Як і вище розглядається метод генерування ПВП з певним алфавітом символів, скажемо m, на основі багатомодульних перетворень в скінченному полі Галуа , . n ≥ 1. Вважається , що здійснюється k перетворень елементів розширення поля Галуа, відповідно за модулями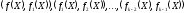та останнім модулем m. Загальними параметрами є кортеж, де– незвідний поліном степеню n над полем, а– первісний елемент, вибраний із множинипорядку, де– функція Ейлера [ 196 ].

Будемо розглядати також частковий випадок теореми 1 для 3-ьох модульного перетворення. В даному випадку елементи розширення поля Галуа також генеруються згідно (9.101 ). Пр цьому (9.102 ) – (9.106 ) приймають наступний вигляд:

і ;

,

де як і вище K0+i є плинний ключ генератора, K0 початковий, а i – ключ сеансу.

Оцінка складності обернення генератора ПВП

.

Проведемо оцінку складності дискретного логарифмування для трьох та багато модульного перетворень.

У випадку для скінченного поля Галуа маємо

, (9.125)

де Х = К0 +i належить визначенню, за умови що відомою є деяка послідовність символів bi, первісний елемент та кортеж параметрів (Р, Р1, m).

При здійснення атаки « груба сила » можуть бути застосованими такі основні методи – перебирання ключів, таблична атака та атака зі словником [ ].

При застосуванні атаки « груба сила » вважається, що довжина ключа k не більш ніж довжина генерованої ПВП і порушник перебираючи ключ X, робить спробу отримати значення

. (9.126 4.54)

При виконанні умови (9.126) буде визначено ключ генератора.

Для оцінки можливостей реалізації атаки «груба сила» можуть бути використаними такі показники як Nk – число ключів, безпечний час tб , Pp – ймовірність успішного крипто аналізу тощо [4, 5, 13 ]. Значення можна обчислити [13]:

, (9.127 12 4.55)

де потужність крипто аналітичної системи,=3,15 10⁷ число секунд у році.

Таблична атака та атака зі словником ґрунтуються на використанні математичного апарату «парадоксу про день народження» – методом створення колізій [5 ]. Для даного методу параметри ймовірність колізій , число спроб крипто аналітика k та повна множина можливих вихідних значень n пов’язані між собою таким параметричним рівнянням [106]

(9.128 4.56)

або в кінцевому вигляді

. (9.129 4.57)

Співвідношення (9.129) дозволяє оцінити число експериментів, які необхідно виконати для здійснення колізії з застосуванням математичного апарату «парадоксу про день народження».

В ряду випадків пару « ключ генератора – вихідний блок ПВП » можна отримати методом словника. В цьому випадку генеруються або збираються пари «ключ генератора – вихідний блок ПВП » в спеціальному словнику. А пошук ключа здійснюється засобом знаходження реалізації ПВП, що співпадає з виходом генератора по словнику.

Проведемо аналіз можливостей та умов реалізації атаки типу « груба сила», яка проводиться відносно (9.125) з метою визначення елемента поля . У випадку (9.125) для досягнення (9.126) розглянемо модель відображення m – ічного символу в р – ічний. Нехай довжини символів в двійковому поданні будутьтавідповідно для модулів p, p1 та m. Визначимо ймовірність угадування по bi символу р – ічного символу, а по суті визначення.

Теорема 9.1. Для умов (9.125) ймовірність правильного відображення (вгадування) Рпв m-ічного символу в р-ічнийвизначається співвідношенням

, (9.130 4.58)

де lp та lm двійкове подання довжин символів p та m.

Розглянемо доведення теореми. При довжині m-ічного символу в двійковому поданнічисло можливих його станів визначається як. При перетворенні за модулемдовжина символу в двійковому поданні буде, а число можливих станів визначається як. При цьому степінь розширення алфавіту можна оцінити як

. (9.131 4.59)

При перетворенні за модулем p довжина символу в двійковому поданні буде , а число можливих станів визначається як. Степінь розширення алфавіту при переході до перетворення за модулем p буде

. (9.132 4.59)

Відповідно ймовірність вгадування символу алфавіту за модулем визначається як

. (9.133 4.60)

Ймовірності вгадування символу алфавіту за модулем р визначається як

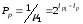. (9.134 4.61)

Таким чином теорема доведена.

Загальна ймовірность вгадування символу алфавіту Рв за модулем р при переході від m-ічного джерела до p-ічного буде визначатись перемноженням подій та, тобто

. (9.135 4.62)

Використовуючи (9.135), можна також визначити складність вгадування одного символу алфавіту за модулем р при переході від m-ічного джерела до p-ічного, як

. (9.136 4.62)

Таким чином, при застосуванні схеми генератора без гешування складність відновлення ключавизначається

. (9.137 .63)

Для випадку застосування схеми генератора з вгадуванням елемента поля, розв’язком дискретного логарифму та гешуванням складність відновлення ключавизначається

. (9.138 4.64)

Необхідно відмітити, що вирази (9.137) та (9.138) отримані для випадку, коли ПВП виробляється засобом використання тільки одного m-ічного символу. Якщо для вироблення ПВП використовується µ m-ічних символи, а значення i збільшується по відомому правилу, то (9.137) та (9.138) можна використовувати для оцінки криптографічної стійкості генератора ПВП, що пропонується. Якщо i збільшується по не відомому правилу, то необхідно вирішувати додатково ще і задачу визначення правила його зміни. Але, так як правило зміни i будемо вважати відомим крипто аналітику, то (9.137) та (9.138) рекомендується для оцінки складності обернення генераторів ПВП розглядаєж\ємого типу.

В табл.. 9.17 наведені оцінки складності обернення генератора ПВП згідно (9.137) та (9.138). Аналіз даних таблиці 9.17 дозволяє зробити висновок про те, що складність обернення генератора носить експоненційний характер і є більшою за складність методу «груба сила».

Таблиця.9.17- Складність обернення генераторів.

p, p1, m Метод		2256, 2128, 28	2256, 2128, 264	2512, 2256, 28	21024, 2512, 2256	22048, 21024, 2512
Iвд		9.0543∙10089	7.0143∙10072	2.1618∙10172	1.4827∙10259	1.1867∙10500
Iвдг	n	6.1103∙10113	8.4798∙10096	2.6135∙10196	1.7925∙10283	1.4346∙10524
	160
	256	1.7199∙10128	2.3868∙10111	7.3562∙10210	9.0453∙10297	4.0381∙10538
	384	3.1726∙10147	4.4029∙10130	1.3570∙10230	9.3071∙10316	7.4490∙10557
	512	9.8524∙10166	8.1219∙10149	2.5031∙10249	1.7168∙10336	1.3741∙10577

Розглянемо ще один підхід до вирішення задачі обернення генераторів ПВП виду (9.125), що ґрунтується на класах лишків. Для цього подамо (9.125) у такому вигляді

, .

, .

(9.139 4.65)

Безпосередній аналіз (9.139) показує, що є невідомими та належать визначенню. Тепер врахуємо що правило зміниє відомим. На основі (9.139) можна скласти систему рівнянь виду

(9.140 4.66)

Аналіз системи рівнянь (9.139) показує, що кожне нове рівняння в системі добавляє 2 невідомих, але при цьому існує лінійна залежність між татощо. В цілому в системі k-го порядку буде 2k+1 невідомих, якщо навіть вважати що тількиє невідомим.

Таким чином, система рівнянь виду (9.140) з 2k+1 невідомими розв’язку не має. Також необхідно відмітити, що по аналогії з трьох модульним перетворенням, при багатомодульному перетворенні кожне додаткове модульне перетворення добавляє 2 невідомих.

Таким чином, властивості необоротності генератора ПВП по суті пов’язані з розв’язком дискретних логарифмічних рівнянь, наприклад для трьох модульним перетворенням виду (9.106) відносно i та K0+i.

Для успішного крипто аналізу генератора необхідно спочатку вирішити дискретне логарифмічне рівняння та знайти елемент – прообраз. В цьому випадку спочатку необхідно знайти прообраз відповідного елемента поля , а потім вирішити дискретне логарифмічне рівняння зі складністю ().

Для умови (9.125) ймовірність правильного відображення (вгадування) m-ічногосимволу в р-ічнийвизначається співвідношенням (9.130).

Аналіз системи рівнянь (9.139) показує, що кожне нове рівняння в системі добавляє 2 невідомих, причому існує лінійна залежність між татощо. В системі k-го порядку буде 2k+1 невідомих. Тому система рівнянь виду (9.140) з 2k+1 невідомими розв’язку не має.

Додаток А

Приклад розв’язку задачі аналізу на нерозрізнюваність

Базові статистичні ймовірнісні тести.Fips 140 - 1

Як базові рекомендується використовувати п'ять тестів:

• частотний (монобітний) тест;

• тест двох бітових серій;

• тест Поккера;

• тест серій (загальний);

• автокореляційний тест.