Задача 2.

Нехай Р=11 і Q=7. Побудувати пару (E_k, D_k) для RSA-перетворення, обґрунтувавши та вибравши один із випадкових ключів.

Розв’язок задачі:

Знаходимо модуль перетворення та значення функції Ойлера  (N)

Порівняння виду

.

запишемо у вигляді Діафантового рівняння

.

Вибравши випадково E_k =17 ключ, взаємопростий з функцією Ойлера, тобто (E_k,  (N)) = 1, маємо

.

Тепер подамо a/b у вигляді ланцюгового дробу:

;

60/17=3+9/17; 17/9=1+8/9; 9/8=1+1/8; 8/1=8+0.

Таким чином

.

Розраховуємо значення y=D_k, використовуючи співвідношення (1.59)

.

Знаходимо рекурентно значення а₂:

Підставивши значення а₂. в (1.10.12), маємо

.

Таким чином пара

складає RSA ключову пару.

Перевірка:

Підставивши значення ключів E_k =17та D_k = 53, маємо

.

Задача 10.

Нехай Р=11 і Q=7. Виберемо E_k=9 як випадковий ключ і побудуємо пару (E_k, D_k) для RSA ключів.

Розв’язок задачі:

Знаходимо модуль rsa перетворення та значення функції Ойлера:

Ключ D_k знайдемо із порівняння

,

далі зведемо вищенаведене порівняння до Діафантового рівняння

Знайдемо розклад ланцюгового дробу:

;

60/9=6+6/9; 9/6=1+3/6; 6/3=2+0.

Оскільки НСД , торозв’язку для пари ключів (E_k, D_k) немає.

1.8.2 Задачі для самостійного розв’язку

Задача 1. Побудувати пару (E_k,D_k) для RSA криптоалгоритму, якщо (значенняР і Q дивись у табл. 1.3).

Таблиця 1.3 – Значення Р і Q для задачі 1

n	1	2	3	4	5	6	7	8	9	10
Pп	29	11	11	11	23	7	29	17	19	19
Qп	11	17	23	13	17	23	7	7	7	11

де – номер за списком.

Якщо , то.

Задача 2. Розв’язати порівняння , якщо N = N_п (значення Р і Q дивись у табл. 1.4).

Таблиця 1.4 – Значення Р і Q для задачі 2

n	1	2	3	4	5	6	7	8	9	10
Nп	187	203	297	189	351	209	133	391	143	145

де - номер за списком.

Якщо , то.

Задача 1.

Нехай Р=11, Q=7, Е_k=37. Побудуйте ключову пару (E_k, D_k) для RSA-перетворення.

Розв’язок задачі:

Модуль перетворення має значення

N = P*Q = 11*7 = 77.

Розраховуємо значення функцій Ойлера

(N) = (P-1)(Q-1) = 10*6 =60 = 2² 3 5.

Для знаходження D_k ключа розв’яжемо порівняння

.

Подамо це порівняння у вигляді (1.58)

.

Підставимо значення  (N_j) та E_k маємо

.

Подамо а/b у вигляді ланцюгового дробу

;

60/37=1+23/37; 37/23=1+14/23; 23/14=1+9/14; 14/9=1+5/9; 9/5=1+4/5; 5/4=1+1/4; 4/1=4+0.

Це означає, що =6.

Тоді значення можна знайти з виразу

.

Підрахуємо коефіцієнти, а₀, а₁, а₂, а₃, а₄ та а₅.

Визначимо ключ розшифрування

y = D_k = (-1)⁶*13 = 13;

.

Перевірку здійснюємо підстановкою значень E_k та D_k в основне порівняння

.

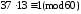Таким чином (E_k =37 та D_k= 13) є ключовою парою RSA-перетворення.

Задача 2.

Нехай Р=11 і Q=7. Побудувати пару (E_k, D_k) для RSA-перетворення, обґрунтувавши та вибравши один із випадкових ключів.

Розв’язок задачі:

Знаходимо модуль перетворення та значення функції Ойлера  (N)

Порівняння виду

.

запишемо у вигляді Діафантового рівняння

.

Вибравши випадково E_k =17 ключ, взаємопростий з функцією Ойлера, тобто (E_k,  (N)) = 1, маємо

.

Тепер подамо a/b у вигляді ланцюгового дробу:

;

60/17=3+9/17; 17/9=1+8/9; 9/8=1+1/8; 8/1=8+0.

Таким чином

.

Розраховуємо значення y=D_k, використовуючи співвідношення (1.59)

.

Знаходимо рекурентно значення а₂:

Підставивши значення а₂. в (1.10.12), маємо

.

Таким чином пара

складає RSA ключову пару.

Перевірка:

Підставивши значення ключів E_k =17та D_k = 53, маємо

.