10.3 Крипто перетворення нш в кільцях (rsa)

В 10.2, по суті , розглянуто етапи створення та певні властивості RSA направленого шифру. В цьому підрозділі розглянемо сутність RSA направленного шифру.

Алгоритм направленного шифрування.RSA криптоалгоритм є блоковим, у ньому повідомлення М розбивається на блоки М_i, з довжиною блоку (на сьогодні2048 біт мінімум), реально 2048, 3072 і більше бітів. Блок криптограма С_і обчислюється за правилом

, (10.2 1.49)

де – є відкритий ключ прямого перетворення,N – модуль перетворення є добутком виду

, (10.3 1.50)

де в свою чергу P, Q – великі прості, скоріше сильні, числа.

Якщо l_p є довжина простого числа Р, наприклад в бітах, а l_q – довжина простого числа Q, то довжина модуля N

. (10.4 1.51)

Розшифрування блока криптограми здійснюється за правилом:

, (10.5 1.52)

де D_к – є ключ зворотного перетворення, тобто розшифрування .

Однозначність розшифрування можна підтвердити, підставивши (10.5 1.52) в (10.2 1.49). В результаті отримаємо:

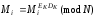. (10.6 1.53)

Оскільки ключова пара пов’язана між собою порівнянням:

, (10.7 1.54)

де є функцією Ойлера від модуляN

= .

Якщо (10.7 1.54) має єдине рішення, тобто існує єдина пара , то такий шифр є однозначним і при таких умовах RSA криптосистема забезпечує однозначне направлене шифрування.

Зазначимо, що з точки зору забезпечення максимально можливої крипто-стійкості прості числа P i Q мають бути сильними в широкому або вузькому значенні [7]. Так просте число Р вважатимемо сильним в широкому значенні, якщо

, (10.8 1.55)

де R – також велике просте число.

Аналогічно визначається і сильне в широкому значенні просте число Q.

Просте число Р вважається сильним у вузькому значенні, якщо містить в своєму канонічному розкладі велике просте числоR, Р+1 містить в своєму розкладі велике просте число S, а крім того R-1 містить в своєму розкладі велике число T.

Генерування асиметричної ключової пари. Система RSA відноситься до криптосистем з відкритими ключами. В цій системі ключі Е_kD_k, причому один з них має бути особистим, а другий – відкритим. Наприклад, Е_k – особистий, а D_k – відкритий, якщо вони використовуються для ЕЦП і навпаки, якщо використовуються для направленого шифрування.

Усі параметри (N,P,Q) також поділяються на 2 класи: N – відкритий, P,Q – конфіденційні (секретні).

Сутність забезпечення моделі взаємної недовіри – кожен користувач генерує ключі сам собі. Особистий ключ залишає в себе і забезпечує його строгу конфіденційність. Відкритий ключ розсилає всім користувачам, з якими він зв'язаний. Користувач також забезпечує цілісність і дійсність відкритих ключів.

Е_k, D_k – мають вибиратися з повної множини випадково, порівняно ймовір- но і незалежно, мають забезпечувати однозначну оборотність прямого та зворотного перетворення. Відповідним чином засвідчений відкритий ключ є сертифікатом (див. п. 1.1.1).

Значення Е_k, D_k для практичних використань мають задовольняти умову

,

де

.

Порівняння (1.54) можна звести до Діафантового рівняння:

ax+by=1. (10.9 1.56)

Це діафантове рівняння – нормоване, тому що справа коефіцієнт дорівнює 1; a, b – цілочисельні коефіцієнти, х, у – невідомі. Порівняння (10.7 1.54) можна подати у вигляді:

, (10.10 1.57)

k – деяке невідоме число.

Діафантове рівняння (10.9 1.56) має цілочисельне розв’язання, якщо a і b цілочисленні, і ,a і b взаємно прості. Подавши (10.10 1.57) у вигляді

, (10.11 1.58)

отримаємо а=(N), x=(k), b=E_k, y=D_k .

Якщо E_k сформувати випадково, то а та b – відомі числа, а х та y – невідомі, що підлягають визначенню.

Найбільш швидке розв’язання (10.11 1.58) дає застосування ланцюгових дробів, які дозволяють визначити х та у як

, (10.12 1.59)

де  – порядок ланцюгового дробу, a і b – параметри ланцюгового дробу.

Знаходимо параметри:

a/b подається у вигляді ланцюгового дробу

, (10.13 1.60)

μ - порядок ланцюгового дробу, перший коефіцієнт, у якого залишок дорівнює 0.

Значення (а₀,b₀) та (а₁,b₁) визначаються як

,

.

Значення (а₂,b₂), (а₃,b₃) і т.д. визначаються рекурентно відповідно до правил

. (10.14 1.61)

Середнє число ітерацій в (1.60), тобто , можна визначити як [16]

.

Попередня оцінка стійкості. В системі RSA крипто аналіз, метою якого є визначення особистого (таємного) ключа, наприклад Е_к ключа ключової пари (), деD_к є відкритий ключ, може бути здійснений таким чином:

1. Зловмисник отримує системні параметри (однакові для обох користувачів) та відкритий ключ Ек.

2. Використовуючи спеціальну крипто аналітичну систему здійснюється факторизація модуля , в результаті чого він визначає прості числата.

3. Розраховується значення функції Ойлера

.

4. Використовуючи методику, наведену в (1.49), здійснюється розв’язок порівняння .

Взагалі, найбільш простим методом крипто аналізу є підбір ключової пари (), тобто при відомихвизначаєтьсяDк.

Нехай має довжинутоді, якщо, то

.

Область існування для ключа 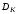можна визначити, як всі цілі числа, що не перевищуютьта є взаємно простими, тобто. Підбіріз повної множини є задачею, що набагато складніша, ніж алгоритм, заданий вище пп. 1-4.

Проведені дослідження підтвердили, що необхідний рівень стійкості в RSA забезпечується в тому випадку, якщо прості числа є сильними.

Покладемо, що як 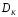використовуються прості числа, тоді справедливе таке:,,.

Використовуючи теорему Чебишева [17], визначимо кількість особистих ключів, як

. (10.15 1.62)

Приклад 1. Визначимо число простих 1024 бітних чисел

.

Щоб розв’язати цю задачу методом тотального перебору не вистачить енергії сонця.

Згідно з сучасними поглядами найбільш перспективними методами крипто аналізу є методи, що базуються на пп. 1-4, що розглянуті вище. При цьому найбільш складна задача факторизації модуля N вимагає найбільших ресурсів і суттєво залежить від використовуваного методу. На сьогодні відомо та апробовано такі методи факторизації:

• спробного поділу;

• -Полларда і -1 Полларда;

• Ленстра, з використанням еліптичних кривих ;

• квадратичне решето;

• загальне та спеціальні решета числового поля тощо

Згідно сучасних поглядів найбільш перспективним з точки зору мінімізації складності факторизації модуля є метод, що реалізований у вигляді загального решета числового поля [ ] та спеціального решета числового полях[ ]. В таблицях 10.2 та 10.3 показано результати, які отримано в світі при розв’язку задач факторизації.