12.2.2 Методи побудови загальних параметрів еліптичних кривих над полем .

Побудова загальних параметрів є в обчисленні параметрів кривої та визначенні її порядку. Аналіз джерел показав, що методи побудови загальних параметрів еліптичних кривих можна розділити на 2 групи:

методи, що ґрунтуються на побудові загальних параметрів вибраного порядку підгрупи базової точки, на основі якого обчислюються параметри кривої. Прикладом такого методу є метод „ комплексного множення ”[61 ];

методи обчислення порядку кривої, параметри якої вибрані випадково. До них відносяться методи Скуфа, SEA та „ Великих та малих кроків ” [134 – 135, 167 - 172].

Методи побудови на основі комплексного множення (вибраного порядку підгрупи базової точки) мають такі обмеження та недоліки:

порядок еліптичної кривої обчислюється попередньо та не є випадковим;

обмежене число кривих, що можуть використовуватися;

взаємна пов’язаність параметрів еліптичної кривої між собою;

значна складність обчислення кореня поліному. Причому максимально допустиме значення поліному не перевищує ;

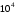обмеженість загальних параметрів значенням дискримінанти кривої.

З урахуванням вказаного метод комплексного множення використовувати не рекомендується.

Побудова загальних параметрів з використанням випадково генерованої кривої зводиться до перевірки параметрів кривої та обчисленню порядку кривої. Ці методи не мають вказаних недоліків, але вимагають значно більших обчислювальних ресурсів. Серед цих методів необхідно виділити метод Скуфа, що має поліноміальну складність. В подальшому цей метод був удосконалений Алкіном та Елкистом, що дозволило суттєво знизити складність його реалізації. Так, складність алгоритму Скуфа складає

, (1.44)

а складність удосконаленого SEA

(1.45) .

Проведені дослідження дозволяють зробити наступні висновки:

при виборі випадково вибраної еліптичної кривої забезпечується формування криптографічно стійких загальних параметрів;

алгоритм Скуфа забезпечує обчислення порядку будь-якої кривої як над простим так і над розширеним полем, але обчислювальна складність при цьому зростає зі збільшенням поліноміально;

алгоритм SEA має суттєво меншу складність обчислення порядку випадково генерованих еліптичних кривих.

Таким чином, на теперішній час розроблено та реалізовано метод побудови параметрів еліптичних кривих SEA, що задовольняє вимогам в частині криптографічної стійкості та має допустиму складність для кривих з порядком до .

12.2.3 Загальні параметри еліптичної кривої над полем

До загальних параметрів еліптичної кривої над полем відносяться наступні параметри:

Розмір поля , який визначає базове скінченне полеі є покажчиком базису, що використовується для подання елементів поля.

Бітовий рядок , якщо еліптична крива генерована випадково. В [62] наведено приклад того, як згенерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку(необов’язково).

Параметри таеліптичної кривої, які визначають рівняння еліптичної кривої, що використовується :.

Базова точка порядкуз координатамита.

Порядок базової точкипри умові, щота- просте число.

Кофактор взаємозв’язку порядку кривоїта порядку базової точкипричому( не обов¢язково, якщо це потрібно в базовій схемі).

Крива, тобто її параметри 1-6, ні в якому випадку не повинні вибиратись із переліку значень, що виключені із списку (не рекомендуються або заборонені).

Аналіз показує [32,44, 52], що на нинішній час розроблено та рекомендовано до використання ряд еліптичних кривих над полем . Так рекомендується використовувати полязі значенням. Особливістю цих значень є те, що дляможуть використовуватись тільки поліноми, що мають вигляд

f (x) =;

;

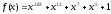; (1.46)

;

.

Необхідно вказати, що при використанні пентаномів, тобто поліномів з п’ятьма членами у порівнянні з трьома, збільшується складність крипто перетворень.

Для вказаних довжин порядок поля вибраний таким чином, щоб його довжина була у два рази більшою довжин ключів для симетричних шифрів. В цьому випадку забезпечується однаковий рівень стійкості симетричного шифру та крипто перетворень в групі точок еліптичних кривих.

В [62, 63] приведено 10 кривих над розширеним полем , перші 5 з них наведено в таблиці додатку А . Там же наведені значення порядку базової точки.

В [52] наведені параметри еліптичних кривих ,тадля еліптичних кривих в поліноміальному базисі () та оптимальному нормальному базисі ().

Таким чином, на теперішній час розроблено методи та засоби обчислення загальних параметрів. Існує можливість використання як уже сформованих та представлених у стандартах [32, 44, 52] параметрів, так і формування параметрів з використанням методів Скуфа та Сатоха[135].

Враховуючи складність формування загальних параметрів, на перших порах застосування стандарту ДСТУ ISO/IEC 15946 можна рекомендувати використовувати загальні параметри, що наведені в [32, 44, 52]. В подальшому повинні бути розроблені спеціальні програмно-апаратні комплекси, що призначені для формування загальних параметрів еліптичних кривих.