12.1.5 Порядок еліптичної кривої, що визначена над полем f(3m)

Слід E над полем F(pm) згідно з теоремою Хасе обмежений відрізком [–2√3^m, 2√3^m]. Згідно з теоремою Вотерхауза для t в діапазоні [–2√3^m, 2√3^m] існує еліптична крива E над F(3^m) зі слідом t.

Теорема 1.2 Вотерхауза. Нехай t є ціле, де | t | ≤ 2√3^m. Тоді існує еліптична крива, визначена над F(3^m) порядку 3^m+1 – t, якщо, і тільки якщо, дотримується одна з таких умов:

t є не кратне 3;

m є непарне і дотримується одне з наступного:

t = 0;

t² = 3^m+1 та p = 3. (1.30)

m є парне і виконується одна з умов:

t² = 4 3^m;

t² = 3^m 3;

t = 0.

Нехай E є еліптичною кривою над F(q), де q = p^m, і нехай n буде відносно простим числом для характеристики p функції F(q). Група n-кручення генерується двома точками, коли n – відносно просте число до p. E(F(q)) включає точку n-кручення G1, оскільки #E (F(q)) кратне простому n. Відзначимо, що цей факт не має на увазі E(F(q)) ⊃ E[n].

12.1.6. Параметри області еліптичної кривої

Параметри області еліптичної кривої над F(q)

Параметри еліптичної кривої над F(q), включаючи особливі випадки F(p) і F(2^m), повинні визначати:

– розмір поля q = p^m, який визначає базове скінченне поле F(q), де p повинно бути простим числом, і вказує на базис, що використовується для представлення елементів поля у випадку m > 1;

– якщо q = pm, причому p > 3, два елементи поля a і b у F(q), які визначають рівняння еліптичної кривої

E: y² = x³+ ax+ b;

⎯ якщо q = 2^m, то два елементи поля a і b у F(2^m), які визначають рівняння еліптичної кривої

E: y² + xy = x³ + ax² + b;

⎯ якщо q = 3^m, то два елементи поля a і b у F(3^m), які визначають рівняння еліптичної кривої

E: y² = x³ + ax² + b;

⎯ елементи поля x_G і y_G у F(q), які визначають базову точку G = (x_G, y_G) порядку n на еліптичній кривій E;

⎯ порядок n базової точки G;

⎯ значення кофактора h = #E(F(q))/n, якщо воно вимагається базовою схемою криптографічного перетворення.

12.1.7 Генерація ключів еліптичної кривої

Для заданого дійсного набору параметрів еліптичної кривої особистий ключ і відповідний відкритий ключ можуть бути генеровані таким чином:

Вибирається випадкове або псевдовипадкове ціле d на відрізку [2, n–2], яке має бути захищене від несанкціонованого розкриття й бути непередбачуваним.

Обчислюється точка

P = (x_P, y_P) = dG. (1.31)

Як ключова пара вибирається (P, d), де P – відкритий ключ, і d – особистий ключ.

У деяких застосуваннях відкритий ключ обчислюється як e G, за умови, що de = 1 mod n.

12.2 Основні методи побудування загальних параметрів еліптичних кривих

12.2.1 Загальні параметри еліптичних кривих над полями .

При викладенні питань побудування загальних параметрів еліптичних кривих будемо орієнтуватись на такі джерела як [50, 132 – 135, 167 - 171 ]

До загальних параметрів еліптичної кривої Е над полем 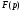відносяться наступні параметри:

Розмір поля , який визначає базове кінцеве пол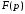е, деповинно бути простим числом.

Бітовий рядок , якщо еліптична крива генерована випадково. В [22] наведено приклад того, як генерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку(необов’язково).

Параметри таеліптичної кривої, які визначають рівняння еліптичної кривої, що використовується :.

Базова точка порядкуз координатамита.

Порядок базової точкиза умови, що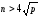та- просте число.

Кофактор взаємозв’язку порядку кривоїта порядку базової точки, причому.

Крива, тобто її параметри 1-6, ні в якому випадку не повинні вибиратись із переліку значень, що виключені із списку (не рекомендуються або заборонені).

Проведений аналіз дозволив сформулювати вимоги до розміру та властивостей загальних параметрів еліптичних кривих. Сутність цих вимог викладена нижче.

Порядок кривої порядокбазової точкиеліптичної кривої та модуль перетворенняє взаємозв’язаними

(1.38)

(1.39)

(1.40)

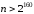(1.41)

Якщо підставити (2.1.7) та (2.1.8) в (2.1.6) одержимо

(1.42)

(1.43)

Співвідношення (1.40) – (1.43) дозволяють вибрати вказані загальні параметри ЕК.