ПРИКЛАДНА КРИПТОЛОГІЯ

ЛЕКЦІЯ №3(1.3)

Тема лекції

« МАТЕМАТИЧНІ ПЕРЕТВОРЕННЯ В КІЛЬЦЯХ ЗРІЗАНИХ ПОЛІНОМІВ ТА ПАРНІ ВІДОБРАЖЕННЯ ТОЧОК ЕЛІПТИЧНИХ КРИВИХ»

Навчальні питання

3.1 Основні властивості щодо еліптичних кривих

3.2 Криптографічне парне ( білінійне) відображення

3.3 Математичні основи методу направленого шифрування в кільцях поліномів.

• Математичні основи базового алгоритму NTRU

• Додаток А Питання для самоконтролю до першого розділу

Додаток Б Задачі для самостійного розв’язку до 1 розділу

• Додаток В Висновки та рекомендації за 1 розділ

Джерела, що рекомендуються до самостійної роботи

1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Підручник. Харків, ХНУРЕ, Форт, 2012 р., 878 с.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. Харків, ХНУРЕ, 2012 р.

3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

4. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний носій до підручника. Харків, ХНУРЕ, 2012 р.

5. Методичні вказівки до практичних занять з дисципліни «Прикладна криптологія» (друкований та електронній варіанти).

6. Методичні вказівки до лабораторних робіт з дисципліни «Прикладна криптологія» (друкований та електронній варіанти)

7. Плани проведення консультацій (друкований та електронній варіанти).

8.Навчальна програма з дисципліни «Прикладна криптологія».

9. Специфікація та завдання чотирьох модульних контролів – 4 тести.

10. Перелік питань та завдань до екзамену та екзаменаційні квитки.

11. Специфікація та завдання тесту залишкових знань.

3.1 Основні властивості щодо еліптичних кривих

У цьому підрозділі подані відомості щодо еліптичних кривих, які необхідні для асиметричних криптографічних перетворень у групі точок еліптичної кривої.

3.1.1 (1.4.1) Властивості еліптичних кривих

Порядок еліптичної кривої

Еліптична крива E над полем F(q) має бінарною операцією «+» складання точок E × E → E, для якої двом точкам Q₁, Q₂ на E може бути обчислена третя точка Q₁ + Q₂ на E. Еліптична крива E є абелевою групою щодо операції «+».

Число точок еліптичної кривої E (включаючи точку нескінченності 0_E) називається порядком E і позначається як #E(F(q)). Порядок кривої #E(F(q)) визначається згідно з теоремою Хасе [ ]:

q + 1 – 2√q ≤ #E (F(q)) ≤ q + 1 + 2√q. (1.28)

Ціле число t, визначене як t = q +1 – #E(F(q)), називається слідом. Теорема Хасе визначає межу по сліду.

Аномальні та супер сингулярні криві

Еліптична крива E, що визначена над полем F(q) з порядком #E(F(q))= p^m, де q = p^m, називається аномальною.

Еліптична крива E, визначена над F(q) зі слідом t, кратним p, називається супер сингулярною.

Аномальні криві вразливі до атак з використанням алгоритмів Аракі-Сатока , Смарта і Сімаіва [49].

Відносно супер сингулярних кривих існують вразливості, засновані на алгоритмах Фрея-Рюка та Менезіса-Окамото-Ванстона [47 - 49].

3.1.2 (1.6.1) Загальні параметри еліптичних кривих над полями

При викладенні питань побудування загальних параметрів еліптичних кривих будемо орієнтуватися на такі джерела, як [50, 132–135, 167–171].

До загальних параметрів еліптичної кривої Е над полем належать такі параметри:

Розмір поля , який визначає базове кінцеве поле, деповинно бути простим числом.

Бітовий рядок , якщо еліптична крива генерована випадково. У [22] наведено приклад того, як генерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації рядок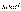(необов’язково).

Параметри таеліптичної кривої, які визначають рівняння еліптичної кривої, що використовується:.

Базова точка порядкуз координатамита.

Порядок базової точкиза умови, щота– просте число.

Кофактор взаємозв’язку порядку кривоїта порядку базової точки, причому.

Крива, тобто її параметри 1–6, ні в якому разі не повинні вибиратись із переліку значень, що виключені зі списку (не рекомендуються або заборонені).

Проведений аналіз дозволив сформулювати вимоги до розміру та властивостей загальних параметрів еліптичних кривих. Сутність цих вимог викладена нижче.

Порядок кривої порядокбазової точкиеліптичної кривої та модуль перетвореннявзаємопов’язані:

(1.38)

(1.39)

(1.40)

(1.41)

В цілому маємо:

(1.42)

(1.43)

Співвідношення (1.40)–(1.43) дозволяють вибрати вказані загальні параметри ЕК.