Случайные процессы и их вероятностные характеристики

Классификация всех процессов на пальцах (не строго) [5]. Строгие определения будут дальше.

ПРОЦЕССЫ
детерминированные			хаотические		случайные
периодические	непериодические				стационарные		нестационарные
	квазипериодические	переходные		эргодические		не эргодические	разные типы

С практической точки зрения решение о случайности или детерминированности процесса основывается на способности воспроизвести процесс в ходе контролируемого эксперимента. Если это приводит к одним и тем же результатам – то процесс считается детерминированным.

Детерминированные процессы – это процессы, которые можно описать математическими формулами (т.е. мы можем определить положение системы в любой момент времени с разумной точностью). Например: движение спутника на околоземной орбите, измерение температуры воды при нагревании.

А процессы, такие как высота волн при небольшом (и большом) шторме, напряжение в нашей электросети, изменение численности жителей в Харькове с течением времени не являются детерминированными – точное положение системы в таких процессах точно определить невозможно. Для описания этих процессов требуются вероятностные понятия и статистические характеристики.

Есть еще третий вид процессов - хаотические. С одной стороны – детерминированные. Но очень нелинейные, с сильной зависимостью от начальных условий. В реальности начальные условия точно повторить нельзя, и поведение системы через некоторое время становится непредсказуемым. На выходе такие системы имеют случайные характеристики и к ним требуются вероятностные подходы.

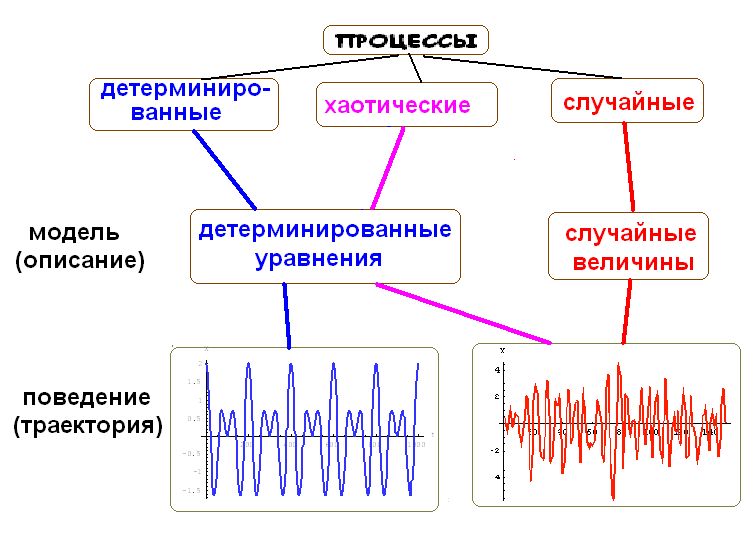
Кратко охарактеризуем основные виды процессов.

Детерминированные процессы.

Периодическиепредставимы какX( t )=X( t+T )и разлагаются в ряд Фурье X(t)=

с соизмеримыми частотами (отношениеявляется рациональным числом).

Например, радиосигнал с определённой частотой.

Приближённо такими процессами являются: напряжение на выходе электрического генератора; вибрация двигателя внутреннего сгорания.

Если в спектре присутствуют частоты, отношения которых является иррациональным числом, то процесс называетсяквазипериодическим. К таким процессам относится вибрация многомоторного самолета, в котором двигатели не синхронизированы.

Все остальные процессы считаются переходными(система не вышла на установившийся режим)

Примеры.

Температура воды в чайнике после отключения питания:

Затухание маятника после толчка:

Напряжение в тросе, который разрывается:

Случайные процессы

Теорией случайных процессов (CП) называется математическая наука, изучающая случайные явления в динамике их развития.

Стационарные– очень грубо говоря, характеристики этих процессов не зависят от их расположения на временной оси. Для исследования хорошо развит матаппарат. Например: давление газа в газопроводе, колебания напряжения в сети.

Эргодическиепроцессы –такие стационарные процессы, когда по одной временной реализации процесса можно найти характеристики процесса. На практике, практически все стационарные процессы оказываются эргодическими (или сводятся к ним)

У нестационарныхпроцессов все свойства существенно зависят от времени (например, число студентов, проходящих через проходную ХИРЭ в единицу времени).

Определение СП [1,3]

Случайные процессы являются матмоделями для описания случайных явлений, развивающихся во времени. При этом предполагается, что состояние в текущий момент времени есть случайная величина Пространство элементарных событийпредполагается измеримым (т.е. на нём определена-алгебра его подмножеств. Предполагается, что на измеримом пространствезадана вероятностная мераР, то есть для любого событияопределена его вероятностьР(А). Таким образом задано вероятностное пространство)

Случайный процесс есть семейство случайных величин (СВ) , определённых на, где под параметромt понимается время и .

Пусть - фиксированный момент. Случайная величинаназывается сечением случайного процесса в точке.

СП можно рассматривать как совокупность случайных величин, зависящих от параметра t .Процесс может быть действительным или комплексным в зависимости от вида СВ

Мы фиксировали время. А теперь пусть - фиксируемый результат испытания. Тогданеслучайная функция (в которую превращается процесс в результате испытания) называется реализацией (траекторией, выборочной функцией) СП.С реализациями мы чаще всего имеем дело на практике. Таким образом, СП можно рассматривать как совокупность всех возможных его реализаций.

СП классифицируют в зависимости от непрерывности или дискретности и Т:

1) СП называется процессом с дискретным временем(или случайной последовательностью) если система, в которой он протекает, может менять своё состояние в дискретные моменты времени.

Например: некто накупил всяких лотерейных билетов. Выигрыши происходят в определённые дни. Случайный процесс - число билетов, выигравших до момента времениt.

2) СП называется процессом с непрерывным временем, если переходы системы могут происходить в любой момент.

Например: техническое устройство может иметь три состояния : работает нормально, работает с перебоями, ремонтируется. Случайный процесс - состояние устройства в момент времениt.

3) СП называется процессом с дискретными состояниями, если в любой момент времени множество его состояний конечно или счётно (если любое его сечение – дискретная СВ).

4) СП называется процессом с непрерывными состояниями, если множество его состояний несчётно (если любое его сечение – непрерывная или смешанная СВ)..