ВП_экзамен2012 / lectlons / lectlons / spektr

Спектральное представление ССП.

Спектры детерминированных сигналов.

Сигнал - функция, переносящая информацию.

Среди разнообразных систем ортогональных функций, которые могут быть использованы в качестве базиса для представления сигналов, исключительное место занимают гармонические функции потому, что

1. гармонические сигналы инвариантны относительно линейных преобразований,

2. техника генерирования этих сигналов относительно проста.

Если сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение сигнала. Гармонические компоненты образуют его спектр.

Разложение периодических сигналов в ряд Фурье.

Периодический сигнал , .

, где - ортонормированный базис, -коэффициенты.

Основная частота:.

Угловая частота:.

Циклическая частота: Гц.

Ряд Фурье для сигнала:

В общем случае сигнал содержит не зависящие от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами , кратными основной частоте последовательности.

У каждой гармоники своя амплитуда.

Ряд Фурье в комплексной форме.

Базисные функции - экспоненты с мнимыми показателями.

, ( * )

( ** )

Спектр сигнала s(t) содержит компоненты и на отрицательной полуоси частот, причем ( для действительных сигналов они совпадают ).

Отрицательная частота - понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел.

Преобразование Фурье.

Для непериодических процессов устремляем и переходим к интегралу. Что происходит? Частоты соседних гармоник и окажутся сколь угодно близкими и дискретную частоту можно заменить непрерывной .

Прямое преобразование Фурье имеет вид:

Это преобразование существует, если существует

Тогда обратное преобразование Фурье будет иметь вид:

, где S(w) - спектр сигнала.

Преобразование Фурье обладает следующими основными свойствами:

1. линейность ;

2. если сигнал 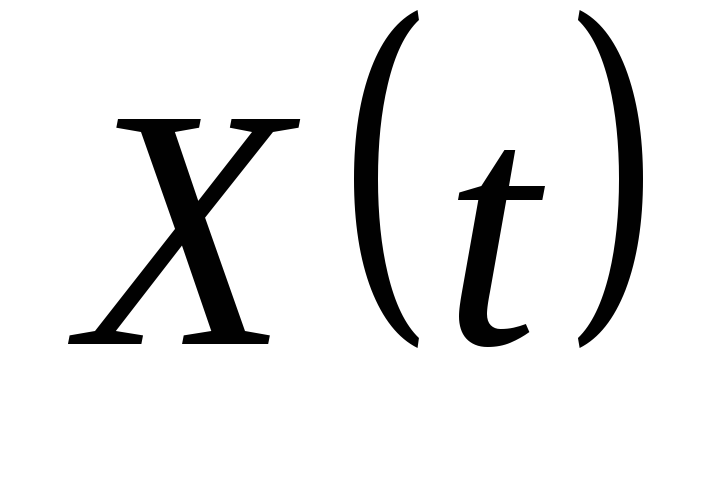- действительный, то 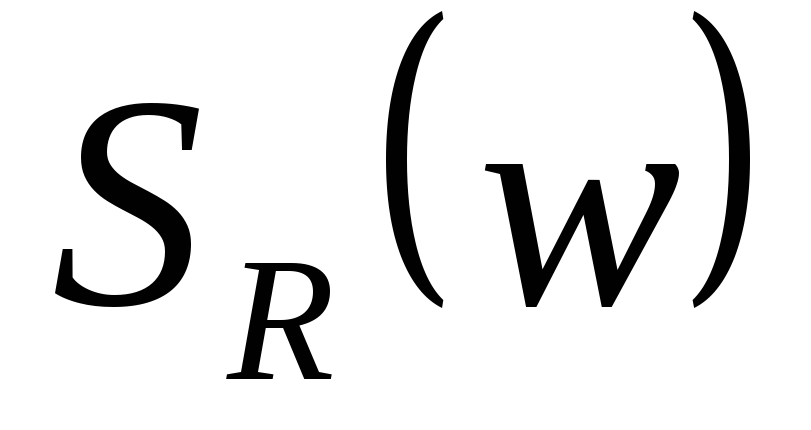-является четной, а 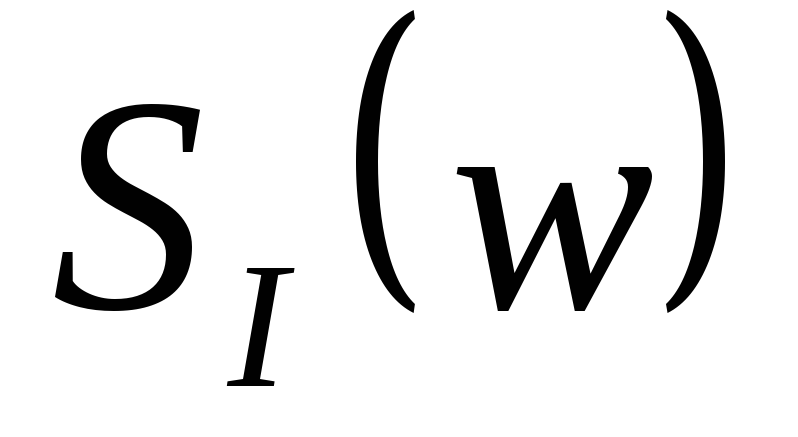-нечетной функцией;

3. для смещенного во времени сигнала ;

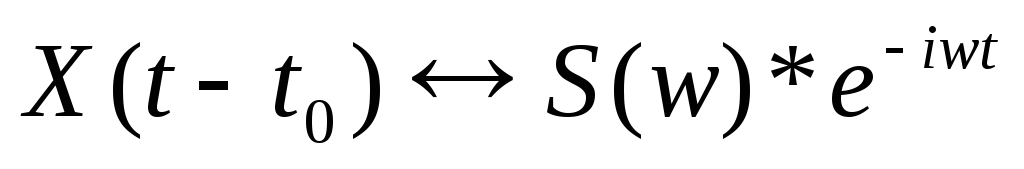4. при изменении масштаба времени .

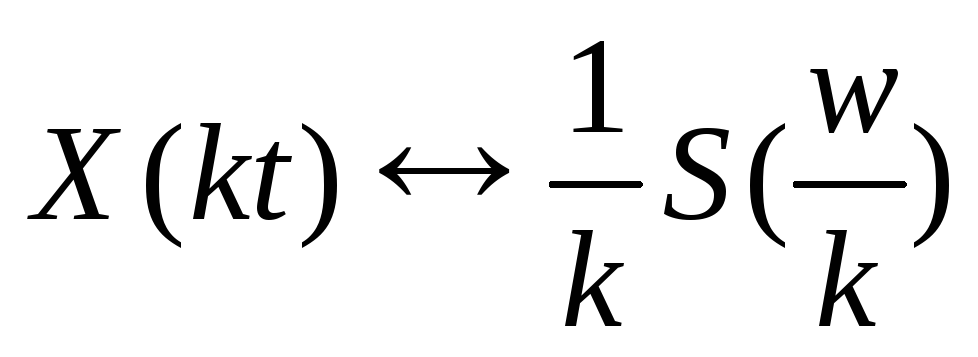Спектральное разложение случайных стационарных процессов.

Если периодична , то с вероятностью 1 периодична реализация и наоборот.

Корреляционную функцию можно разложить в ряд Фурье:

,

( * )

Теорема.

Если - случайный стационарный периодический процесс и его корреляционная функция представлена в виде разложения в ряд Фурье ( * ), то сам процесс тоже может быть представлен в виде ряда:

где - случайные величины такие, что:

,

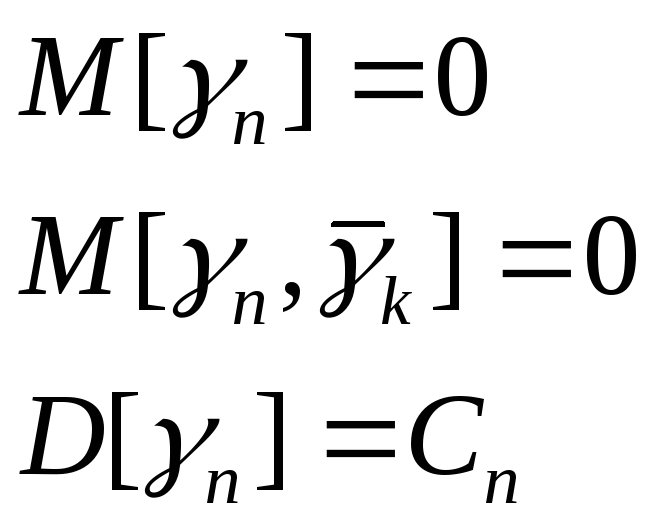
Каноническое разложение:

Спектральная плотность cтационарныx процессов. .

.

Для удобства говорим о центрированных случайных процессах.

Периодический процесс (периодическая корреляционная функция).

, ,

где

Так как корреляционная функция - четная функция, то есть , для центрированного процесса - действительная, то мы можем перейти к косинус преобразованиям Фурье:

Дисперсия стационарного периодического процесса:

Дисперсия стационарного случайного процесса, представленная спектральным разложением, равна сумме всех дисперсий гармоник его спектрального разложения.

Непериодический процесс:

,

-интервал между соседними частотами.

W(w) -спектральная плотность стационарного случайного процесса, плотность распределения дисперсий по непрерывным частотам.

Она же - спектр мощности, спектральная плотность мощности, энергетический спектр. W(w) характеризует удельную меру мощности.

Опять вернемся к общему преобразованию Фурье.

- формулы Винера-Хинчина

Функция корреляции и спектр плотности связаны между собой преобразованиями Фурье.

Еще раз о физическом смысле W(w).

- распределение энергии по частоте.

- средняя мощность флуктуации процесса.

- односторонний спектр мощности.

Свойства спектральной плотности.

1. Если - вещественный, то - четная функция.

2. Спектральная плотность - неотрицательная функция, то есть: .

3. Если дисперсия ограничена, то W(w) - интегрируемая функция:

Примеры.

1. Спектр плотности действительного случайного процесса :

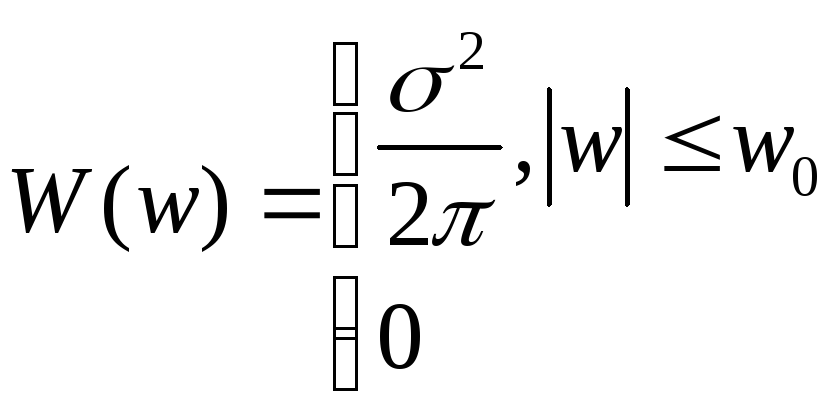
Найти: .

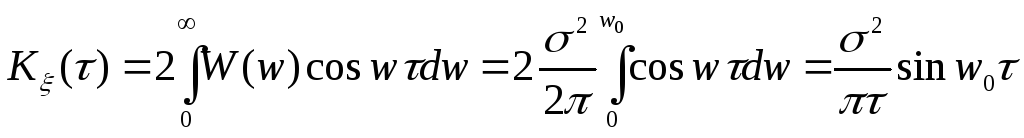
В точках , то есть сечения ,- некоррелируемы.

2. Существует ли стационарный случайный процесс, имеющий корреляционную функцию вида:

?

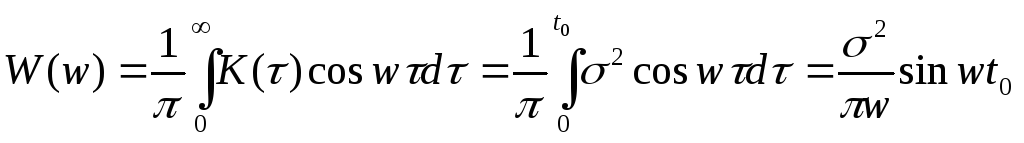
Эта корреляционная функция не может быть корреляционной функцией стационарного процесса, так как спектральная плотность должна быть больше 0, а в данном случае есть синус, который приводит к минусу.

Белый шум.

Белый шум – случайный процесс с постоянной спектральной плотностью для всех частот, то есть . Для белого шума характерно равномерное распределение энергии по всем частотам. Реально он не существует.

Корреляционная функция белого шума имеет вид:

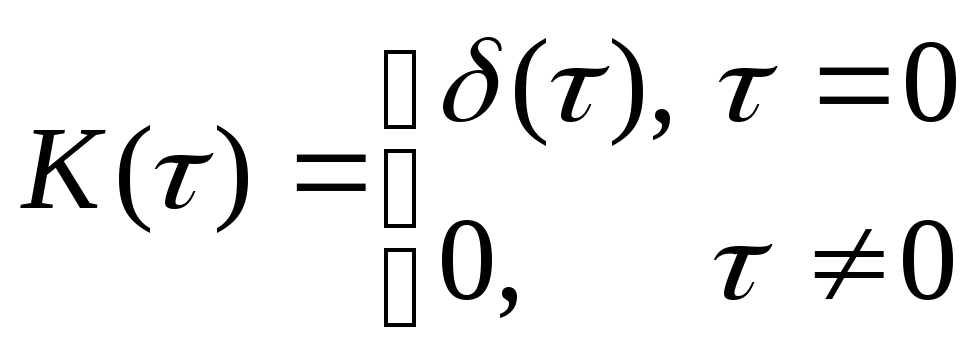
Интервал корреляции.

Многие случайные процессы обладают свойством: их функция корреляции стремится к 0 с увеличением временного сдвига .

Чем быстрее убывает , тем меньше оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающие момента времени.

Числовой характеристикой, служащей для оценки скорости изменения реализации случайного процесса, является интервал корреляции :

Если известна информация о поведении какой-либо реализации в прошлом, то возможен вероятностный прогноз на время .

Пример.

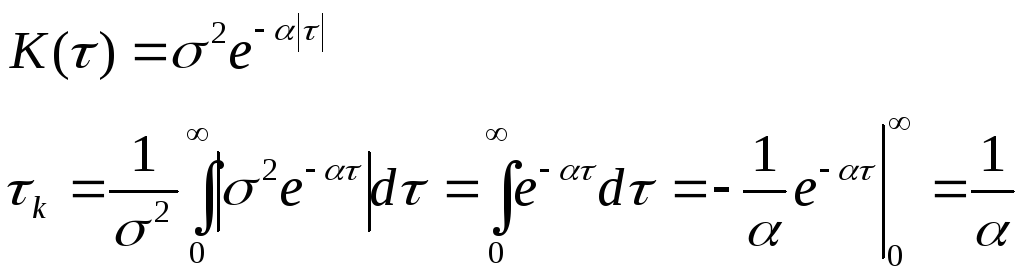
характеризует скорость уменьшения корреляции между сечениями.

Эффективная ширина спектра.

Заменим мысленно стационарный случайный процесс процесс другим, у которого спектральная плотность мощности постоянна, ,так, что

Вне пределов эффективной ширины спектра спектральную плотность мощности считают равной 0.

- есть постоянное число порядка 1.

Чем меньше интервал корреляции, тем шире его спектр.

6