4.2 Числовые поля
4.2.1 Поле рациональных чисел
В
кольце целых чисел
 операция деления не выполняется. Это
послужило причиной расширения кольца
целых чисел до поля рациональных чисел.
При расширении кольца целых чисел
операция деления не выполняется. Это
послужило причиной расширения кольца
целых чисел до поля рациональных чисел.
При расширении кольца целых чисел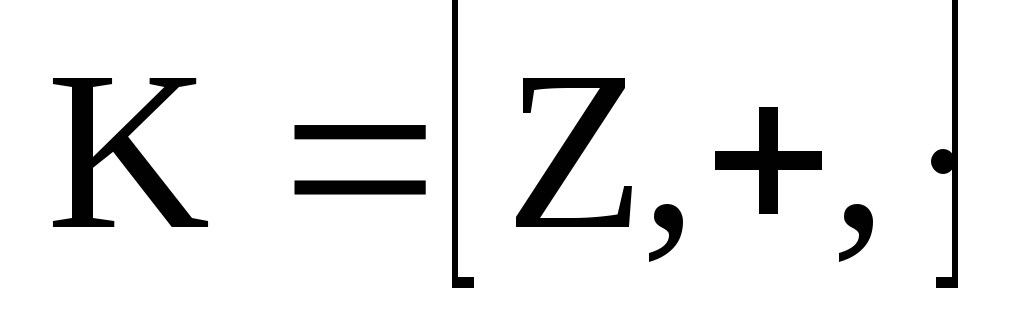 до поля рациональных чисел
до поля рациональных чисел руководствовались следующими требованиями:
руководствовались следующими требованиями:
Кольцо
целых чисел
 должно быть подкольцом кольца рациональных
чисел
должно быть подкольцом кольца рациональных
чисел .
.
В
кольце
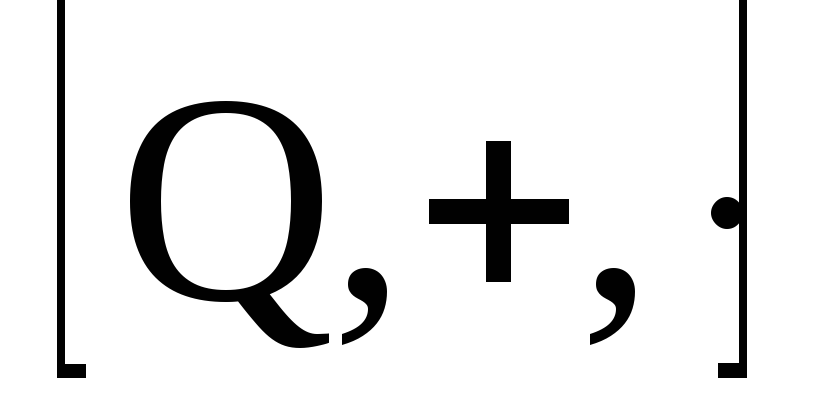 должна выполняться операция деления,
кроме деления на нуль. Это означает,
что кольцо
должна выполняться операция деления,
кроме деления на нуль. Это означает,
что кольцо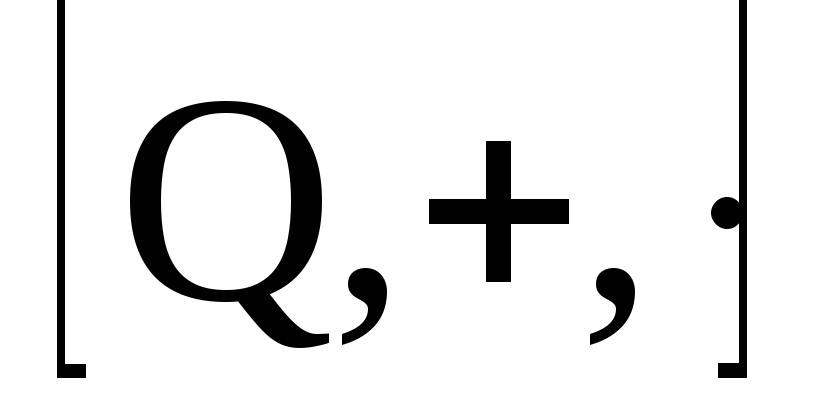 должно быть полем.
должно быть полем.
Среди
полей являющихся расширением кольца
 поле
поле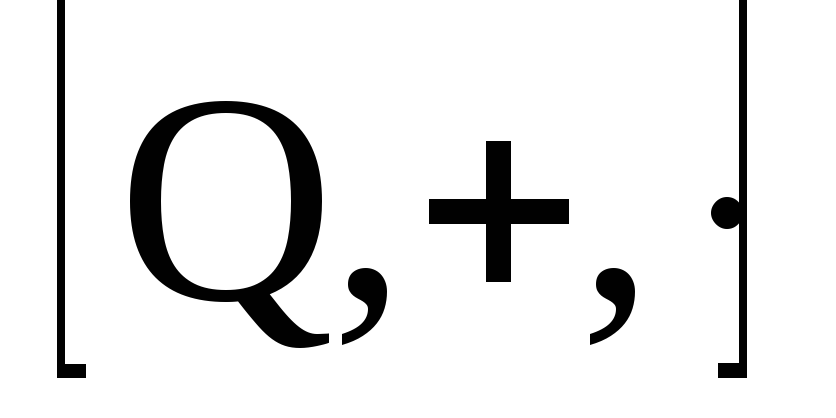 должно быть минимальным.
должно быть минимальным.
Определение. Полем
рациональных чисел
 называется минимальное поле, являющееся
расширением кольца целых чисел
называется минимальное поле, являющееся
расширением кольца целых чисел .
.
Можно показать,
что поле рациональных чисел существует,
и притом (с точностью до изоморфизма)
единственно.
Элементами
поля рациональных чисел являются,
естественно, рациональные числа
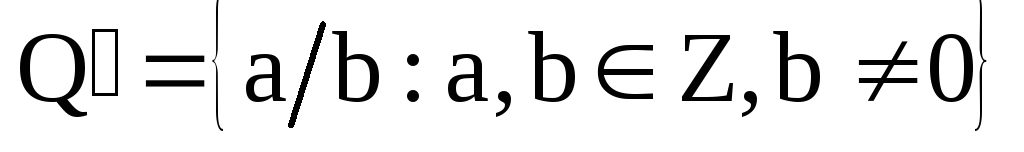 .
Для рациональных чисел
.
Для рациональных чисел ,
как для элементов поля, верны все правила
действия над частными (дробями).
,
как для элементов поля, верны все правила
действия над частными (дробями).
Теорема. Поле
рациональных чисел
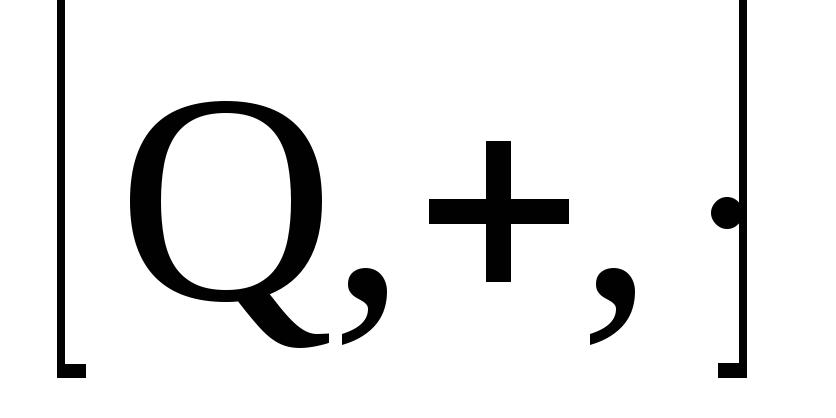 можно упорядочить.
можно упорядочить.
Доказательство. Условимся
считать рациональное число
 ,
где
,
где ,
положительным, тогда и только тогда,
когда оба числа
,
положительным, тогда и только тогда,
когда оба числа одновременно положительные или
отрицательные. Другими словами, число
одновременно положительные или
отрицательные. Другими словами, число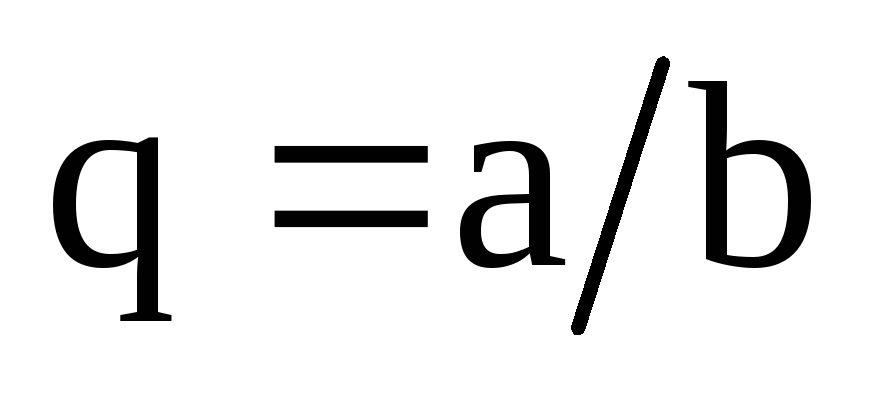 будем считать положительным тогда и
только тогда, когда число
будем считать положительным тогда и
только тогда, когда число – положительное.
– положительное.
Рациональное
число
 будем считать меньше рационального
числа
будем считать меньше рационального
числа ,
а рациональное число
,
а рациональное число – больше рационального числа
– больше рационального числа и писать
и писать в том и только том случае, если
в том и только том случае, если – положительное рациональное число.
Ясно, что положительные числа больше
0, а отрицательные–меньше 0. Легко
проверить, что так определенное отношение
– положительное рациональное число.
Ясно, что положительные числа больше
0, а отрицательные–меньше 0. Легко
проверить, что так определенное отношение – «меньше» является совершенным
отношением строгого порядка. Таким
образом. Поле рациональных чисел
– «меньше» является совершенным
отношением строгого порядка. Таким
образом. Поле рациональных чисел с помощью отношения
с помощью отношения – «меньше» линейно упорядочивается.
– «меньше» линейно упорядочивается.


 операция деления не выполняется. Это
послужило причиной расширения кольца
целых чисел до поля рациональных чисел.
При расширении кольца целых чисел
операция деления не выполняется. Это
послужило причиной расширения кольца
целых чисел до поля рациональных чисел.
При расширении кольца целых чисел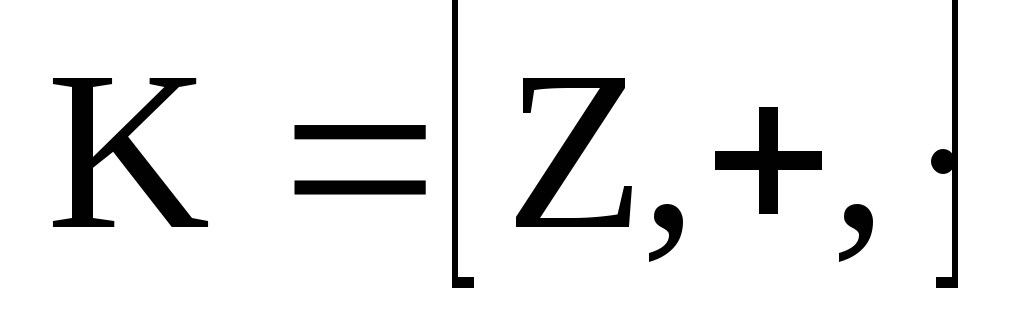 до поля рациональных чисел
до поля рациональных чисел руководствовались следующими требованиями:
руководствовались следующими требованиями: должно быть подкольцом кольца рациональных
чисел
должно быть подкольцом кольца рациональных
чисел .
.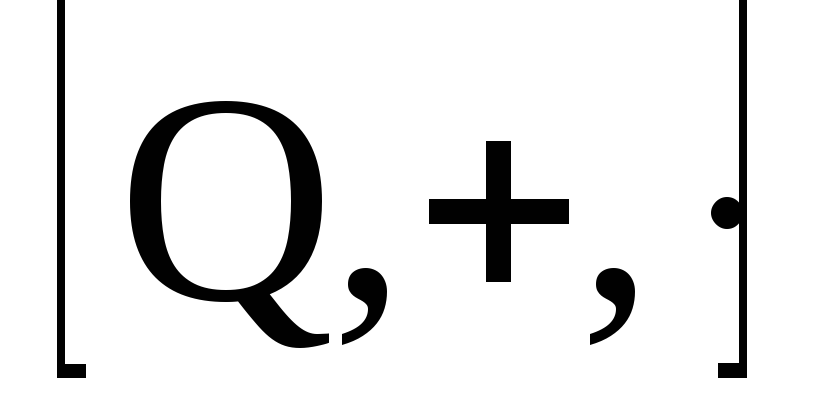 должна выполняться операция деления,
кроме деления на нуль. Это означает,
что кольцо
должна выполняться операция деления,
кроме деления на нуль. Это означает,
что кольцо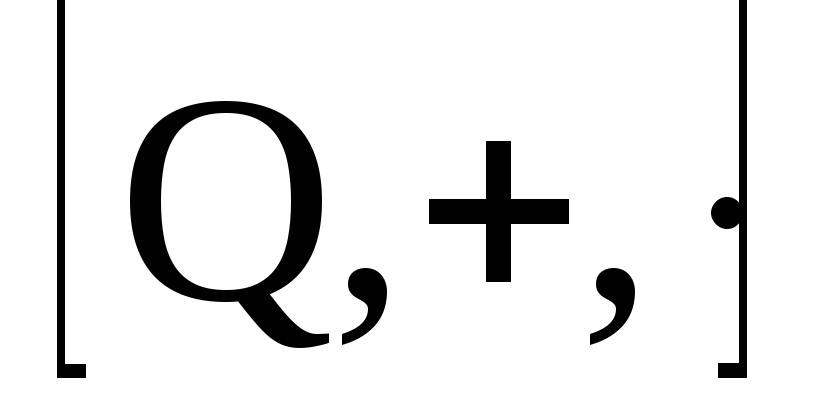 должно быть полем.
должно быть полем. поле
поле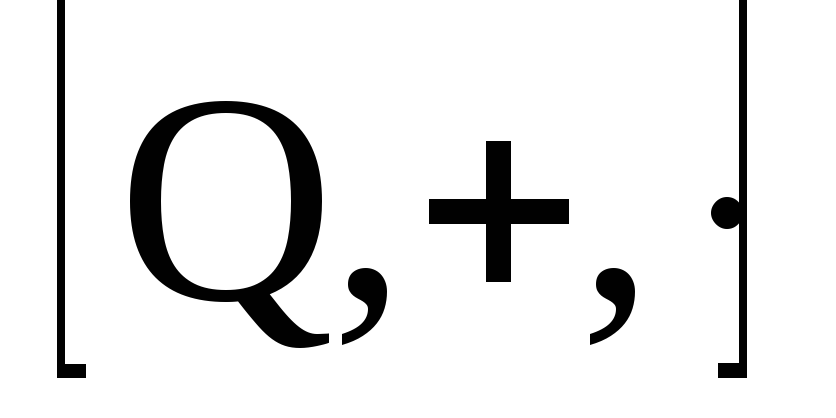 должно быть минимальным.
должно быть минимальным. называется минимальное поле, являющееся
расширением кольца целых чисел
называется минимальное поле, являющееся
расширением кольца целых чисел .
.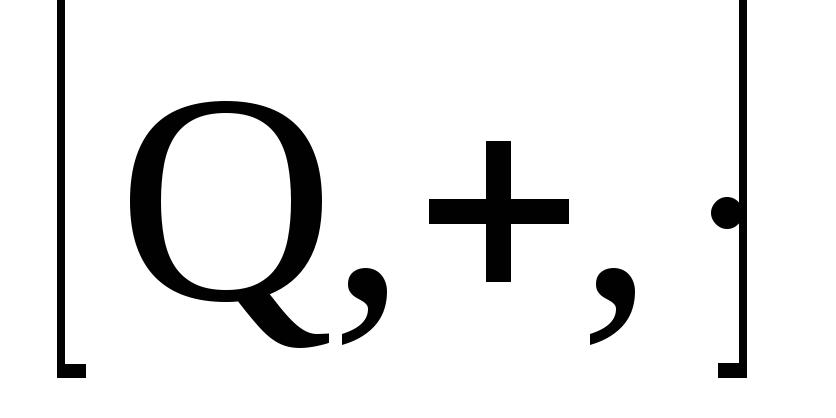 можно упорядочить.
можно упорядочить. с помощью отношения
с помощью отношения