3.3.5 Характеристика кольца с единицей

Выясним какие идеалы есть в простейшем кольце – кольце целых чисел 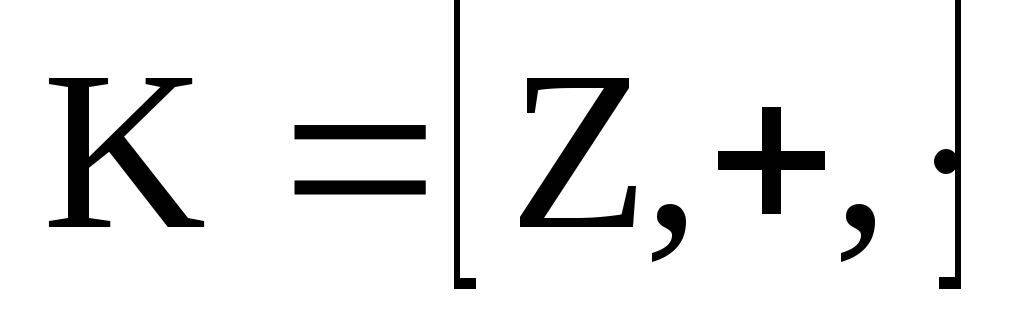. Любое целое числопорождает главный идеал. Такими идеалами исчерпывается множество всех идеалов кольца, поскольку справедлива следующая теорема.

Теорема. Каждый идеал кольца целых чисел является главным идеалом.

Доказательство. Пусть – некоторый идеал кольца– целых чисел. Если– нулевой идеал, то. Если же в идеалесодержится число, то в нем содержится также и число. Одно из чиселилиположительное, поэтому в идеалесодержатся натуральные числа. Пусть– наименьшее из натуральных чисел, содержащихся в. Тогда

(3.72)

и, следовательно, .

Докажем и обратное включение. Действительно, пусть – произвольный элемент из идеалакольца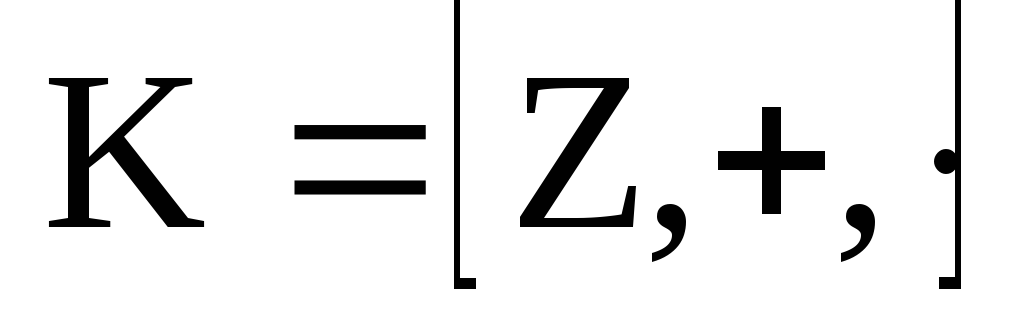. Разделивна, получимПосколькуи, то. Отсюда и из условияследует, что, так как в противном случаене было бы наименьшим среди натуральных чисел, содержащихся в идеале. Таким образом,и, следовательно,. Таким образом

Пусть – кольцо целых чисел, а– произвольное кольцо с единицей. Рассмотрим отображение

(3.73)

вида

Очевидно, что отображение является гомоморфизмом кольца целых чиселв кольцо.

Множество является подкольцом кольцаи состоит из всех целых кратныхединичного элемента. Это подкольцобудем называтьподкольцом, порожденным единичным элементом кольца. В этом случае отображениеявляется гомоморфизмом кольца целых чиселна подкольцокольца.

Поэтому по теореме о гомоморфизме колец, подкольцо изоморфно фактор-кольцу, где. Поскольку в кольце целых чиселкаждый идеалглавный, то, где– некоторое неотрицательное число. Возможны два случая :

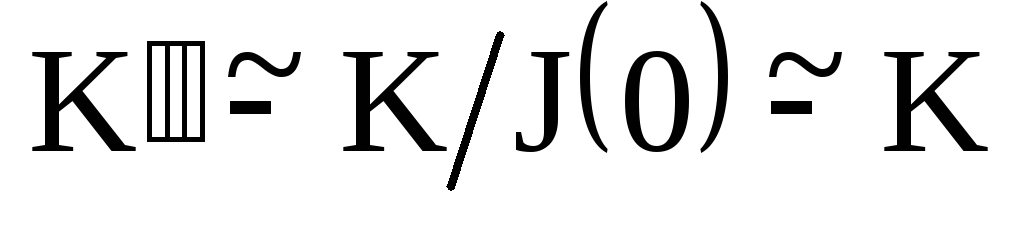• . Тогда т.е. подкольцоизоморфно кольцу целых чисел;

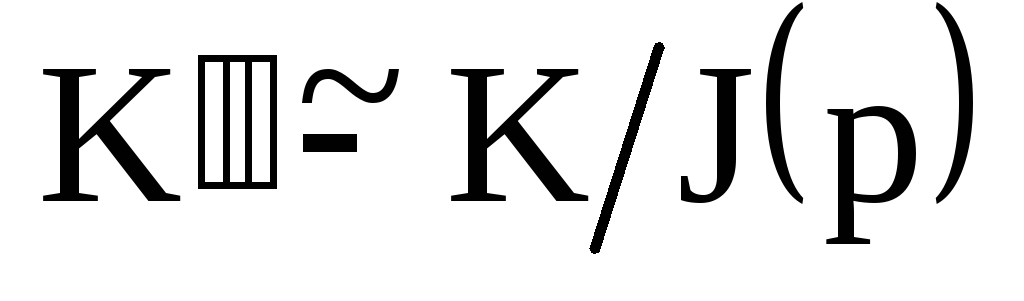• . Тогда т.е. подкольцоизоморфно кольцу классов вычетов по модулю.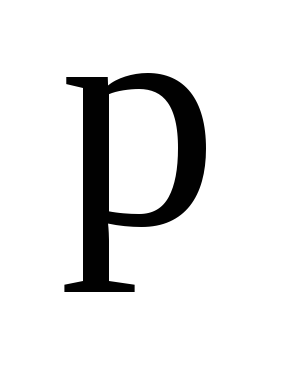

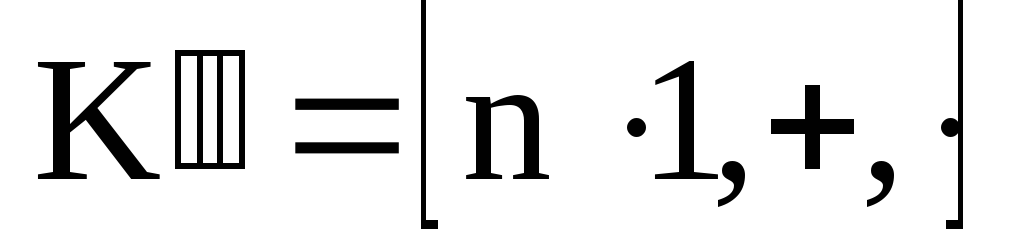Следовательно, в любом кольце с единицейподкольцопорожденное элементом, изоморфно или кольцу целых чиселили кольцу классов вычетов по модулю :, где– некоторое натуральное число. Пусть– некоторое кольцо с единицей.

Определение. Характеристикой кольца называется порядок подгруппы, порожденной единицей в аддитивной группекольца.

Замечание. В случае, если группа порожденная единицей кольца, бесконечна, принято говорить, что кольцо имеет характеристику нуль, а не бесконечность. Числовые кольца ,,,имеют характеристику нуль, а кольцо классов вычетов по модулю:имеет характеристику.

Определение. Кольцо имеет характеристику 0, если его подкольцо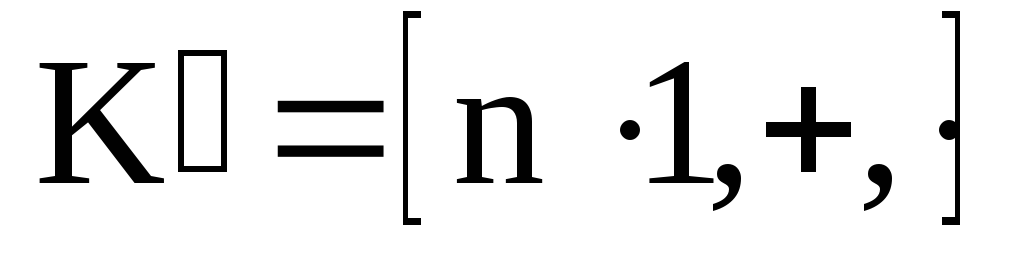порожденное единичным элементом, изоморфно кольцу целых чисел.

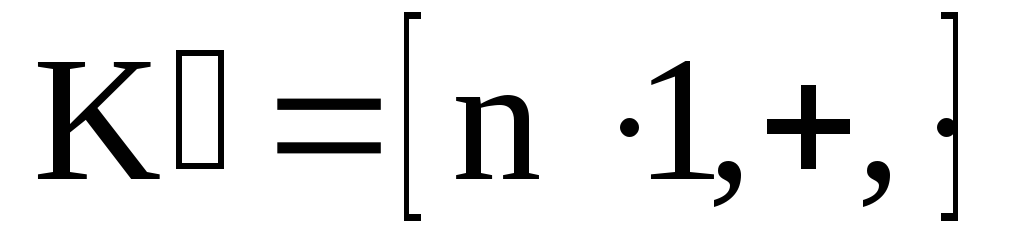Определение. Кольцо имеет характеристикуесли его подкольцоизоморфно кольцу классов вычетов по модулю.

По определению, кольцо целых чисел имеет характеристику 0, а кольцо– классов вычетов по модулюимеет характеристику.

Замечание. Наряду с высказыванием «кольцо имеет характеристику 0 (или )» применяют также высказывания «характеристика кольцаравна 0 (или р)», «является кольцом характеристики 0 (или р)»

Теорема. Если кольцо имеет характеристику 0, то только при; если же имеет характеристику, тои нет такого натурального числа, что.

Доказательство. Пусть — кольцо характеристики 0 Тогда существует изоморфное отображение подкольцана кольцо – целых чисел. Поскольку по теореме 6 при гомоморфизме (в частности, изоморфизме) кольцана кольцо , то . Поэтому только при, ибо если , то , по теореме 6, равно 0, т. е. .

Предположим, что — кольцо характеристики р. Тогда существует изоморфное отображение кольца на подкольцо. По теореме 6, , где , и поэтому . Посколькуи по теореме 6 , то . Если , то , а поэтому и , так как в противном случае отображение было бы гомоморфизмом, а не изоморфизмом.

Справедлива также и обратная теорема.

Теорема. Если в кольце с единицейравенствосправедливо только при, тоимеет характеристику 0; если в кольце справедливо равенствои нет такого натурального, что, тоимеет характеристику р.

Доказательство. Рассмотрим гомоморфизм , для которого . По теореме о гомоморфизмах колец , где — ядро гомоморфизма . Если в равенствосправедливо только при, то при гомоморфизме в нуль кольца отображается только 0 кольца ; поэтому и, следовательно,, т. е. . Если в кольце справедливо равенствои нет такого натурального , что , то при гомоморфизме в ноль кольца отображаются все целые кратныечислаи только они; поэтомуи .

Из теорем 9 и 10 вытекает следующее определение.

Определение. Характеристикой кольца с единицейназывают число 0, если только при ; характеристикой кольца называют натуральное число, еслии нет такого натурального числа, что.

Все числовые кольца с единицей, очевидно, имеют характеристику 0. Каждое конечное кольцо с единицейявляется кольцом ненулевой характеристики. Действительно, если кольцоконечно, то среди всех целых положительных кратных единичного элементаобязательно будут кратные, равные между собой, так как в противном случае кольцобыло бы бесконечным. Пусть., где и – некоторые натуральные числа, причем . Тогда и, следовательно, является кольцом ненулевой характеристики.

Каждое натуральное число является характеристикой некоторого кольца с единицей:является характеристикой кольца. Докажем теперь две теоремы, которые характеризуют свойства колец характеристики 0 и характеристики .

Теорема. Если является областью целостности характеристики 0, то

.

Доказательство. Пусть – произвольно выбранный, отличный от 0, элемент из и – любое натуральное число. Тогда

.

Предположим, что , тогда и . Поскольку в нет делителей нуля и по условию теоремы , то из равенства вытекает, что, чего не может быть. Следовательно,. предположение, что, неправильное. Таким образом, для любого натурального имеем. При любом целом отрицательномтакже, ибо если бы элементкольца был равен нулю, то и противоположный ему элемент также был бы равен нулю, чего по доказанному выше не может быть.

Теорема. Если – кольцо характеристики, то

.

Доказательство. Действительно,

.

Эти кольца получили название колец главных идеалов. Пусть – кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:

Определение.  Если для элементов кольца целостностив кольце существует такой элемент, что, то говорят, что элементделится на, и пишут илиделит, и пишут , или.

Из определения делимости двух элементов вытекают следующие свойства делимости в кольце целостности:

1. 

2. 

3. 

4. 

Эти свойства являются распространением на кольцо целостности соответствующих свойств делимости в кольце целых чисел.

5. Каждый элемент делится на любой делительединицы. Действительно, если– делитель единицы, то и– также делитель единицы, а это означает, что, тогдаи, следовательно,.

6. Если делится на, тоделится и на, где– любой делитель единицы.

Действительно, из равенства следует равенствои, следовательно,.

7. Каждый элемент из делителей и, где– любой делитель единицы, является делителем и другого.

Действительно, из равенства следует равенство, а из равенства– равенство. Следовательно, если, то, и наоборот.

В дальнейшем будем рассматривать элементы кольца целостности , отличные от нуля.

Определение. Элементы кольца целостностиназываютсяассоциированными, если каждый из них является делителем другого:

. (55)

Из равенства (55) следует, что . Отсюда, сократив обе части полученного равенства на, получаем. Следовательно,иявляются делителями единицы. Таким образом, еслии– ассоциированные элементы, то, где– некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы, элементыиассоциированные между собой, поскольку.

Определение. Элементы кольца целостностиназываютсяассоциированными, если , где– некоторый делитель единицы.

Пример. В кольце целых чисел ассоциированными являются пары чисел.

Если иассоциированные элементы кольца целостности, то. Отсюда следует, что– главный идеал, порожденный элементомявляется подмножеством– главного идеала, порожденного элементоми наоборот:

Это означает, что два ассоциированных элемента , кольца целостностипорождают один и тот же главный идеал.

Пусть – произвольные элементы кольца целостности.

Определение. Элемент называется общим делителем элементови, если каждый из этих элементов делится на.

По свойству 5 все делители единицы кольца целостностиявляются общими делителями элементови. Но у элементовимогут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называютнаибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности нет отношения порядка. Однако можно ввести и другое определение НОД двух чисели, а именно: НОД двух чиселиназывается такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности.

Определение. Наибольшим общим делителем двух элементов кольца целостностиназывается такой элемент, обозначаемый символоми обладающий двумя свойствами:

1. ;

2. .

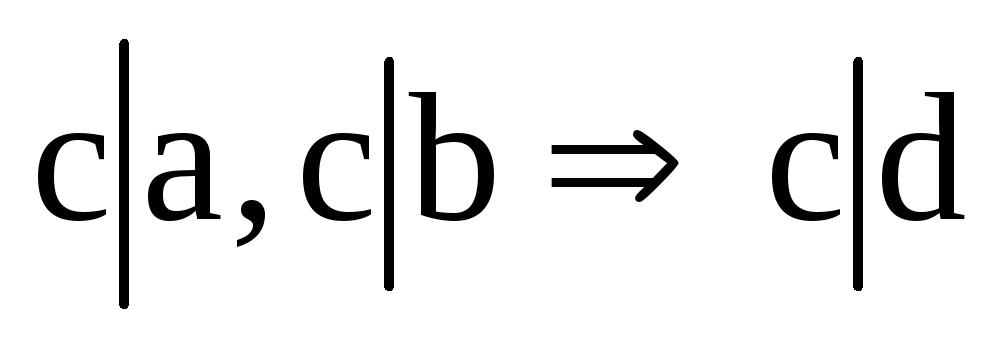Замечание. Ясно, что вместе с свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если– НОД элементов, то формально это записывается в видеили. Если также и, то элементыиделятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если, то, очевидно,, где– любой делитель единицы. Таким образом НОД элементовопределяется с точностью до сомножителя, который является делителем единицы.

С учетом этого замечания к свойствам 1., 2. Наибольшего общего делителя добавляются следующие:

3. ;

4. ;

5. ;

6. .

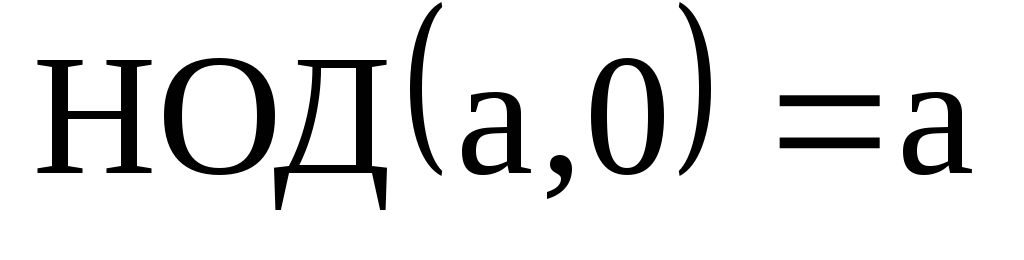Свойство 6. позволяет распространить понятие НОД на произвольное конечное число элементов кольца целостности .

По аналогии с вводится дуальное понятиенаименьшего общего кратного элементовкольца целостностиопределенного с точностью до ассоциированности и обладающее также двумя свойствами:

;

.

В частности, полагая , получаем, что.

Теорема. Если для элементов кольца целостностисуществуюти. Тогда

а) ;

б) ,.

Доказательство. Утверждение а) вытекает непосредственно из определения . Для доказательства б) необходимо убедиться, что элемент, определенный равенством, обладает свойствами 1., 2. НОД. Действительно, из, следовательно, откуда после сокращения на, допустимого в любом кольце целостности, имеем, т.е.. Аналогично, т.е.. Этим доказано свойство 1. Для доказательства свойства 2. Представим. Положим. Тогда– общее кратное элементови. Согласно свойствудля некоторого, откуда, т.е.и, что и требовалось доказать.

Определение. Элементы кольца целостностиназываются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД.

Пусть – произвольный делитель единицы, и– произвольный элемент кольца целостности. Тогда из условияследует, что. Это означает, что все элементы ассоциированные с элементом, и все делители единицы являются делителями элемента. Их называюттривиальными или несобственными делителями элемента . Все делители отличные оти, если такие существуют в, называютсянетривиальными, или собственными делителями элемента .

Пример. В кольце целых чисел тривиальными делителями числа 10 являются числаи, а нетривиальными – числаи.

Определение. Элемент кольца целостностиназывается неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элементназывается разложимым, или составным, если он имеет нетривиальные делители.

Другими словами, элемент называется разложимым, если его можно представить в виде произведениядвух нетривиальных делителей; элемент– называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.

Пример. В кольце целых чисел неразложимыми являются числат.е. простые числа и противоположные простым. Все остальные числа отличные от, – разложимы.

Неразложимые элементы обладают следующими свойствами:

• если элемент кольца целостностинеразложимый, то и любой ассоциированный с ним элементтакже неразложимый;

• если – произвольный элемент кольца целостности, а– неразложимый элемент из, то илиделится на, илии– взаимно простые элементы из.

Действительно, первое свойство следует непосредственно из свойства 7 делимости элементов кольца целостности. Второе свойство докажем следующим образом. Если НОД, токак делитель неразложимого элемента, является либо некоторым делителем единицы, либо элементом вида. В первом случае элементыивзаимно простые, во втором –делится на.

Определение. Кольцо целостности называется кольцом с однозначным разложением на простые множители ( или факториальным кольцом), если любой элементизможно представить в виде:

, (46)

где обратный элемент, а– простые элементы (не обязательно попарно различные), причем из существования другого такого разложения

следует, что и при надлежащей нумерации элементовибудет

,,…,,

где – обратные элементы в. Допуская в разложении (46), мы принимаем соглашение, что обратимые элементыв кольце целостноститакже имеют разложение на простые множители. Ясно, что если– простой, аобратный элемент в, то ассоциированный сэлементтоже простой.

Пример. В кольце целых чисел 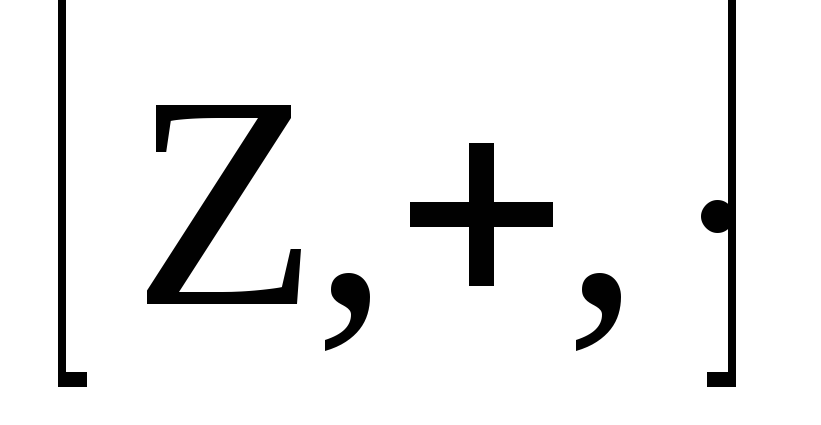с обратимыми элементамииотношение порядкадает возможность выделитьположительное простое число из двух возможных простых элементов.

Теорема. Пусть – произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в(факториальность) имеет место тогда и только тогда, когда любой простой элемент, делящий произведение, делит по крайней мере один из сомножителейили.

Доказательство. Пусть . Если

разложения на простые множители, а– кольцо с однозначным разложением, то из равенствследует, что элементассоциирован с одним изили, т.е.делитили.

Обратно, установим однозначность разложения в , гдеили. Рассуждая по индукции, допустим, что разложение всех элементов изс числомпростых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).

Докажем теперь это для любого элемента , который может быть разложен напростых сомножителей. Именно, пусть

(47)

– два разложения элемента с.

Условие теоремы, примененное к дает нам, чтодолжен делить один из элементов. Без ограничения общности (это вопрос нумерации) будем считать, что. Но– простой элемент, поэтому, где – обратимый элемент. Используя закон сокращения в , получаем из (41) равенство

. (48)

В левой части равенства (42) стоит произведение простых сомножителей. По предположению индукциии оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.

Замечание. В произвольном кольце целостности элементвообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.

Пример. Рассмотрим кольцо целостности , где.

Норма каждого отличного от нуля элемента– целое положительное число. Если элементобратим в, то, откуда. Это возможно лишь при . Таким образом в , как и в 1, обратимыми элементами являются только. Если, то. Так как, то при заданномчисло множителейне может неограниченно расти. Следовательно, разложение на простые множители ввозможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:

.

Неассоциированность элементов 3 и очевидна. Далее,. Поэтому из разложениядляилис необратимымиследовало бы, т.е., что невозможно, поскольку уравнениеснеразрешимо. Этим доказана простота элементов 3 и.