2. Гомоморфные отображения.

С точки зрения алгебры изоморфные группы неразличимы, так как не существует способа отличить одну изоморфную группу от другой.

Однако такое отождествление в некоторых случаях становится «несколько преувеличенным», «жестким» требованием.

Рассмотрим две группы G и . Пусть

некоторое отображение. Выясним, удовлетворяет ли оно всем условиям, предъявляемым к изоморфизму. Эти условия сводятся к следующему:

1. Каждый элемент группы G имеет образ в группе (образы различных элементов различны, т.е. – инъективное отображение).

2. Каждый элемент группы имеет прообраз в G (т.е. – отображение на все множество, т.е.  – сюрьективно).

3. Групповая операция при отображении  сохраняется.

Таким образом, принципиальным отличием  от простого отображения множеств является третье условие.

Если , то,

где .

Если потребовать выполнение только этого условия, то получим важный тип отображений, называемых гомоморфизмами (греч. homos – одинаковый, равный морфизм).

Определение. Отображение группыв группуназываетсягомоморфизмом, если

,

где .

Другими словами, гомоморфизмом называется отображение (не обязательно биективное) одной группы в другую, сохраняющее групповую операцию.

Если гомоморфизм удовлетворяет какому-либо из условий (1), (2), то мы получаем разновидности гомоморфизмов, имеющие специальные названия.

Определение. Гомоморфизм, являющийся инъективным отображением, называется мономорфизмом.

Определение. Гомоморфизм, являющийся сюрьективным отображением, называется эпиморфизмом.

Определение. Если гомоморфизм, является биективным отображением, то он называется изоморфизмом.

Общий вывод. Существует один тип отображений группы G в , сохраняющий групповую операцию – гомоморфизм и три его менее общие разновидности (рис. 3).

Рис. 3 – Гомоморфизм групп и его разновидности

Пусть  – произвольный гомоморфизм группы G в . Рассмотрим все элементы группы, которые можно представить в виде.

В этом случае множество элементов представляет собой область значений функции.

Определение. Образом гомоморфизма  называется множество

Можно показать, что является подгруппой в, т.е. сохраняет не только групповую операцию, но и содержит единичный и обратные элементы.

3 Ядро гомоморфизма

Рассмотрим элементы группы G, которые гомоморфизм  отображает в единичный элемент группы(рис. 4).

Определение. Ядром гомоморфизма называется множество

Рис. 4 – Ядро гомоморфизма

Лемма. Ядро гомоморфизма является подгруппой в G.

Доказательство. Для доказательства леммы просто проверим выполнение всех аксиом группы:

1. Замкнутость .

Пусть . Это означает, что

.

2. Наличие единичного элемента , т.е..

3. Наличие обратного элемента, принадлежащего .

Пусть ,

тогда .

Замечание. 1. В определении ядра гомоморфизма от отображения  не требуется никаких дополнительных условий, т.е. не только биективности, но и не инъективности, не сюрьиктивности.

2. Главное отличие гомоморфизма от изоморфизма заключается в наличии нетривиального ядра , т.е. если, то – гомоморфизм, если , т.е., то – изоморфизм.

Пример. Ядро линейного оператора. Пусть и– арифметические линейные пространства векторов размерности n и m.

Определение. Множество элементов векторов столбцовили строкназывается линейным пространством, если в нем определены две операции:

• cложение .

• умножение на скаляр .

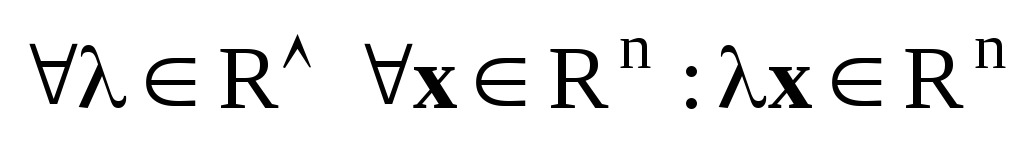Кроме того, для любых выполняются следующие аксиомы:

• ассоциативность операции сложения ;

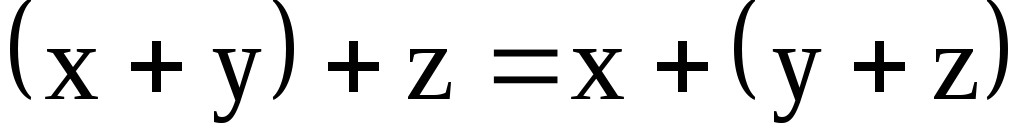• коммутативность операции сложения ;

• существование единичного или нейтрального элемента

• существование обратного (противоположного) элемента .

Таким образом, в линейном пространстве выполняются аксиомы группы, следовательно- это аддитивная абелева группа векторов столбцов размерности n.

Рассмотрим две абелевы группы ии отображение

.

Отображение А представляет собой матрицу размерности m на n, т.е.

Определение. Отображение называетсялинейным оператором, если выполняются следующие условия:

где .

Таким образом, линейный оператор есть гомоморфизм аддитивных групп линейных векторных пространств в.

Определение. Ядром линейного оператора называется множество

.

Таким образом, ядро линейного оператора – это множество решений однородной системы линейных алгебраических уравнений с матрицей A.

Утверждение. Ядром линейного оператора есть подпространство в, называемое пространством решений однородной системы линейных уравнений:

.

Доказательство. Для доказательства утверждения проверим выполнение аксиом группы для :

1. Замкнутость множества относительно операции сложения.

Пусть , тогда необходимо найти суммуи показать, что она также принадлежит ядру:

.

2. Существование обратного элемента:

.

Другими словами, необходимо показать, что . Действительно,

.

Следовательно .

3. Пусть , тогда мы должны доказать, что.

Действительно, , т.е..

Вывод. Значение абстрактной алгебры (и математики в целом) состоит не только в том, что она позволяет кратко записывать громоздкие объекты, но и в том, что она позволяет экономно мыслить, исследуя вместо многих конкретных примеров – их общие закономерности.