Лекция 7 Морфизмы групп

Для исследования общих свойств групп необходимо научиться сравнивать группы независимо от их элементов и групповых операций.

Это необходимо для ответа на вопрос: различны ли эти группы или одинаковы?

Такое исследование мы начнем со сравнения двух групп, не раскрывая смысл групповой операции и природы элементов группы.

Пусть G и – две группы с операциями и * соответственно. Как их сравнить? Наиболее простой прием, если группы конечны, построить для них таблицы Кэли.

Пусть , а элементы группы имеют вид:

, .

Таблица Кэли для группы G Таблица Кэли для группы

Таблица Кэли содержит полную информацию о группе. Анализ таблицы Кэли позволит установить многие свойства группы, например:

• в каждой строке и в каждом столбце элемент группы G встречается только один раз;

• группа G абелева тогда и только тогда, когда таблица Кэли симметрична, т.е. .

Однако сравнивать две таблицы Кэли для групп G и одинакового порядка довольно затруднительно, т.к. вид таблицы Кэли зависит от нумерации элементов группы. Для бесконечных групп ситуация еще более осложняется.

Наиболее эффективный подход к сравнению (отождествлению или различию) групп идает понятиеизоморфизма (isos – греч. –равный, одинаковый, подобный; morphe – греч. – форма) (сходный по форме).

Определение. Две группы G и с операциями и  называются изоморфными, если существует отображение

такое, что:

• (отображение  сохраняет групповую операцию);

•  – биективно.

Если

.

Тогда

, ,,,(рис. 1).

Рис. 1 – Изоморфизм групп и.

Изоморфизм групп иобозначается.

1. Простейшие свойства изоморфизмов

1. Единица группы G переходит в единицу группы .

Доказательство. Если , то

:

и, следовательно, если : – изоморфизм, то

.

2. – отображение обратного элемента совпадает с элементом, обратным(рис. 2).

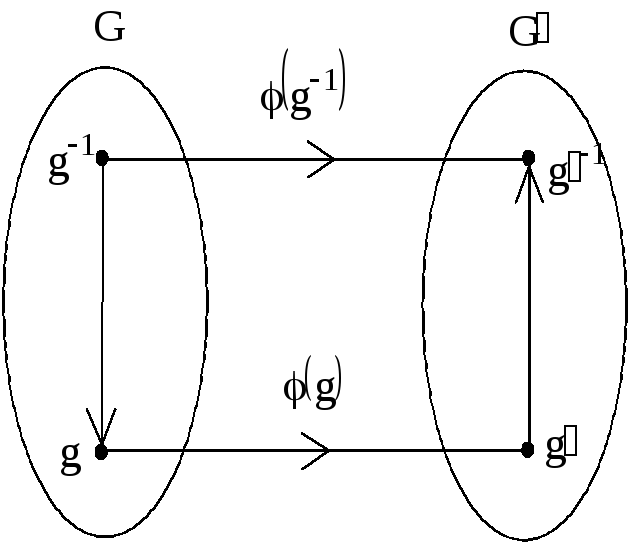
Рис. 2 – Отображение обратного элемента

Доказательство. Пусть , тогда

,

где – единицы группы.

С другой стороны, , тога

.

3. Отображение обратное к изоморфизму также является изоморфизмом.

Доказательство. Пусть

,

тогда ввиду биективности существуют

и .

Так как – изоморфизм, то

,

отсюда, переходя к обратному отображению, имеем:

,

но

, .

Замечание. 

1. С точки зрения алгебры, изоморфные группы неразличимы: отображение, порождающее изоморфизм, подобно зеркалу, переводит элементы и групповую операцию одной группы в элементы и групповую операцию другой группы.

2. Множество групп, изоморфных данной, принято понимать как абстрактную группу. Эта абстрактная группа называется представителем любой из изоморфных групп.

Пример. Пусть G – мультипликативная группа положительных вещественных чисел, т.е.

,

а – аддитивная группа всех вещественных чисел, т.е.

.

Изоморфное отображение имеет вид:

.

Известное свойство логарифма

моделирует свойство сохранения групповой операции в определении изоморфизма групп

.

Обратным к  служит отображение

такое, что

.

Докажем две общие теоремы, иллюстрирующие роль изоморфизма в теории групп.

Теорема. Все циклические группы одного и того же порядка (в том числе и бесконечного) изоморфны.

Доказательство. Пусть G – бесконечная циклическая группа, это означает, что

причем все степени различны.

В качестве группы рассмотрим бесконечную аддитивную группу целых чисел, т.е.

.

Это позволяет построить изоморфизм вида:

или ,

полагая

. (1)

Биективность (1) очевидна, а свойство

следует из теоремы о степенях элементов группы. Тогда

.

2. Пусть теперь G и – конечные циклические группы порядка q, т.е.

, .

Операции в G и не различаем. Определим биективное отображение

такое, что

, .

Полагая

, ,

имеем

.

Теорема Кэли. Любая конечная группа порядка n изоморфна некоторой подгруппе симметрической группы .

Доказательство. Пусть G – некоторая конечная группа порядка n, т.е.

.

-элементы группы G.

Так как все элементы группы G различны, то на множестве этих элементов можно построить группу всех биективных отображений множества G на себя (природа элементов группы G для нас несущественна).

Для любого элемента рассмотрим отображение

,

определяемое выражением

, .

Если – все элементы группы G, то если

будут те же элементы группы G, но расположенные в некотором другом порядке.

Действительно, если

.

Следовательно, – биективное отображение (перестановка), для которого выполняются два условия:

–сюрьективное отображение (каждый из элементов имеет прообраз);

–инъективно, т.к. образы различных элементов различны.

Следовательно, – биективное отображение, обратным к которому будет

.

Единичным отображением будет, естественно, отображение где

.

Используя ассоциативность умножения в G, получаем

,

т.е. .

Таким образом, множество биективных отображений

,

содержит единичное отображение, обратное, замкнуто относительно композиции отображений и, следовательно, образует подгруппу H в группе всех биективных отображений множества G на себя, т.е. в .

Таким образом, мы имеем включение и отображение, обладающее по вышесказанному всеми свойствами изоморфизма.

Замечание. 1. Теорема Кэли, несмотря на свою простоту, имеет важное значение в теории групп.

Она выделяет некоторый универсальный объект

(семейство симметрических групп

, ),

являющийся вместилищем всех конечных групп, рассматриваемых с точностью до изоморфизма.

Фраза "с точностью до изоморфизма" отражает сущность не только теории групп, стремящейся объединить в один класс все изоморфные группы, но и математики в целом, которая без таких обобщений была бы лишена смысла.

Определение. Положив в определении изоморфизма, мы получим изоморфное отображениегруппы G на себя. Такое отображение называетсяавтоморфизмом группы G.

Пример. Единичное отображение

вида

– автоморфизм, но G обладает и нетривиальными автоморфизмами.

Пусть аддитивная группа целых чисел.

Рассмотрим отображение , такое, что

,

т.е. отображение  изменяет знак целого числа на противоположный.

Отображение  – изоморфизм аддитивной группы целых чисел самой себе, т.е. автоморфизм.

Тем не менее, элементы этой группы не совпадают со своими образами при отображении .

Если бы они совпадали, то выполнялось бы равенство

, ,

что, очевидно, невозможно при .