Морфизмы групп

Определение. Две группы G и с операциями и  называются изоморфными, если существует отображение

такое, что:

• (отображение  сохраняет групповую операцию);

•  – биективно.

. Простейшие свойства изоморфизмов

1. Единица группы G переходит в единицу группы .

2. – отображение обратного элемента совпадает с элементом, обратным(рис. 2).

Рис. 2 – Отображение обратного элемента

3. Отображение обратное к изоморфизму также является изоморфизмом.

Теорема. Все циклические группы одного и того же порядка (в том числе и бесконечного) изоморфны.

Теорема Кэли. Любая конечная группа порядка n изоморфна некоторой подгруппе симметрической группы .

Гомоморфные отображения.

Определение. Отображение группыв группуназываетсягомоморфизмом, если

,

где .

Другими словами, гомоморфизмом называется отображение (не обязательно биективное) одной группы в другую, сохраняющее групповую операцию.

Если гомоморфизм удовлетворяет какому-либо из условий (1), (2), то мы получаем разновидности гомоморфизмов, имеющие специальные названия.

Определение. Гомоморфизм, являющийся инъективным отображением, называется мономорфизмом.

Определение. Гомоморфизм, являющийся сюрьективным отображением, называется эпиморфизмом.

Определение. Если гомоморфизм, является биективным отображением, то он называется изоморфизмом.

Определение. Образом гомоморфизма  называется множество

Можно показать, что является подгруппой в, т.е. сохраняет не только групповую операцию, но и содержит единичный и обратные элементы.

3 Ядро гомоморфизма

Рассмотрим элементы группы G, которые гомоморфизм  отображает в единичный элемент группы(рис. 4).

Определение. Ядром гомоморфизма называется множество

Рис. 4 – Ядро гомоморфизма

Лемма. Ядро гомоморфизма является подгруппой в G.

. Ядро линейного оператора. Пусть и– арифметические линейные пространства векторов размерности n и m.

Определение. Множество элементов векторов столбцовили строкназывается линейным пространством, если в нем определены две операции:

• cложение .

• умножение на скаляр .

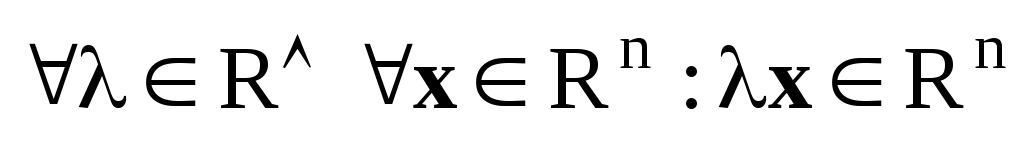Кроме того, для любых выполняются следующие аксиомы:

• ассоциативность операции сложения ;

• коммутативность операции сложения ;

• существование единичного или нейтрального элемента

• существование обратного (противоположного) элемента .

Таким образом, в линейном пространстве выполняются аксиомы группы, следовательно- это аддитивная абелева группа векторов столбцов размерности n.

Рассмотрим две абелевы группы ии отображение

.

Отображение А представляет собой матрицу размерности m на n, т.е.

Определение. Отображение называетсялинейным оператором, если выполняются следующие условия:

где .

Таким образом, линейный оператор есть гомоморфизм аддитивных групп линейных векторных пространств в.

Определение. Ядром линейного оператора называется множество

.

Таким образом, ядро линейного оператора – это множество решений однородной системы линейных алгебраических уравнений с матрицей A.

Утверждение. Ядром линейного оператора есть подпространство в, называемое пространством решений однородной системы линейных уравнений:

.