Циклические группы конечного порядка

В качестве примера циклической группы конечного порядка рассмотрим группу вращений правильного n-угольника относительно его центра .

Элементами группы

являются повороты n-угольника против часовой стрелки на углы

:

Элементами группы являются

При этом

,

а из геометрических соображений ясно, что

и

.

Группа содержитn элементов, т.е. , а образующим элементом группыявляется, т.е.

.

Пусть , тогда (см. рис. 1)

.

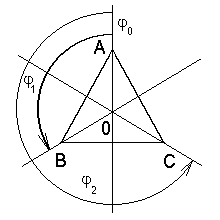
Рис. 1 – Группа – вращений правильного треугольника АВС относительно центра О.

Таблица Кэли

Анализ конечных групп наиболее наглядно осуществлять с помощью таблицы Кэли, которая является обобщением известной «таблицы умножения».

Пусть группа G содержит n элементов.

В этом случае таблица Кэли представляет собой квадратную матрицу имеющую n строк и n столбцов.

Каждой строке и каждому столбцу соответствует один и только один элемент группы.

Элемент таблицы Кэли, стоящий на пересечении i-той строки и j-того столбца, равен результату выполнения операции «умножения» i-го элемента с j-тым элементом группы.

Пример. Пусть группа G содержит три элемента{g₁,g₂,g₃}.Операция в группе «умножение».В этом случае таблица Кэли имеет вид:

Для треугольника, а группа содержит шесть элементов

,

где это повороты (см. рис. 2) вокруг высоты, медианы, биссектрисы имеют вид:

;

,

, .

Рис. 2. – Группа – преобразований симметрии правильного треугольника АВС.

Симметрическая группа

Пусть X – конечное множество из n элементов, т.е. . Поскольку мы договорились не говорить, что из себя представляют элементы множества X, то пусть.

Рассмотрим биективное отображение множества X в X. Обозначим– множество всех биективных отображений X в X.

Покажем, что – группа. Она называется симметрической группой или группой перестановок.

Определение. Биективное отображение  конечного множества Х в Х называется перестановкой (подстановкой).

Обычно перестановка  изображается в виде следующей таблицы

, (2.25)

состоящей из области определения перестановки (прообразов) – верхняя строка, и области значений (образов)перестановки – нижняя строка, или

, (2.26)

где – переставленные соответствующим образом символы. Еслиn – фиксировано, то часто в записи перестановки используется только последняя строка, которая однозначно определяет перестановку.

Пример. Для обозначения перестановок используются символы ,,,... . Пусть , тогда перестановкупредставим в виде:

.

Операции на перестановках.

На множестве всех перестановок можно задать операцию, называемую умножением такую, что. Эту операцию определим в соответствии с общим правилом композиции отображений:

Определение. Перестановка называется обратной к перестановке, если .

Определим алгоритм получения обратной перестановки.

.

Порядок группы S_n. 

Разложение перестановок, циклы, транспозиции

Определение. Длиной цикла называется количество входящих в него элементов

Теорема. Каждая перестановка может быть представлена в виде произведениянезависимых циклов длины. Это разложение определено однозначно с точностью до порядка следования циклов.

.

Теорема 2. Порядок перестановки (порядок циклической подгруппы)равен наименьшему общему кратному (НОК) длин независимых циклов, входящих в разложение .

Теорема. Пусть  – перестановка из , а

.

какое-либо разложение  в произведении транспозиций. Тогда число

называется четностью (сигнатурой или знаком) перестановки  и полностью определяется , т.е. не зависит от способа разложения перестановки  в произведение траспозиций. Кроме того, если , то

.

Определение. Перестановка называется четной, если , и нечетной, если .

Следствие 2. Пусть перестановка разложена в произведение независимых циклов длин , где,, …,, …,– днины независимых циклов.

Тогда

.