2.9.4 Фактор-группа

Значение нормального делителя в теории групп основано на том, что из смежных классов по нормальному делителю может быть построена новая группа. Для построения такой группы определим операцию умножения на множестве смежных классов. Пусть , тогда

(2.64)

Действительно, для

Пусть H – нормальный делитель группы G. В этом случае произведение двух смежных классов G по H будет смежным классом по H. Действительно, имеем:

(2.65)

Таким образом, в множестве всех смежных классов по нормальному делителю определена операция умножения. Это означает, что фактор-множество

. (2.66)

является замкнутым относительно операции умножения смежных классов, а операция умножения смежных классов является алгебраической. Равенство (2.65) показывает, что для нахождения произведения двух данных смежных классов группы G по нормальному делителю H надо в каждом из этих классов выбрать по одному представителю и потом взять тот смежный класс, к которому принадлежит произведение выбранных представителей.

В случае если – абелева группа бинарная операция на фактор-множествевводится соотношением. Фактор-группучасто называют группойпо модулю.

Теорема. Фактор-множество смежных классов группыG по нормальному делителю H с определенной в нем операцией умножения является группой. Эта группа называется фактор-группой группы G по нормальному делителю H и обозначается символом .

Доказательство. Для доказательства покажем, что в 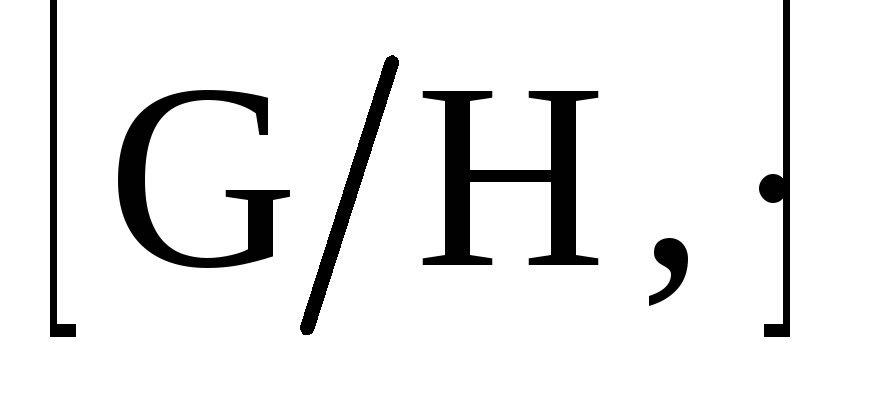будут выполнены все аксиомы группы:

• ассоциативность умножения смежных классов следует из ассоциативности умножения подмножеств группы;

• роль единицы играет сама подгруппа – нормальный делитель:

• для смежного класса обратным является классдействительно:

Выводы. Со всякой группой G связан целый набор новых групп – ее фактор-групп [G/H, ] по различным нормальным делителям.

Примеры. 1. Пусть – аддитивная группа целых чисел , а– подгруппа целых чисел, делящихся наm без остатка. Подгруппа – нормальный делитель так как– подгруппа аддитивной группы.

Фактор-группа состоит из смежных классов– классов вычетов по модулю:

Класс вычетов

Пусть , тогда таблица Кэли для фактор-группыимеет вид:

+	[0]5	[1]5	[2]5	[3]5	[4]5
[0]5	[0]5	[1]5	[2]5	[3]5	[4]5
[1]5	[1]5	[2]5	[3]5	[4]5	[0]5
[2]5	[2]5	[3]5	[4]5	[0]5	[1]5
[3]5	[3]5	[4]5	[0]5	[1]5	[2]5
[4]5	[4]5	[0]5	[1]5	[2]5	[4]5

Выводы: 1. Фактор-группа коммутативна – таблица Кэли симметрична относительно главной диагонали.

2. Фактор-группа циклическая группа. Система образующих состоит из одного элемента – смежного класса, а все остальные смежные классы совпадают с его степенями.

2. Пусть – мультипликативная группа невырожденных матриц-го порядка с вещественными коэффициентами, а– нормальный делитель этой группы, который состоит из матриц, детерминант каждой из которых равен единице. Фактор-группасостоит из смежных классов, каждый из которых содержит все матрицы, детерминант которых равен данному числу.