Лекция 8

Ядро линейного оператора.

Пусть и– арифметические линейные пространства векторов размерности n и m.

Определение. Множество элементов векторов столбцовили строкназывается линейным пространством, если в нем определены две операции:

• cложение .

• умножение на скаляр .

Кроме того, для любых выполняются следующие аксиомы:

• ассоциативность операции сложения ;

• коммутативность операции сложения ;

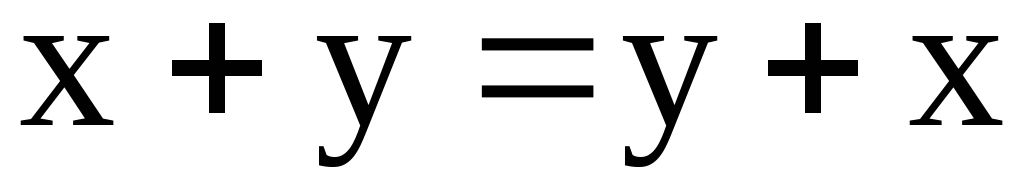• существование единичного или нейтрального элемента

• существование обратного (противоположного) элемента .

Таким образом, в линейном пространстве выполняются аксиомы группы, следовательно- это аддитивная абелева группа векторов столбцов размерности n.

Рассмотрим две абелевы группы ии отображение

.

Отображение А представляет собой матрицу размерности m на n, т.е.

Определение. Отображение называетсялинейным оператором, если выполняются следующие условия:

где .

Таким образом, линейный оператор есть гомоморфизм аддитивных групп линейных векторных пространств в.

Определение. Ядром линейного оператора называется множество

.

Таким образом, ядро линейного оператора – это множество решений однородной системы линейных алгебраических уравнений с матрицей A.

Утверждение. Ядром линейного оператора есть подпространство в, называемое пространством решений однородной системы линейных уравнений:

.

Доказательство. Для доказательства утверждения проверим выполнение аксиом группы для :

1. Замкнутость множества относительно операции сложения.

Пусть , тогда необходимо найти суммуи показать, что она также принадлежит ядру:

.

2. Существование обратного элемента:

.

Другими словами, необходимо показать, что . Действительно,

.

Следовательно .

3. Пусть , тогда мы должны доказать, что.

Действительно, , т.е..

Вывод. Значение абстрактной алгебры (и математики в целом) состоит не только в том, что она позволяет кратко записывать громоздкие объекты, но и в том, что она позволяет экономно мыслить, исследуя вместо многих конкретных примеров – их общие закономерности.

2. Смежные классы. Разложение группы по подгруппе

Пусть – произвольный гомоморфизм группыв, а– произвольный, но фиксированный элемент группы. Рассмотрим множество

Покажем, что все элементы множества отображаются в один и тот же элемент. Действительно, т.к.– гомоморфизм, то

.

Обратно, если , то его можно также представить в виде. Действительно

и .

Этот факт указывает на возможность разбиения группы на подмножества вида. Так как, то мы можем рассмотреть такое разбиение в общем случае независимо от гомоморфизмов, т.е. при произвольном выборе подгруппы H в G.

Пусть G – некоторая группа, а ее собственная подгруппа, причем.

Определение. Левым смежным классом группы G по подгруппе H называется множество элементов вида

,

где – фиксированный элемент группы(рис.5).

Определение. Правым смежным классом группы G по H подгруппе называется множество элементов вида

(рис. 6),

где – фиксированный элемент группы(рис.6).

Рис. 5 –Левый смежный класс группыпо подгруппе H.

Рис. 6 – Правый смежный класс группы G′ по подгруппе H.

Замечание. 

1. В общем случае , однако если, например,

.

2. Один из смежных классов образует сама подгруппа.

Действительно, если

,

т.е. сама подгруппа совпадает со своим смежным классом.

Утверждение.Если , то левый смежный класс не является подгруппой.

Доказательство проведем от противного. Предположим, что – подгруппа, тогда

.

Т.е. это возможно только в одном случае, когда .

Теорема.1. Два левых смежных класса группы G по подгруппе H совпадают или не имеют общих элементов.

2.Разбиение G на левые смежные классы по H определяет на G отношение эквивалентности.

Доказательство. 1. Пусть тогдаи– два левых смежных класса.

Предположим, что эти два класса имеют общий элемент

.

Покажем, что в этом случае =. Идея доказательства проста: т.к.и– множества, то необходимо показать, что

.

Действительно, если

.

С другой стороны, любой элемент классаимеет вид

,

где .

Следовательно, .

Обратное включение,

.

Любой элемент g₁h класса g₁H имеет вид

, где ,

следовательно, .

С учетом предыдущего включения окончательно имеем .

2. Покажем, что если ине имеют общих элементов, то они не совпадают.

Действительно, каждый принадлежит некоторому смежному классу, т.к.

.

Нас будет интересовать вопрос, при каких условиях будут совпадать классы

g₁H и g₂H, если .

Пусть , но.

В этом случае .

Это возможно только тогда, когда

или .

Если

, то

в том и только в том случае, если

или .

Общий вывод. 

1. Произвольный элемент g группы G принадлежит только одному смежному классу .

2. Так как принадлежит только одному классу, в котором он замещает единичный элемент, то всю группу G можно представить в виде объединения непересекающихся смежных классов, т.е.и:

,

причем

.

Такое представление было получено Галуа (1811–1832).

Полученное разбиение индуцирует на G отношение эквивалентности, которое определяется следующим образом.

(1)

Выражение (1) есть не что иное, как условие совпадения классов и,если.

Убедимся, что условие (1) определяет отношение эквивалентности на G.

Для этого необходимо показать, что для (1) выполняются:

1. рефлексивность ;

2. симметричность

;

3. транзитивность

.

Действительно

Замечание. 

1. Если G – конечная группа, например, , а

,

то любые два смежных класса группы G по H исодержат одинаковое количество элементов, а именно

.

2. Смежные классы не являются подгруппами G, за исключением самой подгруппы H, т.к. не содержат e.

Пример. Пусть G – аддитивная группа векторов на плоскости, т.е. .

В качестве подгруппы выберем ось OX, т.е., тогда для произвольного, но фиксированного элементалевый смежный класс группыпо подгруппеимеет вид:

.

Если вектор h пробегает всю ось OX, то конец вектора пробегает всю прямую параллельную оси OX и проходящую через конец вектора g (рис. 7).

Рис. 7 – Левый смежный класс аддитивной группы векторов на плоскости.

Определим класс эквивалентности

.

Вывод. Класс эквивалентности, это веер векторов, концы которых лежат на прямой параллельной оси OX.

Отождествляя векторы с их концами можно сказать, что класс эквивалентности – это прямая параллельная оси OX, а вся группа G (плоскость) разбивается на совокупность параллельных прямых.