
- •Лекция 2
- •1. Множество целых чисел с операцией умножения.
- •2. Множество рациональных чисел
- •3. Рациональные числа, отличные от нуля ,
- •10. Рациональные числа, отличные от нуля, не образуют группу по сложению.
- •Абстрактные группы и их свойства
- •1. Ассоциативность
- •2. Существование единичного элемента
- •3. Существование обратного элемента
- •Обобщенная ассоциативность
- •Степень элемента группы
- •Порядок элемента группы
- •2.5 Подгруппы группы. Минимальная подгруппа. Системы образующих
- •2.6 Циклические группы
2.5 Подгруппы группы. Минимальная подгруппа. Системы образующих
Рассмотрев
некоторые элементарные свойства групп,
перейдем к анализу взаимосвязей между
различными группами. Такой анализ мы
начнем с групп с совпадающими операциями.
Это приводит к понятию подгруппы группы.
Рассмотрим две группы
![]()
![]() ,
,![]() .
.
Определение. Группа
![]() называется подгруппой группы
называется подгруппой группы![]() ,
если
,
если
![]() и групповые операции
и
совпадают на множестве
и групповые операции
и
совпадают на множестве
![]() .
.
Утверждение. Для
того чтобы непустое подмножество
![]() группы
группы![]() было подгруппой, необходимо и достаточно
выполнения следующих условий:
было подгруппой, необходимо и достаточно
выполнения следующих условий:
если
 (единичный
элемент группы принадлежит подгруппе
(единичный
элемент группы принадлежит подгруппе );
);
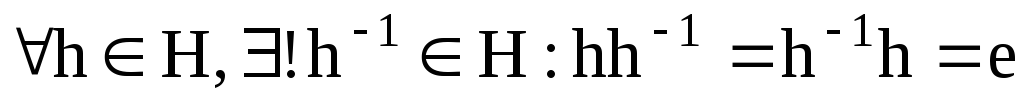 (существует
обратный элемент).
(существует
обратный элемент).
Пример 1. Пусть
![]() – аддитивная группа целых чисел. В ней
можно выделить ряд подгрупп:
– аддитивная группа целых чисел. В ней
можно выделить ряд подгрупп:
1. ![]() – подгруппу чётных чисел. Легко проверить,
что множество
– подгруппу чётных чисел. Легко проверить,
что множество![]() с заданной операцией сложения образует
группу:
с заданной операцией сложения образует
группу:
сумма двух чётных чисел – чётное число;
операция сложения чётных чисел – ассоциативна;
единичным элементом является нуль – чётное число;
число, обратное чётному числу – чётное число.
2. ![]() – подгруппу чисел кратных
– подгруппу чисел кратных![]() ;
;
3. ![]() – подгруппу, содержащую только нуль;
– подгруппу, содержащую только нуль;
4. ![]() – подгруппу целых чисел.
– подгруппу целых чисел.
Пример 2. Рассмотрим
аддитивную группу рациональных чисел
![]() .
В ней можно выделить следующие подгруппы:
.
В ней можно выделить следующие подгруппы:
подгруппу целых чисел
 ;
;
все подгруппы аддитивной группы целых чисел;
рациональные числа, представимые в виде дробей с нечётными знаменателями: если знаменатели дробей
 и
и нечётны, то и их сумма – дробь
нечётны, то и их сумма – дробь – имеет нечетный знаменатель, нуль
можно представить в виде дроби с нечётным
знаменателем
– имеет нечетный знаменатель, нуль
можно представить в виде дроби с нечётным
знаменателем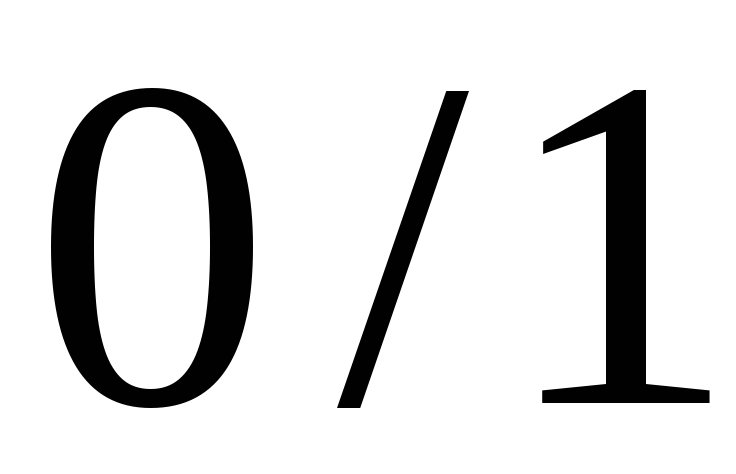 ,
а число противоположное рациональному
числу с нечётным знаменателем есть
тоже число со знаком «минус», т.е. также
может быть представлено числом с
нечётным знаменателем.
,
а число противоположное рациональному
числу с нечётным знаменателем есть
тоже число со знаком «минус», т.е. также
может быть представлено числом с
нечётным знаменателем.
Замечание. Мы
не можем утверждать, что дроби с нечётными
знаменателями образуют подгруппу,
поскольку любую такую дробь можно
представить в виде дроби с чётным
знаменателем: например, дробь
![]() можно записать в виде
можно записать в виде![]() .
Следовательно, хотя в действительности
мы имеем в виду дроби с нечётными
знаменателями, следует применять лишь
приведённое выше точное название
подгруппы.
.
Следовательно, хотя в действительности
мы имеем в виду дроби с нечётными
знаменателями, следует применять лишь
приведённое выше точное название
подгруппы.
Пример 3. Рассмотрим
мультипликативную группу вещественных
чисел, отличных от нуля
 .
В ней можно выделить следующие подгруппы:
.
В ней можно выделить следующие подгруппы:
мультипликативную группу положительных вещественных чисел
 :
произведение двух положительных
вещественных чисел положительно (и
вещественно), единица – число
положительное, число, обратное
положительному, также положительно;
:
произведение двух положительных
вещественных чисел положительно (и
вещественно), единица – число
положительное, число, обратное
положительному, также положительно;
подгруппу, состоящую из чисел
 ,
,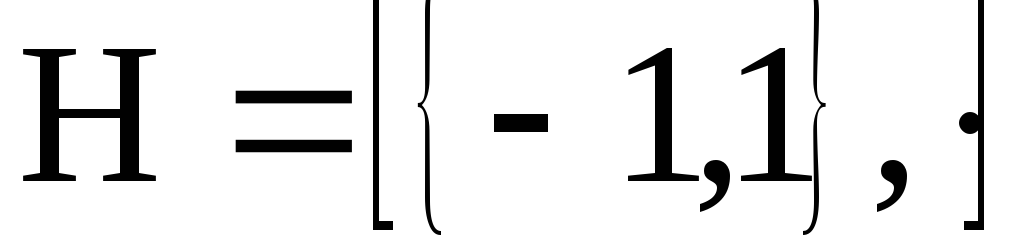 :
произведение любых двух чисел из
множества
:
произведение любых двух чисел из
множества равно либо
равно либо ,
либо
,
либо .
Каждое из двух чисел
.
Каждое из двух чисел обратно самому себе.
обратно самому себе.
Замечание. 1.
В любой группе
![]() можно выделить по крайней мере две
подгруппы:
можно выделить по крайней мере две
подгруппы:
 –подгруппу,
содержащую только один единичный
элемент.
–подгруппу,
содержащую только один единичный
элемент.
 –подгруппу,
совпадающую с самой группой.
–подгруппу,
совпадающую с самой группой.
2.
В общем случае количество выделяемых
подгрупп в группе
![]() зависит от мощности группы
зависит от мощности группы![]() .
Если
.
Если![]() и множество
и множество![]() – конечно, то конечно и количество
выделяемых подгрупп. Если
– конечно, то конечно и количество
выделяемых подгрупп. Если![]() – бесконечно, то количество выделяемых
подгрупп может быть как конечно, так и
бесконечно.
– бесконечно, то количество выделяемых
подгрупп может быть как конечно, так и
бесконечно.
Определение. Подгруппа
![]() называется собственной подгруппой,
если:
называется собственной подгруппой,
если:![]() и
и![]() .
.
В
противном случае подгруппа
![]() называется несобственной илитривиальной.
Итак,
называется несобственной илитривиальной.
Итак,
![]() – тривиальные подгруппы любой группы
– тривиальные подгруппы любой группы![]() .
.
Минимальная подгруппа. Пусть
![]() произвольное подмножество множества
произвольное подмножество множества![]() группы
группы![]() ,
попробуем выбрать подгруппу
,
попробуем выбрать подгруппу![]() группы
группы![]() ,
содержащую
,
содержащую![]() и такую, что для всякой подгруппы
и такую, что для всякой подгруппы![]() из того, что
из того, что![]() будет вытекать включение
будет вытекать включение![]() ,
т.е.
,
т.е.![]() – минимальная подгруппа, содержащая
множество
– минимальная подгруппа, содержащая
множество![]() .
.
Лемма. Двух
минимальных подгрупп
![]() и
и![]() ,
содержащих
,
содержащих![]() ,
не существует.
,
не существует.
Доказательство. Действительно,
если
![]() и
и![]() ,
где
,
где![]() ,
,![]() – две минимальные подгруппы, то из того,
что
– две минимальные подгруппы, то из того,
что![]() ,
а из того, что
,
а из того, что![]() ,
откуда следует, что
,
откуда следует, что![]() .
.
Системы образующих. Пусть
![]() – некоторая группа, и существует
семейство подгрупп {
– некоторая группа, и существует
семейство подгрупп {![]() ,
,![]() }
группы G, т.е.
}
группы G, т.е.![]() .
.
Теорема. Пересечение
![]() любого семейства подгрупп
любого семейства подгрупп![]() группы G является подгруппой.
группы G является подгруппой.
Доказательство. Пусть e – единичный элемент группы G, тогда свойства:
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
характеризующие
всякую подгруппу, выполнены в
![]() ,
т.к. они выполнены в каждой из подгрупп
,
т.к. они выполнены в каждой из подгрупп![]() в отдельности. Это свойство групп
позволяет находить в любой группе
"наименьшую" или "минимальную"
подгруппу, содержащую заданное множество
в отдельности. Это свойство групп
позволяет находить в любой группе
"наименьшую" или "минимальную"
подгруппу, содержащую заданное множество![]() элементов группы G. Рассмотрим множество
элементов группы G. Рассмотрим множество![]() элементов группы G. Наименьшая подгруппа,
которой принадлежат эти элементы,
содержится во всякой другой подгруппе,
включающей в себя помимо элементов
множества S, еще какие-то другие элементы
группы
элементов группы G. Наименьшая подгруппа,
которой принадлежат эти элементы,
содержится во всякой другой подгруппе,
включающей в себя помимо элементов
множества S, еще какие-то другие элементы
группы![]() .
.
Выберем
теперь в качестве семейства
![]() все те подгруппы, которые содержат
данное множество S, тогда их пересечение
все те подгруппы, которые содержат
данное множество S, тогда их пересечение
![]() (2.20)
(2.20)
и будет минимальной "наименьшей" подгруппой, содержащей множество S.
Определение. Подгруппа
![]() ,
определяемая в виде (2.20), называется
минимальной подгруппой, содержащей
множество S.
,
определяемая в виде (2.20), называется
минимальной подгруппой, содержащей
множество S.
Замечание. На
первый взгляд минимальная подгруппа
![]() задается неконструктивно, поскольку
необходимо перебирать все подгруппы
задается неконструктивно, поскольку
необходимо перебирать все подгруппы![]() ,
содержащие заданное множество S, а затем
найти их пересечение. Необходимости в
этом, однако, нет. Покажем это.
,
содержащие заданное множество S, а затем
найти их пересечение. Необходимости в
этом, однако, нет. Покажем это.
Пусть
![]() .
Поскольку подгруппа
.
Поскольку подгруппа![]() содержит элементы a, b, c, то три элемента
этой подгруппы уже известны. Кроме того,
мы знаем, что подгруппе
содержит элементы a, b, c, то три элемента
этой подгруппы уже известны. Кроме того,
мы знаем, что подгруппе![]() принадлежит единичный элемент e. Из
обобщенной ассоциативности следует,
что вместе с каждым из элементов a, b, c
подгруппе
принадлежит единичный элемент e. Из
обобщенной ассоциативности следует,
что вместе с каждым из элементов a, b, c
подгруппе![]() принадлежат и все (целые) степени ее
элементов, а так же все произведения
степеней. Следовательно, подгруппа
принадлежат и все (целые) степени ее
элементов, а так же все произведения
степеней. Следовательно, подгруппа![]() состоит из элементов вида:
состоит из элементов вида:
![]() , (2.21)
, (2.21)
где
![]() – целые числа.
– целые числа.
Замечание. 1. Некоторые из произведений вида (2.21) могут не содержать какого либо из элементов {a, b, c}, но их также можно представить в виде (2.21), положив соответствующие показатели степени равными нулю.
2. Единичный элемент e также можно представить в виде (2.21), положив все показатели степени равными нулю.
Вывод. Подгруппа
![]() ,
порожденная элементами множества
,
порожденная элементами множества![]() ,
состоит из произведений степеней
образующих элементов вида (2.20).
,
состоит из произведений степеней
образующих элементов вида (2.20).
Сформулируем этот вывод в виде следующего утверждения.
Утверждение. Минимальная
подгруппа
![]() группы G совпадает с множеством T,
состоящим из единичного элемента e и
всевозможных произведений:
группы G совпадает с множеством T,
состоящим из единичного элемента e и
всевозможных произведений:
![]() ,
(2.22)
,
(2.22)
где:
либо
![]() ,
либо
,
либо![]() .
.
Доказательство. Если
![]() ,
,![]() следовательно
следовательно![]() и если
и если![]()
![]() то множество T является подгруппой в G.
С другой стороны, каждая подгруппа H,
содержащая все
то множество T является подгруппой в G.
С другой стороны, каждая подгруппа H,
содержащая все
![]() ,
должна содержать все их обратные
,
должна содержать все их обратные![]() и, стало быть, все их произведения вида
и, стало быть, все их произведения вида![]() .
Поэтому
.
Поэтому![]() и T совпадает с пересечением всех этих
подгрупп.
и T совпадает с пересечением всех этих
подгрупп.
Замечание. Далеко
не все произведения
![]() будут различными элементами подгруппы
будут различными элементами подгруппы
![]() ,
даже если условиться заменять все
встречающиеся пары
,
даже если условиться заменять все
встречающиеся пары![]() ,
,![]() взаимно обратных элементов единичным
элементом. В общем случае при
взаимно обратных элементов единичным
элементом. В общем случае при![]() вопрос о равенстве произведений
вопрос о равенстве произведений
![]() достаточно сложен.
достаточно сложен.
Определение. Если
подгруппа
![]() ,
порожденная элементами множества S,
совпадает со всей группой G, то элементы
множества S называютсясистемой
образующих
элементов группы
,
порожденная элементами множества S,
совпадает со всей группой G, то элементы
множества S называютсясистемой
образующих
элементов группы
![]() .
.
Определение. Если
множество S конечно, то группа
![]() ,
порожденная множеством S, называется
конечнопорожденной группой.
,
порожденная множеством S, называется
конечнопорожденной группой.
Утверждение. Каждая группа G порождается какой-нибудь системой образующих S.
Доказательство. Пусть
G – группа, порождённая конечным
множеством S своих элементов. Удаляя из
S "лишние" элементы, которые
записываются в виде произведения
оставшихся и их обратных, мы придем к
минимальной системе образующих
![]() группы G, где
группы G, где![]() .
Это означает, что
.
Это означает, что![]() ,
но
,
но![]() ,
если система образующих
,
если система образующих![]() получена из
получена из![]() удалением хотя бы одного элемента. Пусть
удалением хотя бы одного элемента. Пусть![]() .
Тогда вместо
.
Тогда вместо![]() пишут также
пишут также![]() .
.
Пример 1. Пусть
G – аддитивная группа целых чисел, т.е.
![]() .
Необходимо найти минимальную подгруппу
.
Необходимо найти минимальную подгруппу![]() группы G, порожденную множеством S, если:
группы G, порожденную множеством S, если:
1. ![]() ,
2.
,
2. ![]() ,
3.
,
3. ![]() ,
4.
,
4. ![]() ,
5.
,
5. ![]() .
.
Решение.
1. Если S={2}, то
![]() ;
;
Если S={4, 6}, то
 .
Ясно, что все элементы подгруппы
.
Ясно, что все элементы подгруппы четные т.к. общий элемент
этой подгруппы
можно представить в виде четного числа
четные т.к. общий элемент
этой подгруппы
можно представить в виде четного числа .
Естественно,
возникает вопрос, все ли четные числа
содержатся в данной подгруппе? Для
ответа на этот вопрос необходимо
проверить, принадлежит ли число два
этой подгруппе. Если число два принадлежит
подгруппе
.
Естественно,
возникает вопрос, все ли четные числа
содержатся в данной подгруппе? Для
ответа на этот вопрос необходимо
проверить, принадлежит ли число два
этой подгруппе. Если число два принадлежит
подгруппе
 ,
то и все его степени (т.е. четные числа)
принадлежат этой подгруппе.
,
то и все его степени (т.е. четные числа)
принадлежат этой подгруппе.
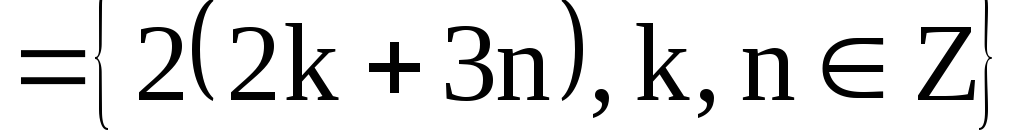 .
Пусть
.
Пусть Тогда имеем
Тогда имеем ,
следовательно,
,
следовательно, и подгруппа
и подгруппа будет содержать все элементы, порожденные
числом два, т.е. все четные числа.
будет содержать все элементы, порожденные
числом два, т.е. все четные числа.Если S={0}, тогда

Если S={1}, то

Если S={–1}, то

Пример 2. Пусть
G – мультипликативная группа положительных
вещественных чисел, т.е.
![]() .
Необходимо найти минимальную подгруппу
.
Необходимо найти минимальную подгруппу![]() группы G, порожденную множеством S, если:
1.
группы G, порожденную множеством S, если:
1.![]() ,
2.
,
2.![]() .
.
Решение. 1. Если
![]() ,
то
,
то![]()
![]() ;
;
2. Если
S={1}, то

Пример 3. Пусть
![]() – аддитивная группа рациональных чисел.
Необходимо найти минимальную подгруппу
– аддитивная группа рациональных чисел.
Необходимо найти минимальную подгруппу![]() группы G, порожденную множеством
группы G, порожденную множеством![]() .
.
Решение. В
минимальную подгруппу
 должны входить все целые кратные
рационального числа
должны входить все целые кратные
рационального числа![]() .
Кроме того, подгруппе
.
Кроме того, подгруппе принадлежит любое целое число четвертых,
восьмых и т.д. Следовательно, эта подгруппа
содержит все дроби, в знаменатель которых
не входят никакие простые числа, кроме
2 (т.е. в знаменателе могут стоять лишь
степени числа 2). Но такие дроби образуют
подгруппу, содержащую все заданные
числа. Следовательно, минимальная
подгруппа
принадлежит любое целое число четвертых,
восьмых и т.д. Следовательно, эта подгруппа
содержит все дроби, в знаменатель которых
не входят никакие простые числа, кроме
2 (т.е. в знаменателе могут стоять лишь
степени числа 2). Но такие дроби образуют
подгруппу, содержащую все заданные
числа. Следовательно, минимальная
подгруппа состоит из дробей, знаменателями которых
служит степень числа 2.
состоит из дробей, знаменателями которых
служит степень числа 2.
