1. Множество целых чисел с операцией умножения.

В множестве целых чисел умножение всегда выполнимо, т.е. произведение любых двух целых чисел также является целым числом.

Т.к. , такой, что, но. Например, для числаневозможно указать такое целое число, которое удовлетворяет соотношению.

Следовательно, целые числа не образуют группу по умножению.

Замечание. Нетрудно заметить, что послужило препятствием к образованию группы: в множестве целых чисел деление выполнимо не во всех случаях. Следовательно, следует рассматривать лишь такие множества чисел, в которых деление всегда выполнимо. «Деление» следует понимать, как .

2. Множество рациональных чисел

,

с групповой операцией умножения .

Поскольку произведение двух рациональных чисел – число рациональное, то обычное умножение не выводит за пределы множества рациональных чисел. Проверим, все ли аксиомы группы выполняются:

умножение ассоциативно;

единица - рациональное число;

проверим, существует ли обратный элемент.

Если рациональное число (дробь) умножить на обратное число, то получится 1.

Возникает вопрос: для всякого ли рационального числа имеется обратное?

Единственное исключение составляет «нуль». Причина “ущербности” нуля состоит в том, что при умножении его на любое число всегда получается нуль, но не единица. Следовательно, обратный элемент существует не для всех рациональных чисел.

Поэтому рациональные числа не образуют группу по умножению.

3. Рациональные числа, отличные от нуля , образуют группу по умножению.

4.  Множество положительных рациональных чисел с операцией умножения .

Поскольку число, обратное положительному рациональному числу, также положительно и рационально, то положительные рациональные числа образуют группу по умножению.

5. Числа ис операцией умножения.

При умножении на результат совпадает со вторым сомножителем, а. Следовательно, умножение не выводит за пределы рассматриваемого множества чисел. Проверим, выполняется ли третья аксиома (выполнение остальных аксиом очевидно). Эта аксиома выполняется, т.к. каждый из элементовисовпадает с обратным.

Следовательно, группа по умножению.

6. Отрицательные рациональные числа с операцией умножения .

Так как произведение двух отрицательных рациональных чисел – число положительное, то множество отрицательных рациональных чисел не замкнуто относительно операции умножения, и умножение не является групповой операцией. Следовательно, отрицательные рациональные числа не образуют группу по умножению.

7. Один лишь нуль , групповая операция умножение.

Так как , то умножение не выводит за пределы данного множества. В роли единичного элемента выступает нуль, т.к..

Следовательно, число 0 образует группу по умножению.

Рассмотрим теперь в качестве групповой операции операцию сложения чисел “+”.

Прежде чем рассмотреть частные случаи, установим некоторые общие свойства операции “+”;

• об ассоциативности можно не заботиться, т.к. на множестве чисел сложение всегда ассоциативно;

• единицей относительно сложения может быть такой элемент е, что для любых а выполняется условие 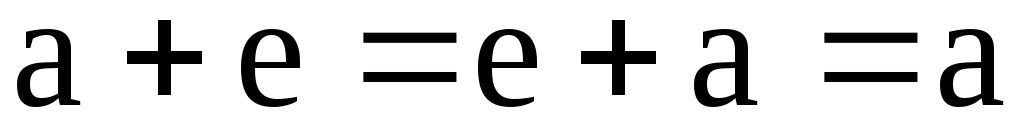. Это условие выполняется лишь для нуля.Вывод: необходимо каждый раз проверять, принадлежит ли нуль рассматриваемому множеству чисел;

• числом, ”обратным” числу , при сложении служит противоположное число, удовлетворяющее соотношению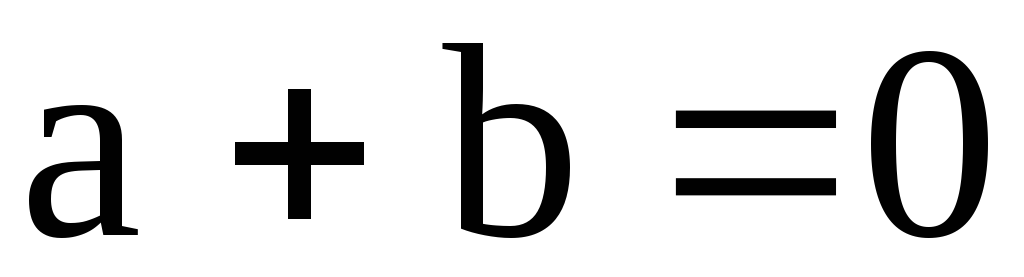. Таким числом может быть только число.Поэтому достаточно проверить, содержит ли рассматриваемое множество чисел вместе с каждым принадлежащим числом то же число, взятое со знаком “минус”.

8. Целые числа . Сумма целых чисел – целое число, следовательно операция сложения не выводит за пределы рассматриваемого множества. Так как нуль – целое число, и любое целое со знаком минус – также целое число, то целые числа образуют группу по сложению.

9. Рациональные числа образуют группу по сложению.