2.8 Морфизмы групп
Для исследования общих свойств групп необходимо научиться сравнивать группы независимо от их элементов и групповых операций. Это необходимо для ответа на вопрос: различны ли эти группы или одинаковы?
Такое исследование мы начнем со сравнения двух групп, не раскрывая смысл групповой операции и природы элементов группы.
Пусть G
и
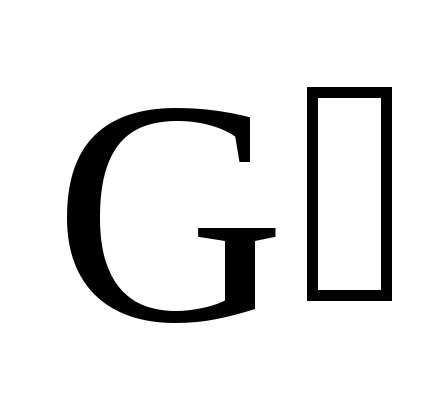– две группы с операциями
и * соответственно. Как их сравнить?
Наиболее простой прием, если группы
конечны, построить для них таблицы Кэли.
Пусть
,
а элементы группы имеют вид:
, 
.
Таблица
Кэли для группы G Таблица
Кэли для группы
Таблица Кэли содержит полную информацию о группе. Анализ таблицы Кэли позволит установить многие свойства группы, например:
в каждой строке и в каждом столбце элемент группы G встречается только один раз;
группа G абелева тогда и только тогда, когда таблица Кэли симметрична, т.е.
.
Однако сравнивать
две таблицы Кэли для групп G
и
одинакового порядка довольно
затруднительно, т.к. вид таблицы Кэли
зависит от нумерации элементов группы.
Для бесконечных групп ситуация еще
более осложняется. Наиболее эффективный
подход к сравнению (отождествлению или
различию)
групп
и
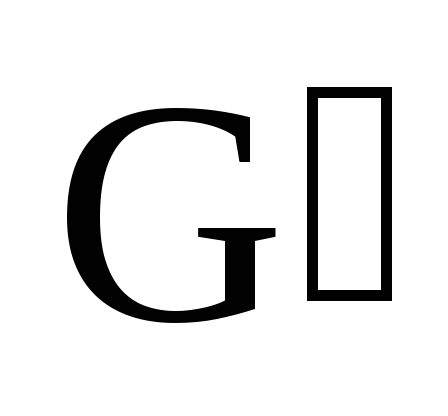дает
понятие
изоморфизма
(isos – греч. –