2.7.1 Разложение перестановок, циклы, транспозиции

Выясним, как “ведет себя” перестановка в области определения. Рассмотрим произвольную перестановку

.

Эта перестановка переводит единицу в четверку, четверку в единицу, двойка переходит в тройку, а тройка в двойку.

Если все перечисленные замены записать в той последовательности, в которой мы их производили, то рассматриваемая перестановка примет вид: . Нетрудно заметить, что перестановка оказалась, по существу, разложенной на две части. . Это означает, что наша перестановка состоит из двух независимых частей, каждая из которых перемещает элементы, принадлежащие ее собственной области определения (рис. 2.3).

Рис. 2.3 – Разложение перестановки .

Именно потому, что обе части перестановки  независимы, совершенно безразлично, какую из перестановок выполнять первой, а какую второй. Если перестановкивыполнять последовательно одну за другой, то такие действия можно рассматривать, как умножение перестановок. Однако до сих пор мы говорили об умножении перестановок в тех случаях, когда области определения перестановок совпадали. Здесь же области определения перестановок различны. Преодолеть возникшую проблему не составляет труда: условимся считать, что наши перестановки переводят каждый “недостающий” элемент в самого себя.

Таким образом, перестановка  допускает следующее разложение в произведение двух независимых перестановок:

.

Легко заметить, что в данном разложении нижние строки совершенно излишни. Действительно, верхние строки состоят из тех же элементов, что и нижние, причем каждый элемент под действием перестановки переходит в следующий. Это позволяет представить нашу перестановку в виде

.

Перестановки, стоящие в правой части, называются независимыми циклами, а представление перестановки в виде называется разложением перестановкив произведение независимых циклов.

Определение. Длиной цикла называется количество входящих в него элементов (в данном случае циклы имеют длину, равную двум). Перестановка допускает разложение только в один циклдлиной 4.

Разложение перестановки  в произведение независимых циклов эквивалентно разбиению множества  на непересекающиеся классы , где,.

Известно, что разбиение множества на непересекающиеся классы эквивалентно введению некоторого отношения эквивалентности. Элементы, входящие в один из циклов, являются эквивалентными между собой, а сами циклы представляют собой классы эквивалентности. Если некоторая перестановка определенная на множестве , которую можно представить в виде произведения независимых циклов, то элементы множества можно представить в виде объединения р попарно непересекающихся подмножеств . Таких, что.

Множества называются-орбитами. Название это вполне обоснованно. Каждая точка принадлежит в точности одному классу эквивалентности, напримерили– орбите. Если, тосостоит из образов точки i при действии степеней элемента, где– длинаk-го цикла орбиты . Очевидно, чтои, причем– наименьшее число, обладающее этим свойством. Циклможно представить в виде:

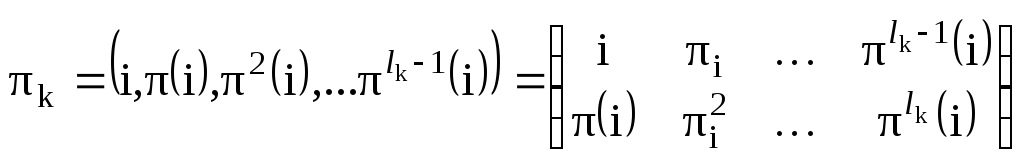.(2.28)

Цикл _k оставляет на месте все точки из множества , а для любой точки

(2.29)

Это свойство дает нам основание называть циклы независимыми или непересекающимися циклами.

Теорема. Каждая перестановка может быть представлена в виде произведениянезависимых циклов длины. Это разложение определено однозначно с точностью до порядка следования циклов.

. (2.30)

Замечание. Длина каждого k-го цикла – ,больше или равна двум. Если циклимеет длину равную единице, то он действует как единичная перестановка и его в произведении (2.29) естественно опускать.

Например, перестановку

можно представить в виде .

Запись перестановки  в виде произведения независимых циклов (2.29) позволяет легко найти порядок перестановки .

Следствие 1. Порядок перестановки (порядок циклической подгруппы) равен наименьшему общему кратному (НОК) длин независимых циклов, входящих в разложение.

Докозательство. Представим перестановку в виде произведения независимых циклов

. (2.31)

Тогда

Так как циклы независимы (они действуют на различных множествах), и еслиq – порядок циклической подгруппы, , то, где.

Следовательно? q – общее кратное порядков циклов _k, которые совпадают с их длинами . Еслиq – наименьшее положительное число, для которого ,тои

. (2.32)

Замечание. Два любых целых числа m и n можно записать в виде произведений одних и тех же простых чисел .

Например , тогда

, где

Множество простых чисел .

Пример. Определить порядок перестановки вида

.

Решение. Представим перестановку  в виде произведения независимых циклов, т.е.

.

Длины независимых цикловравны

Следовательно, порядок рассматриваемой перестановки равен 28.

Определение. Цикл длиной два называется транспозицией. Любая транспозиция имеет вид и оставляет на местах все символы за исключением.

Теорема. Каждая перестановка может быть представлена в виде произведения транспозиции.

Теорема будет доказана, если мы сможем представить в виде произведений транспозиций каждый из циклов _k, входящих в разложения перестановки: .

Рассмотрим произвольный цикл , напримери произведем его разложение в произведение транспозиций. Алгоритм разложения циклав произведение транспозиций представлен на рисунке 2.3.

Цикл транспозиции

Рис 2.3 – Разложение цикла в произведение транспозиций.

После завершения всех операций на месте каждого элемента цикла оказался следующий за ним элемент, а первый элемент перешел на последнее место. Таким образом, циклоказался разложенным в произведение транспозиций:

Естественно, это разложение не единственно. Например

.

Важно другое – и в первом и во втором его разложении имеется равное количество транспозиций – четыре. Если , то количество транспозиций равно. Раскладывая аналогичным образом каждый цикл перестановки в произведение транспозиции мы получим разложение всей перестановки в произведение транспозиций.

Замечание. Количество транспозиций в цикле может быть и больше четырех! Возьмем произвольную транспозицию из разложения этого цисла, например,. Тогда произведениесовпадает с тождественной перестановкой и циклможно представить в виде

или ,

или

.

Легко заметить, что во всех этих случаях число транспозиций четно и равно 4,6,8. Ясно, что способ «удлиняющий» разложение не изменяет четности исходного разложения.

Теорема. Пусть  – перестановка из , а

. (2.33)

какое-либо разложение  в произведении транспозиций. Тогда число

(2.34)

называется четностью (сигнатурой или знаком) перестановки  и полностью определяется , т.е. не зависит от способа разложения перестановки  в произведение траспозиций. Кроме того, если , то

. (2.35)

Данную теорему приводим без доказательства. Доказательство теоремы приведено в [1].

Определение. Перестановка называется четной, если , и нечетной, если .

Из определения четности перестановки вытекает, что все транспозиции – нечетные перестановки. Действительно, если – транспозиция, то, тогда

Следствие 1. Все четные перестановки степени n образуют подгруппу порядка (она называется знакопеременной группой степениn).

Следствие 2. Пусть перестановка разложена в произведение независимых циклов длин , где,, …,, …,– днины независимых циклов.

Тогда

. (2.36)

Доказательство. Действительно, по предыдущей теореме имеем . Кроме того,поскольку каждыйцикл записывается в виде произведениятранспозиций, то

.