Лекция 5 Циклические группы

Пусть g – произвольный элемент группы G. Тогда, принимая , мы получим минимальную подгруппу, порожденную одним элементом.

Определение. Минимальная подгруппа , порожденная одним элементом g группы G, называетсяциклической подгруппой группы G.

Определение. Если вся группа G порождена одним элементом, т.е. , то она называетсяциклической группой.

Пусть элемент мультипликативной группы G, тогда минимальная подгруппа, порожденная этим элементом, состоит из элементов вида

Рассмотрим степени элемента , т.е. элементы

.

Имеются две возможности:

1. Все степени элемента g различны, т.е. , то в этом случае говорят, что элемент g имеет бесконечный порядок.

2. Имеются совпадения степеней, т.е. , но.

В этом случае элемент g имеет конечный порядок.

Действительно, пусть, например, и, тогда,, т.е. существуют положительные степениэлемента, равные единичному элементу.

Пусть d – наименьший положительный показатель степени элемента , для которого. Тогда говорят, что элементимеет конечный порядок равный d.

Вывод. В любой группе G конечного порядка () все элементы будут конечного порядка.

Пусть g элемент мультипликативной группы G, тогда мультипликативная подгруппа состоит из всех различных степеней элемента g. Следовательно, число элементов в подгруппесовпадает с порядком элемента т. е.

число элементов в группе равно порядку элемента ,

.

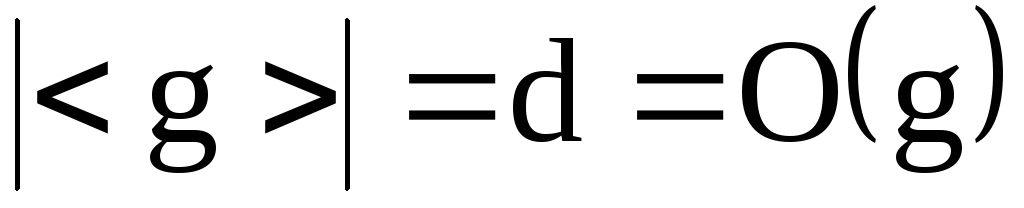С другой стороны, имеет место следующее утверждение.

Утверждение. Порядок любого элементаравен порядку минимальной подгруппы, порожденной этим элементом.

Доказательство. 1.Если – элемент конечного порядка , то

,

и если .

2. Если – элемент бесконечного порядка, то доказывать нечего.

Если элемент имеет порядок, то, по определению, все элементы

различны и любая степень совпадает с одним из этих элементов.

Действительно, пусть показатель степени , т.е.– произвольное целое число и пусть. Тогда числоможно представить в виде, где,. Тогда, используя свойства степени элемента g, получаем

.

В частности, если .

Пример. Пусть – аддитивнаяабелева группа целых чисел. Группа G совпадает с минимальной подгруппой порожденной одним из элементов 1 или –1:

и

,

следовательно, – бесконечная циклическая группа.

Циклические группы конечного порядка

В качестве примера циклической группы конечного порядка рассмотрим группу вращений правильного n-угольника относительно его центра .

Элементами группы

являются повороты n-угольника против часовой стрелки на углы

:

Элементами группы являются

При этом

,

а из геометрических соображений ясно, что

и

.

Группа содержитn элементов, т.е. , а образующим элементом группыявляется, т.е.

.

Пусть , тогда (см. рис. 1)

.

Рис. 1 – Группа – вращений правильного треугольника АВС относительно центра О.

Алгебраическая операция  в группе – последовательное вращение против часовой стрелки, на угол, кратный, т.е.

.

Обратный элемент – вращение по часовой стрелке на угол₁, т.е.

.

Таблица Кэли

Анализ конечных групп наиболее наглядно осуществлять с помощью таблицы Кэли, которая является обобщением известной «таблицы умножения».

Пусть группа G содержит n элементов.

В этом случае таблица Кэли представляет собой квадратную матрицу имеющую n строк и n столбцов.

Каждой строке и каждому столбцу соответствует один и только один элемент группы.

Элемент таблицы Кэли, стоящий на пересечении i-той строки и j-того столбца, равен результату выполнения операции «умножения» i-го элемента с j-тым элементом группы.

Пример. Пусть группа G содержит три элемента{g₁,g₂,g₃}.Операция в группе «умножение».В этом случае таблица Кэли имеет вид:

Замечание.  В каждой строке и каждом столбце таблицы Кэли находятся все элементы группы и только они. Таблица Кэли содержит полную информацию о группе.Что можно сказать о свойствах этой группы?

1. Единичным элементом этой группы является g₁.

2.Группа абелева т.к. таблица симметрична относительно главной диагонали.

3.Для каждого элемента группы существуют обратные-

для g₁обратным является элемент g_1,для g₂ элемент g_3.

Построим для групп таблицу Кели.

Для нахождения обратного элемента элементу, например, , необходимо в строке, соответствующей элементунайти столбецj содержащий элемент . Элементсоответствующий данному столбцу и является обратным к элементу, т.к..

Если таблица Кели симметрична относительно главной диагонали, то это означает, что

– т.е. операция в рассматриваемой группе коммутативна. Для рассматриваемого примера таблица Кели симметрична относительно главной диагонали это означает, что операция в коммутативна, т.е.,

а группа – абелева.

Можно рассматривать полную группу преобразований симметрий правильного n – угольника , добавив к операции вращения дополнительные операции пространственного поворота вокруг осей симметрии.

Для треугольника, а группа содержит шесть элементов

,

где это повороты (см. рис. 2) вокруг высоты, медианы, биссектрисы имеют вид:

;

,

, .

Рис. 2. – Группа – преобразований симметрии правильного треугольника АВС.