6. Свойства факторгрупп
Докажем
несколько теорем о простейших свойствах
факторгрупп.
Теорема 1. Каждая
факторгруппа
 абелевой группы G – абелева.
абелевой группы G – абелева.
Доказательство. Если
G – абелева группа, то

Теорема 2. Каждая
факторгруппа
 циклической группы G также циклическая.
циклической группы G также циклическая.
Доказательство. Пусть
G – циклическая группа, порожденная
элементом
 ,
H – некоторая подгруппа группы G и
,
H – некоторая подгруппа группы G и – произвольно выбранный элемент
факторгруппы
– произвольно выбранный элемент
факторгруппы .
.
Тогда
существует такое целое число
 ,
что
,
что и поэтому
и поэтому
Следовательно,
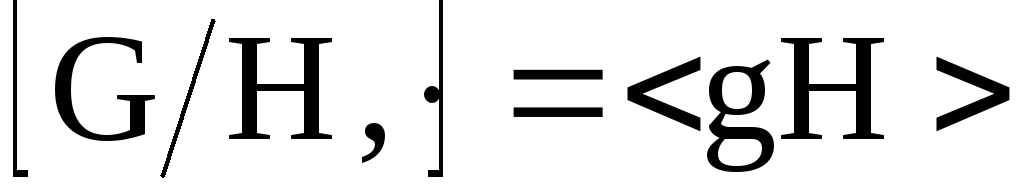 .
.
Теорема 3. Порядок
любой факторгруппы
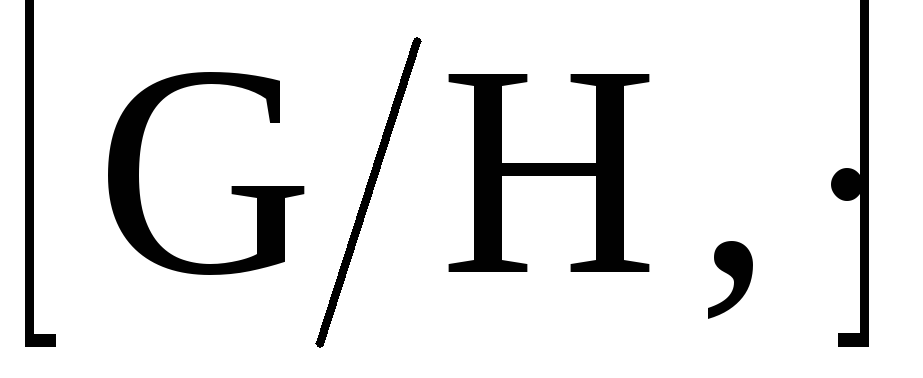 конечной группы
конечной группы порядка
порядка является делителем порядка этой группы.
является делителем порядка этой группы.
Доказательство. Действительно,
порядок факторгруппы
 равен индексу нормального делителя H в
группе G:
равен индексу нормального делителя H в
группе G:

 ,
,
т.е.
 делит
делит ,
где
,
где ,
, .
.


 абелевой группы G – абелева.
абелевой группы G – абелева. циклической группы G также циклическая.
циклической группы G также циклическая. .
.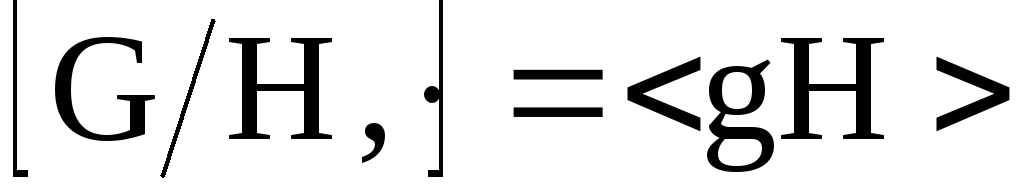 .
.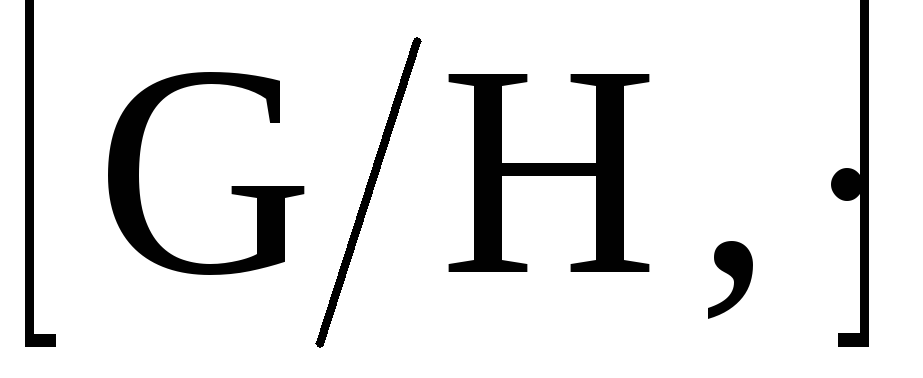 конечной группы
конечной группы равен индексу нормального делителя H в
группе G:
равен индексу нормального делителя H в
группе G: