Лекция 10 Обращение теоремы Лагранжа

 Теорема Лагранжа утверждает, что если , a, то

,

т.е. порядок любой подгруппы H группы G делит N – порядок группы G.

Естественно, возникает вопрос об обращении теореме: если m является делителем , то существует ли в группе G подгруппа H порядка m?

Другими словами: существует ли для каждого делителя m порядка группы N подгруппы H группы G порядка m?

В общем случае ответ отрицательный, однако в некоторых частных случаях такое обращение теоремы Лагранжа справедливо.

Теорема. (обращение теоремы Лагранжа)

1. Всякая подгруппа циклической группы есть снова циклическая группа.

2. Подгруппы бесконечной циклической группы исчерпываются бесконечными группами.

3. Подгруппы циклической группы порядка находятся во взаимно однозначном соответствии с положительными делителямичисла.

Доказательство. 

Докажем 1. Пусть – произвольная циклическая группа порядка. Для определенности будем предполагать, что– аддитивная группа.

В этом случае общий элемент группы имеет вид

.

Пусть – произвольная неединичная подгруппа группы, т.е..

Так как , то элементами подгруппыявляются элементы вида, но если.

Среди всех элементов вида , выберем элемент

, где – наименьшее положительное число.

Тогда любое можно представить в виде:

.

Из того, что

,

но m – наименьшее число, удовлетворяющее условию

mgH  r = 0  H =<mg>,

т.е. Н – циклическая группа с образующим элементом mg.

Докажем 2.  Подгруппы бесконечной циклической группы исчерпываются бесконечными группами.

Действительно, так как – циклическая группа с образующим элементом 1 или, т.е.

,

то, в соответствии с пунктом 1 данной теоремы, любая подгруппа H циклической группы определяется натуральным числоми имеет вид

,

причем все эти подгруппы бесконечны.

Докажем 3. Подгруппы циклической группы порядка находятся во взаимно однозначном соответствии с положительными делителямичисла.

Пусть, как и ранее, – аддитивная циклическая группа порядка, т.е.

.

Если , причем, если элемент

.

Нам надо доказать, что делит.

Действительно, представим

.

Тогда из того, что

,

а минимальность влечет, следовательно.

Таким образом, из того, что , следует, что подгруппаимеет порядок, т.е.

.

Когда пробегает по всем положительным делителям числа, то же самое делает и, и мы получаем ровно по одной подгруппе порядка, делящего.

Следствие. В циклической группе порядкаподгруппапорядкасовпадает с множеством элементов, таких, что.

Доказательство. Элементы циклической группе порядкаимеют вид

Если , тои.

Обратно, пусть и.

Из условия следует, что, откудаи.

1. Нормальные делители

Пусть G – произвольная группа, а H – подгруппа группы G, тогда, если то мы получаем два левых смежных классаи.

Мы хотим выяснить условия, при которых произведение элементов, взятых из смежных классов и, не зависит от выбора представителей классов и всегда принадлежит одному и тому же смежному классу, что и произведение элементов, а именно классу.

Элемент принадлежит смежному классу, а элемент– смежному классу.

Произвольные элементы, принадлежащие, соответственно, смежным классам иможно представить в виде:

Тогда их произведение

должно принадлежать классу

.

Это означает, что в подгруппе H,

Умножая почленно полученное равенство слева на , имеем:

(9)

где

Соотношение (9) позволяет сделать следующий вывод.

Так как элементы выбраны произвольно, то для любого элементаи любого элементасуществует элемент

,

удовлетворяющий соотношению (9).

Кроме того, элемент а элемент. В силу этого каждый левый смежный класс группы G по H содержится в некотором правом смежном классе группы G по той же подгруппе H:

Аналогично можно показать и обратное включение

а это будет означать, что

(10)

Определение 1. Подгруппа H группы G называется нормальным делителем или инвариантной подгруппой, если для любых двух смежных классов g₁H и g₂H по подгруппе H, произведение произвольных элементовиз этих классов, принадлежит одному и тому же смежному классу(рис. 2).

Рис. 2 – Подгруппа H – нормальный делитель группы G.

Формально: подгруппа H – нормальный делитель группы , если:

(11)

В коммутативных группах всякая подгруппа является нормальным делителем (в силу коммутативности операции сложения).

Для практического использования понятия нормального делителя рассмотрим еще несколько более «конструктивных в обращении» определений.

Определение 2. Подгруппа H группы G является нормальным делителем группы G в том и только том случае, если каждый левый смежный класс совпадает с правым смежным классомгруппы G по H и наоборот.

Формально: подгруппа H – нормальный делитель группы G, если:

(12)

Условие (12), очевидно, означает, что:

Примеры. 

1. В любой группе G сама группа и единичная подгруппаявляются ее нормальными делителями: левый и правый смежные классы группы G по подгруппесостоит из одного смежного класса, а левый (правый) смежные классы по единичной подгруппе H состоят из всех элементов группы G.

 

2. В каждой абелевой группе G каждая ее подгруппа H является нормальным делителем.

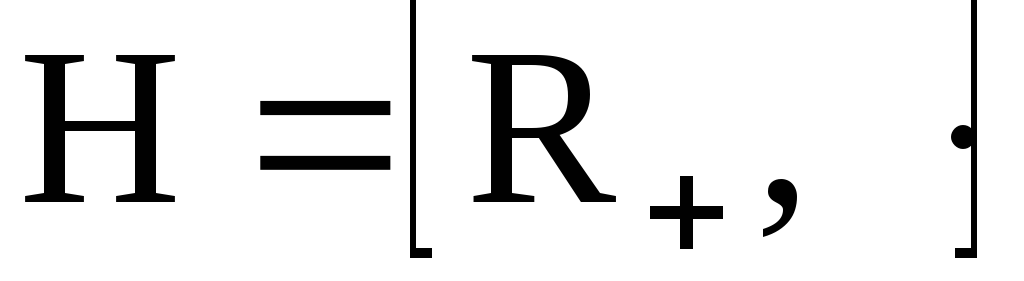3. Мультипликативная группа положительных вещественных чисел является нормальным делителем мультипликативной группы всех отличных от нуля вещественных чисел,

4. Мультипликативная группа отличных от нуля рациональных чисел является нормальным делителем мультипликативной группы отличных от нуля вещественных чисел

5. В мультипликативной группе невырожденных матриц-го порядка с вещественными коэффициентами подгруппаматриц с определителем равным единице:

является нормальным делителем этой группы.

Действительно, единичная матрица , если

кроме того

Далее, если то

и

– соответственно, левый и правый смежные классы группы -невырожденных матриц-го порядка с вещественными коэффициентами по подгруппе- матриц с определителем равным единице.

Если

,

т.е.

,

то

, т.е. .

С другой стороны, если

,

то

поскольку поэтому

Следовательно, сгруппировав в один смежный класс (левый или правый) все матрицы с равными детерминантами, получим разложение группы по подгруппе_. Этот пример показывает, что и в некоммутативных группах могут быть подгруппы – нормальные делители, для которых левый смежный класс

совпадает с правым смежным классом