4.1.3 Характеристика поля

Определение. Подполем поляназывается подкольцо всамо являющееся полем.

Например, поле рациональных чисел есть подполе поля вещественных чисел.

В случае, если , то говорят, что полеявляется расширением своего подполя, а поленазывается погруженным в поле. Из определения подполя следует, что нуль и еденицы полябудут содержаться так же ви служить длянулём и единицей.

Пусть – некоторое семейство подполей поля тогда имеет место следующие утверждение.

Теорема. Пересечение любого семейства подполейполябудет подполем в.

Доказательство. Доказательство этой теоремы аналогично доказательству аналогичного утверждения для колец.

Пусть, как и ранее, – некоторое подмножество множестваполя, такое, что оно содержится в каждом подполе семейства подполейт.е., тогда можно определить минимальное подполеполясодержащее заданное множество:

. (7)

Если взять пересечение , всех подполей, содержащихи некоторый элемент, не принадлежащий, тобудет минимальным полем, содержащим множество.В этом случае говорят, чтоминимальное расширение подполя поляполучено присоединением к полюэлемента, и отражают этот факт в записи.

Аналогично можно говорить о подполе поля, полученном присоединением к полюэлементовполя.

Пример. Поле чисел вида , гдеи– любые рациональные числа, является расширением полярациональных чисел: оно получается присоединением к полю рациональных чисел числаи поэтому может быть обозначено символом.

Определение. Поля иназываются изоморфными, если они изоморфны как кольца.

По определению, если – изоморфизм полейи, тои, где, а.

Замечание. Говорить о гомоморфизмах полей не имеет смысла, так как

.

Напротив, автоморфизмы, т. е. изоморфные отображения поля на себя связаны с самыми глубокими свойствами полей и являются мощным инструментом для изучения этих свойств в рамках так называемой теории полей Голуа.

Определение. Поле, не обладающее никаким собственным подполем, называется простым и обозначается .

Теорема. В каждом поле содержится одно и только одно простое поле. Это простое поле изоморфно либо, либо для некоторого .

Доказательство. 1. Предположим, что существует два различных простых подполя иполя. Это означает, что их пересечение(очевидно, не пустое поскольку 0 и 1 содержатся как в, так и), будет простым полем отличным оти, а это невозможно в виду их простоты. Следовательно, наше предположение неверно и простое полеединственно.

2. В простом поле наряду с единичным элементом 1, содержатся все его кратные

(4.8)

Из общих свойств операций сложения и умножения элементов в кольцах следует, что

(4.9)

. (4.10)

Следовательно, целочисленные кратные составляют некоторое целочисленное коммутативное кольцо.

Поэтому отображение кольца целых чиселв кольцо, определяемое правилом

(4.11)

является гомоморфизмом колец, ядро которого, будучи идеалом в , имеет вид

(4.12)

и состоит из тех целых чисел , которые отображаются в нуль, т.е. дают равенство. Согласно теореме о гомоморфизме, кольцоизоморфно кольцу классов вычетов, где– идеал кольца целых чисел.

Так как кольцо не содержит делителей нуля, следовательно, идеалдолжен быть простым. Кроме того, идеалне может быть единичным т.е., потому что иначе выполнылось бы равенство. Следовательно, есть только две возможности:

1. , где – простое число. В этом случаеявляется наименьшим положительным числом со свойством. Таким образом, кольцоизоморфно кольцу классов вычетов по модулю простого числат.е.

(13)

Кольцо для простогоявляется полем. Следовательно, кольцо– также поле, являющееся простым.

2. и . В этом случае гомоморфизмцелочисленных колец является изоморфизмом. В этом случае кольцоне является полем, потому что таковым не является кольцо целых чисел.

Простое поле должно содержать не только элементы из, в нем должны быть еще отношения этих элементов. Известно, что изоморфные целочисленные кольцаиимеют изоморфные поля частных, так что в этом случае простое полеизоморфно полю рациональных чисел.

Замечание. Действительно, если коммутативное кольцо, например, кольцо целых чисел – вложено в некоторое тело, то внутрииз элементов кольцаможно строить частные:

(4.14)

Таким образом частные составляют некоторое поле, которое называется полем частных коммутативного кольца, в данном случае, из кольца обычных целых чиселстроится поле рациональных чисел –.

Определение. Поле имеет характеристику нуль, если его простое подполе изоморфно; полеимеет (простую или конечную) характеристику, если оно изоморфно.

Характеристика поля обозначается, еслиимеет характеристику нуль и, еслиимеет конечную (простую) характеристику.

Замечание. Вместо для обозначения абстрактного поля из p элементов служит обычно(Galois Field – поле Галуа).

Следует заметить, что существует конечное поле с элементами, где – простое, а– любое целое положительное число.

Пример. Рассмотрим поле , состоящиеиз четырех элементовТаблицы Кэли для операций сложения и умножения в полеимеют вид:

	+	0	1					0	1
	0	0	1				0	0	0	0	0
	1	1	0				1	0	1
				0	1			0			1
				1	0			0		1

Чем являются элементы нас пока не интересует.

Иногда нулевую характеристику называют бесконечной в соответствии с ее интерпретацией как порядка единичного элемента 1 в аддитивной группе поля . Аналогично конечная характеристика– общий порядок любого ненулевого элемента в аддитивной группе поля:

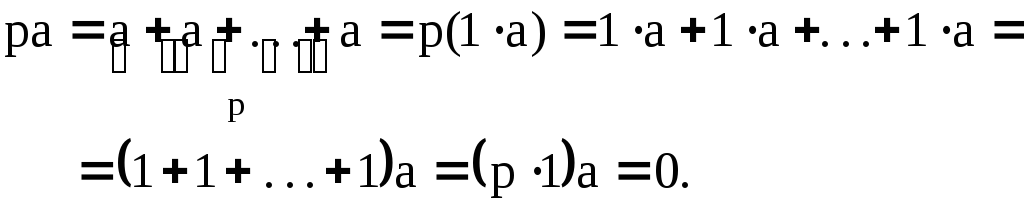(4.15)

Все числовые поля являются полями характеристики нуль. Все конечные поля являются полями конечной характеристики. Действительно, если поле – конечное, то среди всех целых положительных кратных единицеэтого поля обязательно будут кратные, равные между собой, в противном случае полебыло бы бесконечным. Пусть, где– некоторые натуральные числа, причем. Тогдаи, следовательно, поле– есть поле конечной характеристики.

Естественно возникает вопрос: каждое ли натуральное число может быть характеристикой некоторого поля ?

Ответ на этот вопрос следующий. Любое простое число , очевидно, является характеристикой поля. Другими словами, не существует полей, характеристиками которых были бы составные числа.

Теорема. Если поле имеет характеристику, то число– простое.

Доказательство. Доказательство будем вести от противного. Предположим, что – не простое число, тогда его можно представить в виде, гдеи.

Тогда имеем:

Это означает, что , но так как в полене существует делителей нуля, то из равенстваследует, что либолибо, но это противоречит условию, что полеимеет характеристику. Следовательно, предположение, что– составное число, неверно.

Рассмотрим элементарные свойства поля характеристики нуль и характеристики .

Теорема. Если – поле характеристики нуль, то любое целоекратное всякого отличного от нуля элементане равно нулю:.

Доказательство. Пусть – произвольный элемент поляотличный от нуля: , а– любое натуральное число. Тогда

Предположим, что т.е.. Так как в поленет делителей нуля и, по условию,, то из равенстваследует, что, а этого не может быть. Поэтому предположение, чтоневерное и, следовательно, при любом натуральномимеем. Более тогои при любом целом. Действительно, если элементи, то и противоположный ему элементполятакже был бы равен нулю, а этого по доказанному выше, не может быть.

Теорема. Если – поле характеристики, то для любого элементасправедливо равенство.

Доказательство. Действительно,

.