Лекция 17 Фактор-кольцо

Понятие идеала кольцааналогично понятию нормального делителя H для группы G . Это позволяет подойти к построению фактор-кольца таким же образом, как и при построении фактор-группы G/H.

Пусть – идеал кольца.

Так как основу кольца составляет аддитивная абелева группа , в качестве элементов фактор-кольца можно выбрать смежные классы, где, которые называютсяклассами вычетов по модулю идеала кольца.

Теорема. Множество аддитивных смежных классов образуют фактор-кольцо с операциями:

1. (1)

2. (2)

Кроме того, естественное отображение видаявляетсяэпиморфизмом (– сюрьективно).

Доказательство. В абелевой группе любая подгруппанормальна, т.к. , поэтому выражение (1) определяет абелеву группу фактор-кольца , а отображение является эпиморфизмом аддитивных абелевых групп G и.

Остается проверить, что выражение (2) однозначно определяет операцию умножения на множестве аддитивных смежных классов , т.е. не зависит от выбора представителей соответствующих классов.

Пусть ,- представители двух смежных классов и, т.е.

,

тогда , где .

Найдем произведение

,

где .

Остается показать, что .

Действительно, т.к. и – идеал в K, то ,

т.к. .

Поэтому находятся в одном смежном классе с элементами, а это означает что произведение (2) определено правильно.

Пример. Рассмотрим кольцо целых чисел . Идеалом этого кольца является, т.е. множество целых чисел, делящихся на m без остатка.

Аддитивный смежный класс кольца K по идеалу имеет вид , где.

Множество аддитивных смежных классов содержит ровно классов вычетов по модулю , и они имеют вид:

Таким образом, элементами фактор-кольца являются классы вычетов по модулю

.

Операции, на фактор-кольцезадаются на классах вычетов, как и ранее:

,

При фиксированном m будем, как и ранее, использовать сокращенные записи :

Понятие фактор-кольца по идеалу кольцапозволяет сформировать основную теорему о гомоморфизме колец.

Поле, определение, простейшие свойства.

В любом кольце выполняется операция вычитания – обратная операции сложения:

О выполнении операции деления – обратной операции умножения, в определении кольца не говорится ничего. Можно показать, что по отношению к операции деления различные кольца обладают различными свойствами. Например, в кольце четных чисел деление одного числа на другое выполняется только в исключительных случаях; в этом кольце нет ни одного элемента, на который делились бы все его элементы.

В кольце целых чи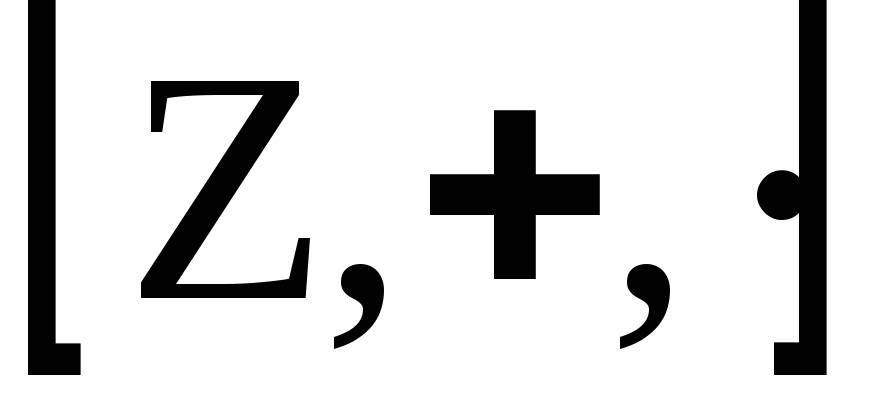сел деление одного числа на другое выполняется также в исключительных случаях, но все элементы этого кольца делятся на 1 и –1. В кольце рациональных чиселоперация деления выполняется всегда, кроме деления на нуль.

Замечание. Деление на нуль невозможно ни в каком кольце: разделить элемент на 0 – это значит найти в кольце такой элемент, что, но приэто невозможно, так как для любого элемента в кольце:.

В высшей алгебре в частности и в математике в целом особую роль играют коммутативные кольца, в которых выполняется операция деления, кроме деления на нуль. Их называют полями.

Дадим несколько определений поля, отражающих его основные особенности.

Определение 1. Коммутативное кольцо называетсяполем и обозначается , если в нем содержится, по крайней мере один, элемент, отличный от нуля, и если в нем выполняется операция деления, кроме деления на нуль, т.е. для любых его элементов и, из которых, в нем содержится, и притом только один, такой элемент, что:

(3)

Элемент называется частным элементовии записывается в виде дроби.

Определение 2. Полем называется коммутативное кольцо, у которого ненулевые элементы образуют группу относительно операции умножения:

–мультипликативная группа поля.

Определение 3. Поле – это коммутативное кольцо с единицей не равной нулю, в котором каждый отличный от нуля элемент обратим:

Как следует из определений, поле представляет собой гибрид двух групп – аддитивной абелевой группыи мультипликативной, связанных законом дистрибутивности (теперь уже одним, ввиду коммутативности).

Замечание. Требования, входящие в определение поля называются аксиомами поля.

Определение. Поля элементами которых являются числа, называются числовыми полями.

Примеры полей. 

1. Кольцо рациональных чисел является полем.

2. Кольцо действительных чисел также является полем.

3. Кольцо чисел вида, где, является полем.

4. Кольцо комплексных чисел является полем.

Все рассмотренные примеры являются числовыми полями. Примеры нечисловых полей будут рассмотрены ниже.