
КУРС АЛГЕБРА И ГЕОМЕТРИЯ / ЛЕКЦИИ АиГ / ЛЕКЦИЯ 11
.docЛЕКЦИЯ 11
Факторгруппа
Значение
нормального делителя в теории групп
основано на том, что из смежных классов
по нормальному делителю может быть
построена новая
группа.
Для построения такой группы определим
операцию умножения на множестве смежных
классов. Пусть
![]() ,
тогда
,
тогда
![]() (1)
(1)
Действительно, для
![]()
Пусть H – нормальный делитель группы G.
В этом
случае произведение двух смежных классов
G по H будет смежным классом по H.
Действительно,
![]() имеем:
имеем:
![]() (2)
(2)
Таким образом, на множестве всех левых смежных классов по нормальному делителю определена операция умножения. Это означает, что фактормножество
![]() . (3)
. (3)
является замкнутым относительно операции умножения смежных классов, а операция умножения смежных классов является алгебраической.
Равенство (2) показывает, что для нахождения произведения двух данных смежных классов группы G по нормальному делителю H надо в каждом из этих классов выбрать по одному представителю и потом взять тот смежный класс, к которому принадлежит произведение выбранных представителей.
В случае
если
![]() – абелева группа, бинарная операция на
фактормножестве
– абелева группа, бинарная операция на
фактормножестве
![]() вводится соотношением
вводится соотношением
![]() .
.
Теорема. Фактормножество
![]() смежных классов группы G по нормальному
делителю H с определенной в нем операцией
умножения является группой.
смежных классов группы G по нормальному
делителю H с определенной в нем операцией
умножения является группой.
Эта
группа называется факторгруппой группы
G по нормальному делителю H и обозначается
символом
 .
.
Доказательство. Для
доказательства покажем, что в
![]() будут выполнены все аксиомы группы:
будут выполнены все аксиомы группы:
-
ассоциативность умножения смежных классов следует из ассоциативности умножения подмножеств группы;
-
роль единицы играет сама подгруппа
 – нормальный делитель:
– нормальный делитель:
![]()
-
для смежного класса
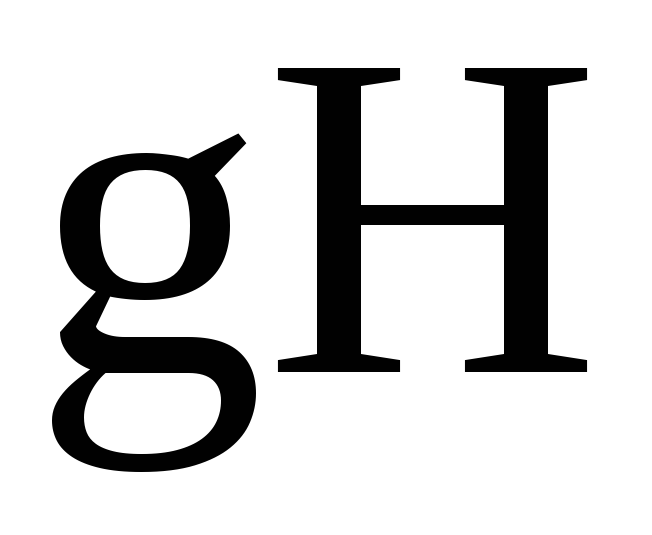 обратным является класс
обратным является класс
 действительно:
действительно:
![]()
Замечание.
Факторгруппу
![]() часто называют группой
часто называют группой
![]() по модулю
по модулю
![]() .
.
Выводы. Со всякой группой G связан целый набор новых групп – ее факторгрупп [G/H, ] по различным нормальным делителям.
Пример. 1. Пусть
![]() – аддитивная группа целых чисел, а
– аддитивная группа целых чисел, а
![]() – подгруппа целых чисел, делящихся на
m без остатка. Подгруппа
– подгруппа целых чисел, делящихся на
m без остатка. Подгруппа
![]() – нормальный делитель так как
– нормальный делитель так как
![]() – подгруппа аддитивной группы.
– подгруппа аддитивной группы.
Факторгруппа
![]() состоит из смежных классов
состоит из смежных классов
![]() – классов вычетов по модулю
– классов вычетов по модулю
![]() :
:
![]()

Каждым
двум классам
![]() и
и
![]() ,
независимо от выбора в них представителей
,
независимо от выбора в них представителей
![]() ,
,
![]() ,
можно поставить в соответствие классы,
являющиеся их суммой или произведением,
т.е. на множестве
,
можно поставить в соответствие классы,
являющиеся их суммой или произведением,
т.е. на множестве
![]() классов вычетов по модулю
классов вычетов по модулю
![]() однозначным образом индуцируются
операции сложения
однозначным образом индуцируются
операции сложения
![]() и умножения
и умножения
![]() по модулю
по модулю
![]() :
:
![]()
![]()
Пусть
![]() ,
тогда таблица Кэли для факторгруппы
,
тогда таблица Кэли для факторгруппы
![]() имеет вид:
имеет вид:
-

[0]5
[1]5
[2]5
[3]5
[4]5
[0]5
[0]5
[1]5
[2]5
[3]5
[4]5
[1]5
[1]5
[2]5
[3]5
[4]5
[0]5
[2]5
[2]5
[3]5
[4]5
[0]5
[1]5
[3]5
[3]5
[4]5
[0]5
[1]5
[2]5
[4]5
[4]5
[0]5
[1]5
[2]5
[3]5
Выводы:
-
Факторгруппа
 коммутативна – таблица Кэли симметрична
относительно главной диагонали.
коммутативна – таблица Кэли симметрична
относительно главной диагонали. -
Факторгруппа
 циклическая группа
циклическая группа
 .
Порядок этой группы равен 5. Одним из
бразующих элементов этой группы является
смежный класс
.
Порядок этой группы равен 5. Одним из
бразующих элементов этой группы является
смежный класс
 ,
а все остальные смежные классы совпадают
с его степенями. Так как порядок группы
равен 5, а 5-простое число, то в соответствии
с обращением теоремы Лагранжа она не
имеет собственных подгрупп.
,
а все остальные смежные классы совпадают
с его степенями. Так как порядок группы
равен 5, а 5-простое число, то в соответствии
с обращением теоремы Лагранжа она не
имеет собственных подгрупп.
Замечание.
1.Так
как операции на смежных классах сводятся
к соответствующим операциям над числами
из классов вычетов, то для фиксированного
![]() индекс
индекс
![]() можно опускать и вместо
можно опускать и вместо
![]() использовать символ
использовать символ
![]() .
В этом случае операции сложения
.
В этом случае операции сложения
![]() и умножения
и умножения
![]() классов вычетов по модулю
классов вычетов по модулю
![]() принимают вид
принимают вид
![]()
![]()
-
Высшим этапом освоения работы с классами вычетов по модулю
 является отказ от черточек и кружочков
в записи классов вычетов и операций
сложения
является отказ от черточек и кружочков
в записи классов вычетов и операций
сложения
 и умножения
и умножения
 .
В этом случае оперируют с каким-либо
фиксированным множеством представителей
классов вычетов по модулю
.
В этом случае оперируют с каким-либо
фиксированным множеством представителей
классов вычетов по модулю
 ,
чаще всего - с множеством
,
чаще всего - с множеством -
![]() .
.
Это
множество называется приведенной
системой вычетов по модулю
![]() .
.
В этом
случае операции сложения
![]() и умножения
и умножения
![]() классов вычетов по модулю
классов вычетов по модулю
![]() принимают вид:
принимают вид:
![]()
![]()
Пример 2. Пусть
![]() ,
тогда таблица Кэли для факторгруппы
,
тогда таблица Кэли для факторгруппы
![]() имеет вид:
имеет вид:
-
·
0
1
2
3
4
0
0
0
0
0
0
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
Замечание.
Как
следует из таблицы Кэли, множество
![]() не является группой, так как 0 не имеет
обратного элемента. Если исключить 0 из
множества
не является группой, так как 0 не имеет
обратного элемента. Если исключить 0 из
множества
![]() ,
тогда множество
,
тогда множество
![]() с операцией умножения по модулю 5 будет
группой, таблица Кэли для которой имеет
вид:
с операцией умножения по модулю 5 будет
группой, таблица Кэли для которой имеет
вид:

-
·
1
2
3
4
1
1
2
3
4
2
2
4
1
3
3
3
1
4
2
4
4
3
2
1
Порядок
группы
 равен 4. Группа циклическая с образующими
элементами 2 или 3 т. е.
равен 4. Группа циклическая с образующими
элементами 2 или 3 т. е.
 =<2>=<3>.
=<2>=<3>.
В соответствии с обращением теоремы Лагранжа делителями числа 4 являются 1, 2 и 4. Это означает, что данная группа имеет собственную подгруппу H второго порядка. Элементами этой подгруппы будут классы вычетов {1,4}, т.е.
![]() .
.
Таблица Кэли для этой подгруппы имеет вид:
-
·
1
4
1
1
4
4
4
1
Пример 3. Пусть
![]() .
Построим таблицы Кэли для факторгрупп
.
Построим таблицы Кэли для факторгрупп
![]() и
и
![]() .
.
![]()
-
+
0
1
2
3
0
0
1
2
3
1
1
2
3
0
2
2
3
0
1
3
3
0
1
2
![]()
-
·
0
1
2
3
0
0
0
0
0
1
0
1
2
3
2
0
2
0
2
3
0
3
2
1
Замечания.
1.
Факторгруппа
![]() является циклической группой с образующими
элементами 1 или 3 и имеет порядок равный
4, т.е.
является циклической группой с образующими
элементами 1 или 3 и имеет порядок равный
4, т.е.
![]() .
.
В
соответствии с обращением теоремы
Лагранжа делителями числа 4 являются
1, 2 и 4. Это означает, что данная группа
имеет собственную подгруппу H
второго
порядка. Элементами этой подгруппы
будут классы вычетов {0,2},
т.е.
![]() .
.
Таблица Кэли для этой подгруппы имеет вид:
-
+
0
2
0
0
2
2
2
0
3.
Множество
![]() также не является группой, так как 0 не
имеет обратного элемента. Исключая 0 из
множества
также не является группой, так как 0 не
имеет обратного элемента. Исключая 0 из
множества
![]() ,
получаем множество
,
получаем множество
![]() классов вычетов по модулю 4 без 0, таблица
Кэли для которого имеет вид:
классов вычетов по модулю 4 без 0, таблица
Кэли для которого имеет вид:
-
·
1
2
3
1
1
2
3
2
2
0
2
3
3
2
1
Анализ
таблицы Кэли показывает, что и в этом
случае множество
![]() классов вычетов по модулю 4 без 0 группой
не является т. к. содержит 0 и, следовательно
, множество
классов вычетов по модулю 4 без 0 группой
не является т. к. содержит 0 и, следовательно
, множество
![]() классов вычетов по модулю 4 без 0 не
замкнуто относительно операции умножения
по модулю 4.
классов вычетов по модулю 4 без 0 не
замкнуто относительно операции умножения
по модулю 4.
Свойства факторгрупп.
Докажем несколько теорем о простейших свойствах факторгрупп.
Теорема 1. Каждая
факторгруппа
 абелевой группы G – абелева.
абелевой группы G – абелева.
Доказательство. Если G – абелева группа, то
![]()
Теорема 2. Каждая
факторгруппа
 циклической группы G также циклическая.
циклической группы G также циклическая.
Доказательство. Пусть
G – циклическая группа, порожденная
элементом
![]() ,
H – некоторая подгруппа группы G и
,
H – некоторая подгруппа группы G и
![]() – произвольно выбранный элемент
факторгруппы
– произвольно выбранный элемент
факторгруппы
 .
.
Тогда
существует такое целое число
![]() ,
что
,
что
![]() и поэтому
и поэтому
![]()
Следовательно,
 .
.
Теорема 3. Порядок
любой факторгруппы
 конечной группы
конечной группы
![]() порядка
порядка
![]() является делителем порядка этой группы.
является делителем порядка этой группы.
Доказательство. Действительно,
порядок факторгруппы
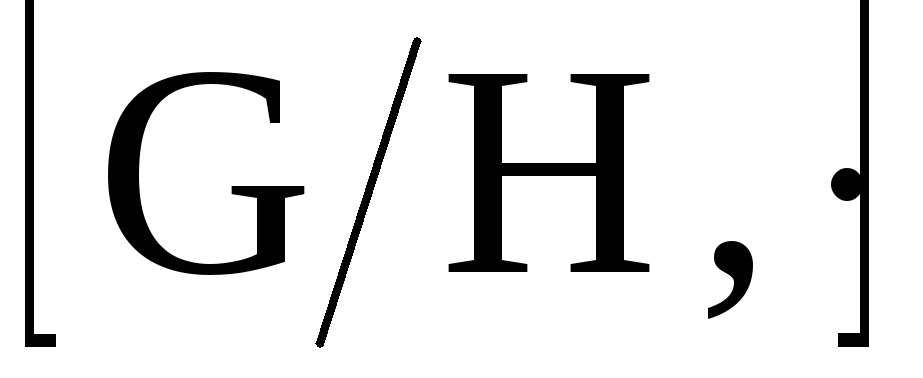 равен индексу нормального делителя H в
группе G:
равен индексу нормального делителя H в
группе G:
![]()
![]() ,
,
т.е.
![]() делит
делит
![]() ,
где
,
где
![]() ,
,
![]() .
.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
Пусть
![]() – аддитивная группа целых чисел, а
– аддитивная группа целых чисел, а
![]() – подгруппа целых чисел, делящихся на
m без остатка.
– подгруппа целых чисел, делящихся на
m без остатка.
Необходимо для заданного m:
1.Выписать
все элементы фактормножества
![]() .
.
2. Выписать
все элементы каждого класса вычетов по
модулю
![]() .
.
3.
Построить таблицы Кэли для факторгрупп
![]() и
и
![]() .
.
4.Определить
количество собственных подгрупп в
каждой из групп
![]() и
и
![]() ,
выписать все элементы каждой из подгрупп
и построить для них таблицы Кэли.
,
выписать все элементы каждой из подгрупп
и построить для них таблицы Кэли.
ПМ - m = 11
CA - m = 13
Инф - m = 7
