2. Кольцо многочленов

Пусть K – некоторое коммутативное кольцо.

Определение.  Стандартным многочленом (или полиномом) степени от переменной x над коммутативным кольцом K называется выражение вида

, (23)

где .

Элементы называются коэффициентами многочлена. Все они, или часть из них, могут быть нулевыми.

Каноническая форма многочлена (23) определяется следующим образом.

Находим наибольшее , такое, что, скажеми запишем

(24)

Степенью многочлена называется число , если оно существует. Если же всеобращаются в нуль, то канонической формой многочлена является 0, а его степень –. Степень обозначается .

Пусть и - два многочлена.

В зависимости от того, какому из множеств принадлежат коэффициенты , различаются следующие типы многочленов:

• с булевыми коэффициентами ;

• с целочисленными коэффициентами ;

• с вещественными коэффициентами ;

• с рациональными коэффициентами ;

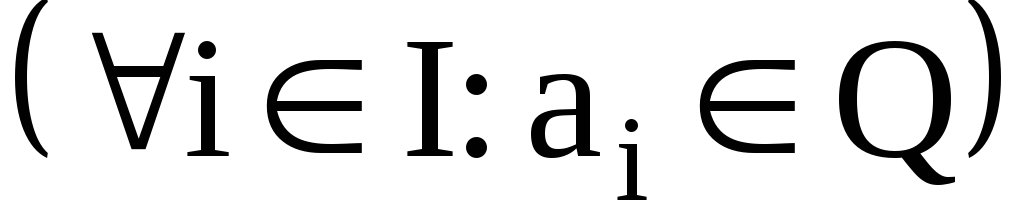• с комплексными коэффициентами .

Лемма. Многочлены иравны тогда и только тогда, когда, при которых определены, а все остальные, равны нулю.

Пусть имеется два многочлена степени истепени .

Определение. Суммой многочленов иназывается многочлен

(25)

где и

(26)

Определение. Произведением двух многочленов иназывается многочлен

, (27)

где .

Пример. Пусть заданы два многочлена с булевыми коэффициентами т.е. .

Суммой многочленов является многочлен вида:

,

а произведением – многочлен :

Можно показать, что введенная операция умножения многочленов ассоциативна, следовательно многочлены образуют по операции умножения полугруппу, и эта полугруппа коммутативна.

Вывод. Многочлены с целочисленными коэффициентами образуют коммутативное кольцо. Можно показать, что многочлены с рациональными, вещественными и комплексными коэффициентами также образуют соответствующие кольца многочленов. В общем случае говорят о «кольцах многочленов над кольцом.

3. Кольцо целостности.

Пусть – произвольное кольцо. Как было показано ранее, для любого элементавыполняются равенства:

.

Отсюда следует, что нулевой – 0 и единичный – элементы являются различными элементами кольца.

Если для элемента в кольцесуществует обратный элемент, то он единственный, для которого выполняется условие .

Единичный элемент кольца является обратным для самого себя:.

Из равенства следует, что элементтакже являетсяобратным для самого себя.

Нулевой элемент 0 кольца не имеет обратного элемента, поскольку , для любого элемента.

Определение. Элемент , для которого в кольцесуществует, и притом только единственный, обратный элемент , называют обратимым или делителем единицы.

Кольцо целых чисел является самым простым примером коммутативного кольца, в котором только 1 и –1 являются делителями единицы .

Теорема. Множество всех делителей единицыкольцаявляется группой по умножению.

Доказательство. Действительно, если , т.е. являются делителями единицы кольца, то

и, следовательно,

.

А это означает, что итакже являются делителями единицыи, следовательно, содержатся в множестве. Поэтому множествоявляется группой по умножению.

Определение. Группа называется группой делителей единичного элементакольца.

Так как для любого элемента выполняется равенство , то по определению делителей элементов кольца, каждый элемент является делителем нуля. В теории колец для произвольных элементовиспользуют следующее определение делителей нуля.

Определение. Элементы называются делителями нуля, если, а ; при этомназывают левым, а– правым делителем нуля.

Пример. 1. В кольце классов вычетов по mod m существуют делители нуля:

: ,

: .

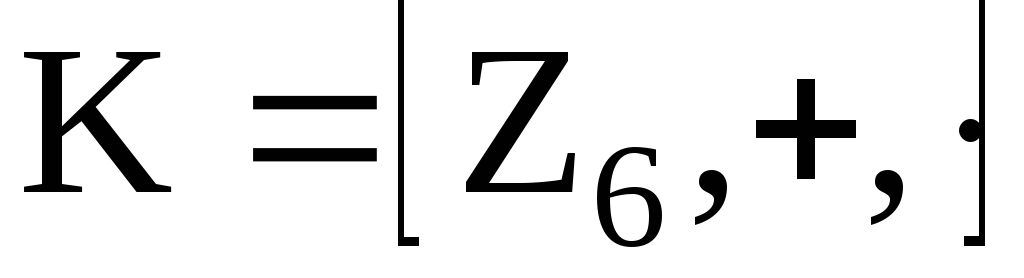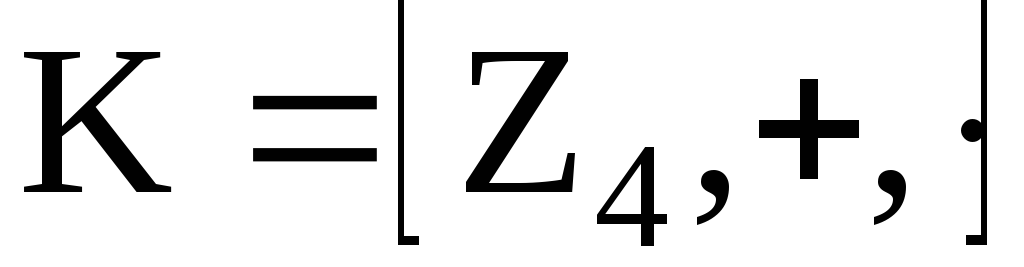2. В кольце квадратных матриц второго порядка также существуют делители нуля:

пусть ,

тогда .

Определение. Кольцом (областью) целостности называется коммутативное кольцо без делителей нуля.

Пример. 1. 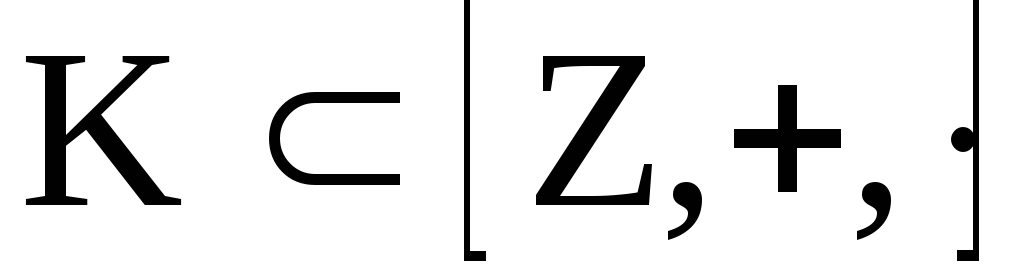– кольцо целых чисел является кольцом целостности.

2. Кольцо является кольцом целостности в том и только в том случае, если– простое число.

Рассмотрим произвольное кольцо 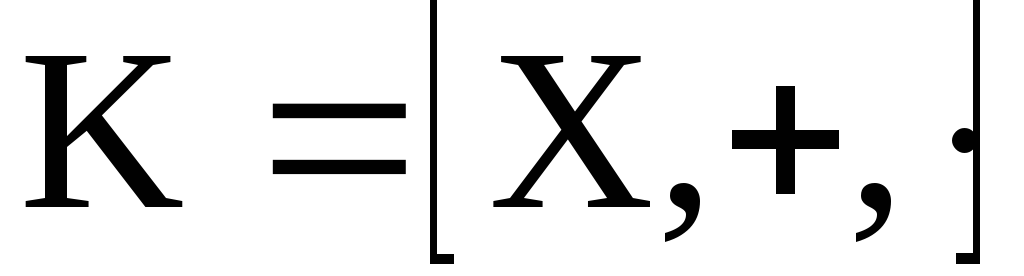. Если, и, т.е. кольцо не содержит делителей нуля, то такое кольцо называется телом. Более строго.

Определение. Кольцо K , в котором для всех отличных от нуля элементов существуют обратные, называется телом.

Тело не содержит делителей нуля, т.е. если и – тело, то, если.

Это означает, что отличные от нуля элементы тела образуют полугруппу по умножению.

Более того, т.к. тело содержит единичный элемент и для каждого отличного от нуля элемента в теле существует обратный элемент, то элементы тела, отличные от нуля образуют группу по умножению.

Примеры. 1. Тело рациональных чисел . Действительно, если , где.

Если .

Важно, чтобы обратный элемент .

Для любого целого числа, например , обратный элемент существует и равен, но он не принадлежит.

2. Тело вещественных чисел.

3. Тело комплексных чисел.

Кольцом целостности, с которым наиболее часто приходится встречаться, является кольцо целых чисел .

В теории колец особую роль играют кольца, которые по своим свойствам достаточно близки к кольцу целых чисел. В частности, для этих колец можно развить теорию делимости, аналогичную теории делимости целых чисел. Эти кольца получили название колец главных идеалов. Пусть – кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:

Определение.  Если для элементов кольца целостности всуществует такой элемент, что, то говорят, что элемент делится на, и пишут илиделит–, или.

Из определения делимости двух элементов вытекают следующие свойства делимости в кольце целостности:

1. 

2. 

3. 

4. 

Эти свойства являются распространением на кольцо целостности соответствующих свойств делимости в кольце целых чисел.

5. Каждый элемент делится на любой делительединицы. Действительно, если– делитель единицы, то и– также делитель единицы, а это означает, что, тогдаи, следовательно,.

6. Если делится на, тоделится и на, где– любой делитель единицы.

Действительно, из равенства следует равенствои, следовательно,.

7. Каждый элемент из делителей и, где– любой делитель единицы, является делителем и другого.

Действительно, из равенства следует равенство, а из равенства– равенство. Следовательно, если, то, и наоборот.

В дальнейшем будем рассматривать элементы кольца целостности , отличные от нуля.

Определение. Элементы кольца целостностиназываютсяассоциированными, если каждый из них является делителем другого:

. (55)

Из равенства (55) следует, что . Отсюда, сократив обе части полученного равенства на, получаем. Следовательно,иявляются делителями единицы. Таким образом, еслии– ассоциированные элементы, то, где– некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы, элементыиассоциированные между собой, поскольку.

Определение. Элементы кольца целостностиназываютсяассоциированными, если , где– некоторый делитель единицы.

Пример. В кольце целых чисел ассоциированными являются пары чисел.

Если иассоциированные элементы кольца целостности, то. Отсюда следует, что– главный идеал, порожденный элементомявляется подмножеством– главного идеала, порожденного элементоми наоборот:

Это означает, что два ассоциированных элемента , кольца целостностипорождают один и тот же главный идеал.

Пусть – произвольные элементы кольца целостности.

Определение. Элемент называется общим делителем элементови, если каждый из этих элементов делится на.

По свойству 5 все делители единицы кольца целостностиявляются общими делителями элементови. Но у элементовимогут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называютнаибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности нет отношения порядка. Однако можно ввести и другое определение НОД двух чисели, а именно: НОД двух чиселиназывается такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности.

Определение. Наибольшим общим делителем двух элементов кольца целостностиназывается такой элемент, обозначаемый символоми обладающий двумя свойствами:

1. ;

2. .

Замечание. Ясно, что вместе с свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если– НОД элементов, то формально это записывается в видеили. Если также и, то элементыиделятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если, то, очевидно,, где– любой делитель единицы. Таким образом НОД элементовопределяется с точностью до сомножителя, который является делителем единицы.

С учетом этого замечания к свойствам 1., 2. Наибольшего общего делителя добавляются следующие:

3. ;

4. ;

5. ;

6. .

Свойство 6. позволяет распространить понятие НОД на произвольное конечное число элементов кольца целостности .

По аналогии с вводится дуальное понятиенаименьшего общего кратного элементовкольца целостностиопределенного с точностью до ассоциированности и обладающее также двумя свойствами:

;

.

В частности, полагая , получаем, что.

Теорема. Если для элементов кольца целостностисуществуюти. Тогда

а) ;

б) ,.

Доказательство. Утверждение а) вытекает непосредственно из определения . Для доказательства б) необходимо убедиться, что элемент, определенный равенством, обладает свойствами 1., 2. НОД. Действительно, из, следовательно, откуда после сокращения на, допустимого в любом кольце целостности, имеем, т.е.. Аналогично, т.е.. Этим доказано свойство 1. Для доказательства свойства 2. Представим. Положим. Тогда– общее кратное элементови. Согласно свойствудля некоторого, откуда, т.е.и, что и требовалось доказать.

Определение. Элементы кольца целостностиназываются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД.

Пусть – произвольный делитель единицы, и– произвольный элемент кольца целостности. Тогда из условияследует, что. Это означает, что все элементы ассоциированные с элементом, и все делители единицы являются делителями элемента. Их называюттривиальными или несобственными делителями элемента . Все делители отличные оти, если такие существуют в, называютсянетривиальными, или собственными делителями элемента .

Пример. В кольце целых чисел тривиальными делителями числа 10 являются числаи, а нетривиальными – числаи.

Определение. Элемент кольца целостностиназывается неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элементназывается разложимым, или составным, если он имеет нетривиальные делители.

Другими словами, элемент называется разложимым, если его можно представить в виде произведениядвух нетривиальных делителей; элемент– называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.

Пример. В кольце целых чисел неразложимыми являются числат.е. простые числа и противоположные простым. Все остальные числа отличные от, – разложимы.

Неразложимые элементы обладают следующими свойствами:

• если элемент кольца целостностинеразложимый, то и любой ассоциированный с ним элементтакже неразложимый;

• если – произвольный элемент кольца целостности, а– неразложимый элемент из, то илиделится на, илии– взаимно простые элементы из.

Действительно, первое свойство следует непосредственно из свойства 7 делимости элементов кольца целостности. Второе свойство докажем следующим образом. Если НОД, токак делитель неразложимого элемента, является либо некоторым делителем единицы, либо элементом вида. В первом случае элементыивзаимно простые, во втором –делится на.

Определение. Кольцо целостности называется кольцом с однозначным разложением на простые множители ( или факториальным кольцом), если любой элементизможно представить в виде:

, (46)

где обратный элемент, а– простые элементы (не обязательно попарно различные), причем из существования другого такого разложения

следует, что и при надлежащей нумерации элементовибудет

,,…,,

где – обратные элементы в. Допуская в разложении (46), мы принимаем соглашение, что обратимые элементыв кольце целостноститакже имеют разложение на простые множители. Ясно, что если– простой, аобратный элемент в, то ассоциированный сэлементтоже простой.

Пример. В кольце целых чисел с обратимыми элементамииотношение порядкадает возможность выделитьположительное простое число из двух возможных простых элементов.

Теорема. Пусть – произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в(факториальность) имеет место тогда и только тогда, когда любой простой элемент, делящий произведение, делит по крайней мере один из сомножителейили.

Доказательство. Пусть . Если

разложения на простые множители, а– кольцо с однозначным разложением, то из равенствследует, что элементассоциирован с одним изили, т.е.делитили.

Обратно, установим однозначность разложения в , гдеили. Рассуждая по индукции, допустим, что разложение всех элементов изс числомпростых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).

Докажем теперь это для любого элемента , который может быть разложен напростых сомножителей. Именно, пусть

(47)

– два разложения элемента с.

Условие теоремы, примененное к дает нам, чтодолжен делить один из элементов. Без ограничения общности (это вопрос нумерации) будем считать, что. Но– простой элемент, поэтому, где – обратимый элемент. Используя закон сокращения в , получаем из (41) равенство

. (48)

В левой части равенства (42) стоит произведение простых сомножителей. По предположению индукциии оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.

Замечание. В произвольном кольце целостности элементвообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.

Пример. Рассмотрим кольцо целостности , где.

Норма каждого отличного от нуля элемента– целое положительное число. Если элементобратим в, то, откуда. Это возможно лишь при . Таким образом в , как и в 1, обратимыми элементами являются только. Если, то. Так как, то при заданномчисло множителейне может неограниченно расти. Следовательно, разложение на простые множители ввозможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:

.

Неассоциированность элементов 3 и очевидна. Далее,. Поэтому из разложениядляилис необратимымиследовало бы, т.е., что невозможно, поскольку уравнениеснеразрешимо. Этим доказана простота элементов 3 и.