Лекция 9

Теорема.1. Два левых смежных класса группы G по подгруппе H совпадают или не имеют общих элементов.

2.Разбиение группы G на левые смежные классы по подгруппе H определяет на G отношение эквивалентности.

,

причем

.

Доказательство. 2 Полученное разбиение индуцирует на G отношение эквивалентности, которое определяется следующим образом.

(1)

Выражение (1) есть не что иное, как условие совпадения классов и,если.

Убедимся, что условие (1) определяет отношение эквивалентности на G.

Для этого необходимо показать, что для (1) выполняются:

1. рефлексивность

;

2. симметричность

;

3. транзитивность

.

Действительно

Замечание. 

1. Если G – конечная группа, например, ,

,

то любые два смежных класса группы G по H исодержат одинаковое количество элементов, а именно

.

2. Смежные классы не являются подгруппами G, за исключением самой подгруппы H, т.к. не содержат e.

Пример. Пусть G – аддитивная группа векторов на плоскости, т.е.

.

В качестве подгруппы выберем ось OX, т.е., тогда для произвольного, но фиксированного элементалевый смежный класс группыпо подгруппеимеет вид:

.

Если вектор h пробегает всю ось OX, то конец вектора пробегает всю прямую параллельную оси OX и проходящую через конец вектора g (рис. 1).

Рис. 1 – Левый смежный класс аддитивной группы векторов на плоскости.

Определим класс эквивалентности

.

Вывод. Класс эквивалентности, это веер векторов, концы которых лежат на прямой параллельной оси OX.

Отождествляя векторы с их концами можно сказать, что класс эквивалентности – это прямая параллельная оси OX, а вся группа G (плоскость) разбивается на совокупность параллельных прямых.

Т.е. каждому левому смежному классу группы по подгруппе соответствует прямая параллельная оси OX. Количество таких левых смежных классов бесконечно.

1. Сравнение целых чисел по модулю m

Определение. Два целых числа сравнимы между собой по, если их разность делится набез остатка:

.

Лемма 1. 

Сравнение по - есть отношение эквивалентности.

Доказательство. Для доказательства проверим выполнение аксиом отношения эквивалентности:

• рефлексивность :

;

• симметричность

• транзитивность .

.

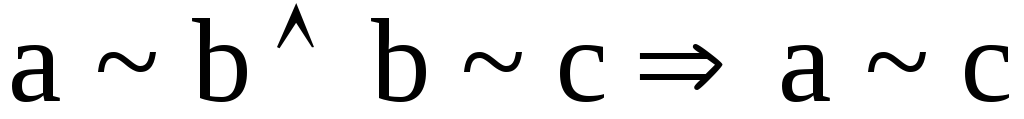Лемма 2. Если иимеют при делении наодинаковые остатки, то они сравнимы по модулю.

Доказательство .Представим а и b в виде

.

Лемма 3. Если , тогда при делении начисладают одинаковые остатки.

Доказательство.

Из

.

Представим а и b в виде

, , где,.

Тогда

.

Это означает, что разность делится на, но

и ,

а так как делится на, то.

2. Разложение аддитивной группы целых чисел на множество классов вычетов по модулю m

Рассмотрим аддитивную абелеву группу целых чисел

,

где , причем– простое число.

При делении любого целого числа на существует ровноостатков,

,

а каждому остатку соответствует свой класс эквивалентности:

.

т. е. левый смежный класс группы по подгруппе

Количество таких классов совпадает с количеством остатков при делении любого целого числа на , т. е. равно.

Выпишем эти классы.

,

– числа, делящиеся на без остатка;

,

– числа, дающие при делении на остаток 1.

,

– числа, дающие при делении на остаток 2.

,

– числа, дающие при делении на m остаток .

Таким образом, аддитивную группу целых чисел можно представить в виде объединения m непересекающихся левых смежных классов:

. (2)

Определение. Классы вычетов по модулю m – это левые смежные классы аддитивной группы целых чисел по подгруппе, а разложение (2) является разложением аддитивной группы целых чисел на классы вычетов по модулю.

.

Замечание. Несмотря на то, что аддитивная группа целых чисел и ее собственная подгруппабесконечны, количество классов вычетов по модулю m конечно и равно m.