Экстраполятор нулевого порядка

Очевидно, что функцией этого экстраполятора является поддержание выходной величины в промежутке времени от дона фиксированном уровне.

На схемах экстраполятор нулевого порядка обозначается . Рассмотрим фрагмент цифровой системы, представленный на рис.12.

Рис.12. Фрагмент цифровой системы

Форма входного, промежуточного и выходного сигналов этого фрагмента системы приведены на рис.13.

а)	б)	в)
Рис.13. Входной, промежуточный и выходной сигналы цифровой системы с экстраполятором 0-го порядка

Функция представляет собой передаточную функцию экстраполятора нулевого порядка.

Примечание. Передаточной функцией линейного динамического элемента называется отношение преобразования Лапласа выходных и входных сигналов этого элемента. Существует однозначная зависимость между дифференциальными уравнениями, описывающими динамику элемента, и его передаточной функцией.

Очевидно, что на промежутке времени , где, экстраполятор нулевого порядка должен формировать единичный прямоугольный импульс (рис.14), который может быть представлен следующей разностью:

.

Тогда преобразование Лапласа выходного сигнала экстраполятора 0-го порядка будет иметь следующий вид:

.

Преобразование Лапласа входного сигнала, соответствующего - функции, равно:

.

Таким образом, передаточная функция экстраполятора 0-го порядка примет вид:

=		.

Рис.14. Выходной сигнал экстраполятора 0-го порядка для

Определим спектральные характеристики экстраполятора нулевого порядка, осуществив замену: .

Комплексная спектральная характеристика экстраполятора 0-го порядка:

.

Амплитудная и фазовая характеристики экстраполятора 0-го порядка соответственно равны (рис.15):

,
.

Рис.15. Амплитудная и фазовая характеристики экстраполятора 0-го порядка

Экстраполятор первого порядка

Этот элемент основан на линейной экстраполяции функции в промежутке временина основе значенийи.

Выходной сигнал экстраполятора первого порядка (с коррекцией скорости изменения), соответствующий его реакции на входной импульс , представлен на рис.16.

Рис.16. Форма выходного сигнала экстраполятора 1-го порядка

Действительно, в соответствии с ранее рассмотренным уравнением экстраполятора 1-го порядка его выходной сигнал в различные промежутки времени можно представить следующим образом:

.

Очевидно, что преобразование Лапласа такого сигнала имеет вид:

.

Передаточная функция экстраполятора 1-го порядка равна:

=	ℒ	.
	ℒ

Определим спектральные характеристики экстраполятора первого порядка, осуществив замену: .

Комплексная спектральная характеристика экстраполятора 1-го порядка:

.

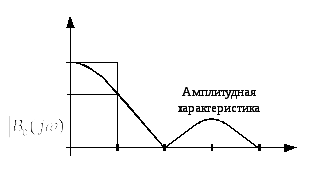
Амплитудная и фазовая характеристики экстраполятора 0-го порядка соответственно равны (рис.17):

,
.

Рис.17. Амплитудная и фазовая характеристики экстраполятора 1-го порядка
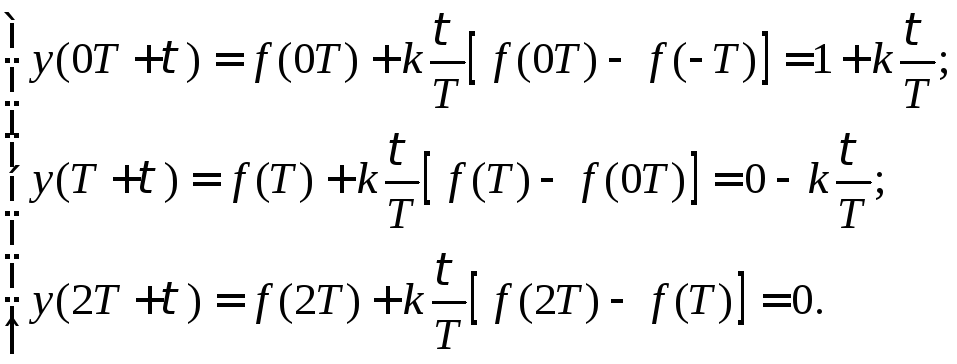
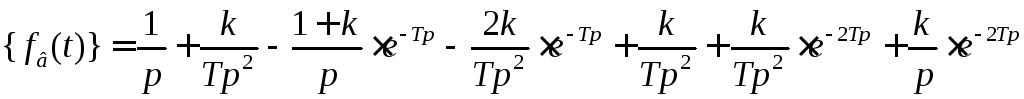