Lektsia_06_new_MS_end

МАТЕМАТИЧЕСКАЯ

СТАТИСТИКА

ЛЕКЦИЯ 13, 14

РАЗДЕЛ 6

ОСНОВЫ РЕГРЕССИОННОГО АНАЛИЗА

6.01. Исходные предположения

6.02. Метод наименьших квадратов

6.03. Статистический анализ регрессионной модели

6.04. Выбор допустимой модели регрессии

1

6.01. Исходные предположения

После обнаружения стохастических связей между изучаемыми переменными величинами (см. тему 5) исследователь приступает к математическому описанию интересующих его зависимостей. Для достижения этой цели ему необходимо решить следующие задачи:

–подобрать класс функций, в котором целесообразно искать наилучшую (в определенном смысле) аппроксимацию искомой зависимости;

–найти оценки для неизвестных значений параметров, входящих в уравнение искомой зависимости;

–установить адекватность полученного уравнения искомой зависимо-

сти;

–выявить наиболее информативные входные переменные (факторы). Совокупность перечисленных задач и составляет предмет исследова-

ний регрессионного анализа.

Во многих прикладных задачах требуется построить математическую модель, связывающую входные переменные (факторы) X1, …, Xp и выход-

ное переменное (отклик) Y . В дальнейших рассуждениях будем предполагать, что Y является случайной величиной при каждом фиксированном на-

боре x =(x1, …, xp ) значений переменных X =(X1, …, Xp ) . В этом случае

искомая математическая модель может быть представлена в следующем виде:

где f (x) – скалярная функция, ε(x) – случайная ошибка, т.е. случайная составляющая, порожденная либо действием случайных факторов, не включенных в набор X1, …, Xp , либо случайными ошибками измерений величины f (x) , либо и тем и другим одновременно.

Будем считать, что для каждого x математическое ожидание ε(x) равно нулю, т.е. отсутствует систематическая погрешность модели. Следовательно, для условного математического ожидания y(x) = M(Y|X = x) вы-

ходного переменного Y при условии, что вектор входных переменных X принял значение x , согласно (6.1), имеем y(x) = f (x) .

2

Функцию f (x) , описывающую зависимость условного среднего значения y(x) выходного переменного Y от заданных фиксированных значений

входных переменных X1, …, Xp , называют функцией регрессии (или регрес-

сией).

Функция регрессии полностью определена, если известен условный за-

кон распределения выходного переменного Y при условии, что X = x . Поскольку в реальных ситуациях никогда не располагают такой информацией,

но организованного эксперимента.

Говоря о подходящей аппроксимации функции f (x) – модели регрессии,

нужно, во-первых, задать класс допустимых моделей регрессии F , т.е.

класс функций, среди которых будем искать наилучшую аппроксимирующую функцию fa (x) , и, во-вторых, выбрать критерий, по которому будем полу-

чать наилучшую аппроксимирующую функцию fa (x) из заданного класса F .

тельная функция аргумента как правило, неубывающая и выпуклая, например ρ = u2 или ρ = u .

Функцию fa (x) считают наилучшей аппроксимирующей функцией из за-

данного класса F , если она обеспечивает минимальное значение функционала

где усреднение проводится по всем возможным значениям случайного вектора X в первом равенстве и по всем имеющимся наблюдениям – во вто-

принято называть методом наименьших квадратов (МНК). Далее будем рассматривать только этот тип регрессии. Поэтому, говоря о регрессии, будем опускать слова “средняя квадратичная”.

В дальнейшем будем предполагать, что класс F допустимых моделей регрессии можно задать некоторым параметрическим семейством функций,

наилучшей аппроксимации для f (x) сводится к определению таких значений

параметров β , при которых n (fa ) достигает минимума.

Следует отметить, что проблема выбора параметрического семейства функций являясь ключевой в регрессионном анализе, не имеет, к сожалению, формализованных процедур для своего решения. Иногда выбор опре-

деляют на основе экспериментальных данных (x i, yi ) , i =1, n , чаще – из

теоретических соображений.

Например, если известно, что скорость протекания химической реакции между некоторыми компонентами пропорциональна объему исходного вещества, то объем вещества V(t) в момент t изменяется по экспоненциальному закону

V(t) = θ0e−θ1 (t−t0 ) , t >t0 ,

где θ0 , θ1 – неизвестные параметры модели, которые нужно оценить наи-

лучшим образом по результатам наблюдений, а t0 – начальный момент

времени.

К сожалению, такие случаи редки. Более реальной является ситуация, когда о механизме явления ничего не известно и можно лишь предполагать, что искомая функция f (x) является достаточно гладкой. Тогда аппроксими-

рующая ее функция fa (x) может быть представлена в виде линейной комби-

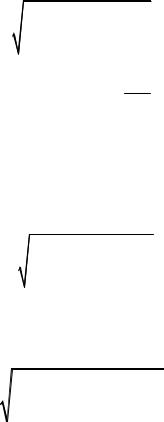
нации некоторого набора линейно независимых базисных функций {ψk (x)} , k = 0, m −1 , т.е. в виде

Следует заметить, что, согласно (6.2), функция fa (x) = fa (x; β) является

линейной по параметрам, представленным вектором β . Поэтому в рассмат-

риваемом случае говорят о модели, линейной по параметрам.

Другими словами, исходный класс функций F , содержащий истинную функцию регрессии f (x) , заменяют некоторым классом Fβ = {fa (x; β)} ,

β m , более простых по структуре функций, представимых в виде (6.2), и задача сводится к наилучшей оценке вектора неизвестных параметров

β =(β0, β1, …, βm−1)T .

При такой постановке задачи общая погрешность

n

=∑(yi − fa (x i ))2

i=1

от аппроксимации результатов наблюдений

полученных в эксперименте, значениями функции fa (x) Fβ обусловлена

рассеянием отклика Y относительно истинной регрессии f (x) , т.е. величиной

n

ε = ∑(yi − f (x i ))2

i=1

исистематической погрешностью аппроксимации, связанной с заменой ис-

ходного класса функций F более узким Fβ F :

n

a = ∑(f (x i ) − fa (x i ))2 .

i=1

5

Следовательно, приближение f (x) ≈ fa (x; β) (см. 6.2) нужно понимать в том смысле, что систематической погрешностью a при замене класса F

на Fβ можно пренебречь по сравнению со случайной погрешностью ε .

Именно на сопоставлении этих двух типов погрешностей и основаны прави-

ла проверки адекватности модели fa (x; βˆ) = fˆa (x) , где вектор параметров β

заменен значением вектора оценок βˆ .

Одним из наиболее распространенных аппроксимирующих классов функций Fβ является класс полиномов, в котором в качестве базисных

функций выбраны степени переменных x1, …, xp .

Простейшей полиномиальной моделью является модель 1-го порядка, линейная по всем переменным:

m−1

fa (x) = ∑βkxk , m ≤ p +1

k=0

где x0 ≡1 – фиктивное переменное, т.е. здесь ψ0(x) ≡1 , ψ1(x) = x1 , …,

ψm−1(x) = xm−1 .

Следует подчеркнуть, что представление (6.2) является самым общим видом линейной по параметрам модели и описывает не только полиноми-

альные модели. Например, в качестве базисных функций ψk (x) могут высту-

пать тригонометрические функции sin kx , cos kx , показательные ekx и др. Если неизвестная функция регрессии f (x) представлена в виде (6.2), то

задача ее поиска сведена тем самым к оценке вектора неизвестных параметров β =(β0, β1, …, βm−1)T и последующей проверке качества аппроксима-

ции f (x) ≈ fa (x) , т.е. адекватности модели fa (x) . Если модель (6.2) окажется неадекватной, то вид аппроксимирующей функции fa (x) нужно уточнять ли-

бо увеличением числа m базисных функций, либо заменой самих базисных функций другими, более подходящими.

Матричная форма записи линейной регрессионной модели. Резуль-

таты эксперимента для исследования связи между откликом Y и вектором

где x i =(x1i, …, xpi ) , i =1, n , – различные значения вектора факторов X , для которых проводился эксперимент; ri – число независимых повторных (па-

образованную двумя первыми строками матрицы D , называют часто планом эксперимента, совокупность возможных значений вектора факторов X

называют факторным пространством и обозначают Xp .

Если на основе системы равенств (6.4), которая содержит в себе всю информацию, полученную в эксперименте, мы сумеем оценить неизвестные

параметры βk (некоторым наилучшим образом), т.е. сумеем найти значения

7

βˆk ≈ βk , то тем самым будет найдена наилучшая (для выбранных базисных функций) модель следующего вида:

занной с выбором класса аппроксимирующих функций Fβ (если удачно по-

добрать как сами функции ψk (x) , так и их количество m ).

Таким образом, модель (6.5) требует в общем случае проверки на адекватность (на соответствие результатам эксперимента) и при необходимости уточнения (это рассмотрено ниже, см. п. 6.3).

Введем в рассмотрение следующие матрицы:

– матрицу отклика Y =(Y1, …,Yn )T типа n ×1 , если повторных опытов

не было (т.е. ri =1 , i =1, n ), или матрицу выборочных средних значений отклика Y типа n ×1 в противном случае, i -й элемент которой есть:

тор-столбец β =(β0, …, βm−1)T параметров модели.

Тогда систему равенств (6.3) можно представить в матричном виде:

Уравнение (6.6) называют линейной регрессионной моделью. Подчерк-

нем, что линейность в этой модели понимается как линейность по парамет-

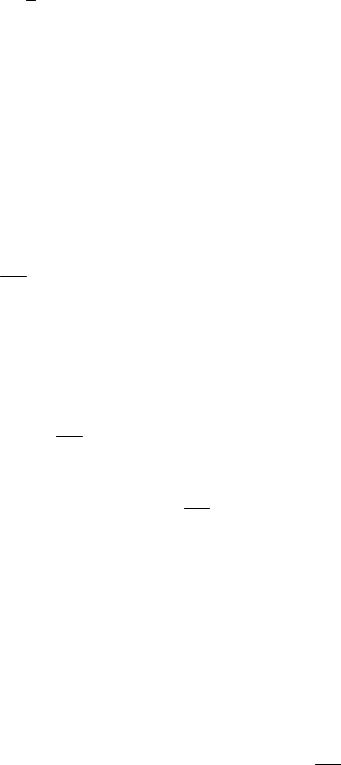
8

рам β0, β1, …, βm−1 , называемым также коэффициентами регрессии. По пе-

ременным X1, …, Xp модель (6.6) может быть (и, как правило, так и бывает)

нелинейной.

При наличие повторных опытов в равенстве (6.6) вместо матрицы Y будет стоять матрица Y .

6.02. Метод наименьших квадратов

Матрицы F и Y в линейной регрессионной модели (6.6) содержат всю информацию, получаемую в результате эксперимента. По этим данным нам

нужно оценить вектор неизвестных параметров β =(β0, β1, …, βm−1)T . Для

получения оценок, как отмечалось выше, будем использовать метод наименьших квадратов. Предварительно сформулируем предположения, лежащие в его основе.

1. Mεi = 0 , i =1, n , т.е. систематическая погрешность модели отсутствует.

2. M(εiεj ) = 0 , i ≠ j , т.е. случайные ошибки некоррелированы (это огра-

ничение можно снять, если матрица ковариаций Dε вектор-столбца ошибок известна).

3. Dεi = Mεi2 = σ2 , i =1, n , т.е. в любых точках факторного пространства

Xp случайные ошибки имеют одинаковую дисперсию.

4. Значения xi переменных Xi , i = 1, p , в процессе эксперимента изме-

ряются без ошибок.

Отметим, что предположения 2 и 3 можно объединить и представить в следующем виде:

Dε = σ2In ,

где In – единичная матрица порядка n .

Четвертое предположение означает, что, согласно соотношениям (6.3), верны равенства

m−1

MYi = ∑βk ψk (x i ) , DYi = Dεi = σ2 , i = 1, n , k=0

9

которые в матричной записи имеют вид

MY = Fβ , DY = σ2In .

Подчеркнем, что никаких предположений о законе распределения слу-

чайных величин Yi , i = 1, n , мы пока не делаем.

Теорема 6.1. Пусть M = FT F – невырожденная матрица. Несмещенной эффективной оценкой в классе всех линейных оценок для параметра

β =(β0, β1, …, βm−1)T в линейной регрессионной модели (6.6) является оцен-

ка метода наименьших квадратов (МНК-оценка), определяемая матричным равенством:

βˆ(Yn ) =(FT F)−1FTY . (6.7)

Поясним идею метода наименьших квадратов и происхождение форму-

лы (6.7). Докажем несмещенность и эффективность оценки βˆ(Yn ) в классе

линейных оценок.

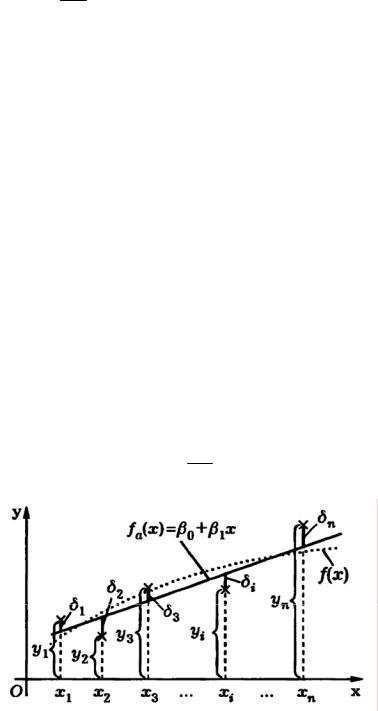
Пусть отклик Y зависит лишь от одного фактора X ( p =1 ), а искомая функция регрессии M(Y | x) = f(x) имеет график, изображенный пунктирной линией на рис. 6.4. Функция f(x) нам неизвестна, известны лишь значения отклика y1, …, yn , полученные в эксперименте при значениях факторов x1, …, xn (на рис. 6.4 точки (xi, yi ) , i =1, n , отмечены “крестиками”).

Рис. 6.4

Неизвестную функцию f(x) на основании характера расположения экспериментальных точек (они визуально расположены вдоль прямой) естественно аппроксимировать линейной функцией fa (x; β) = β0 +β1x . Отклонения