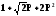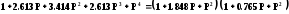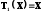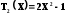2 Правила расчёта фильтров нижних частот

2.1 ОБЩИЕ ПРАВИЛА РАСЧЁТА ФИЛЬТРОВ НИЖНИХ ЧИСТОТ

;

Положив:

получим частоту среза Фазовый сдвиг на этой частоте – 450.

заменим на .

Передаточная функция фильтра:

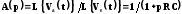
Передаточная функция определяет зависимость преобразований Лапласа выходного и входного напряжений для произвольных временных сигналов. Переход от передаточной функции к частотной характеристикидля синусоидальных входных сигналов можно выполнить, положив.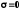

Нормированная комплексная переменная:

при

Частота среза фильтра

Тогда

при W >> 1; т.е. f >>fg

это соответствует снижению коэффициента передачи фильтра 20дБ / декаду.

Для последовательно включенных n фильтров нижних частот:

.

Где a1, a2….. an - действительные положительные коэффициенты.

при W >> 1.

Уменьшение коэффициента передачи характеризуется величиной n × 20дБ на каждую декаду. Корни передаточной функции являются отрицательными и действительными. Такими свойствами обладают пассивные RC фильтры n – ного порядка.

В общем, виде передаточная функция фильтра нижних частот:

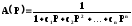(2.1.1)

где c1, c2,×××× cn – положительные действительные коэффициенты.

Порядок фильтра определяется максимальной степенью переменной Р.

Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, то в этом случае вместо этого представления следует записать в виде произведения сомножителей второго порядка.

(2.1.2)

где ai и bi – положительные действительные коэффициенты. Для нечетных порядков полинома bi = 0.

2.2 ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА

Модуль .

График функции | А* |2 должен быть по возможности горизонтальным на частотах входного сигнала, меньше частоты среза. Т.к. в этой области W < 1, необходимо, чтобы функция | А* |2 зависела только от старшей степени W.

.(2.2.1)

Коэффициент К2n определяется из условий нормировки, связанного с необходимостью обеспечения снижения коэффициента передачи фильтра на 3дБ при частоте среза W = 1.

откуда К2n = 1.

Тогда для фильтра Баттерворта n – ного порядка выражение имеет следующий вид:

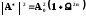(2.2.2)

Для расчета | А* | необходимо знать соответствующий выражению (2.2.2) комплексный коэффициент передачи.

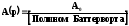
n	Полином Баттерворта
1	1 + Р
2
3
4

Аналитические выражения для коэффициентов аi и bi передаточной функции (1.1.2) для фильтра Баттерворта.

Коэффициенты ai и bi :

для четных n

bi = 1.

Для нечетных n

а1 = 1 b1 = 0

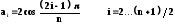
bi = 1

2.3 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА

Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она имеет волнообразный характер с постоянной амплитудой. При задании порядка фильтра более резкому спаду амплитудно-частотной характеристики соответствует большая неравномерность в полосе пропускания.

В области функцияколеблется между 0 и 1, а при Х > 1 монотонно возрастает.

N	Полиномы Чебышева
1
2
3
4

Выражение для фильтров нижних частот на основе полиномов Чебышева:

Постоянный коэффициент k выбирается так, чтобы при Х = 0 выполнялось условие , т.е. k = 1 для полиномов нечетного порядка; k= 1 +e2 для четных n. Множитель e определяет степень неравномерности характеристики фильтра..

Отсюда

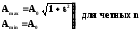
Неравномерность дБ
	0,5	1	2	3
	1,059	1,122	1,1259	1,413
К	1,122	1,259	1,585	1,935
e	0,349	0,509	0,765	0,998

Однако, удобно вычислять полюсы передаточной функции фильтра непосредственно по:

;

и используя выражение для коэффициентов Баттерворта. Объединяя комплексно сопряженные полюсы передаточной функции для коэффициентов аi и bi:

Для четных n

для нечетных n :

b/I = 0

a/I = 1/ sh g

где

подставив а/i ; b/i вместо аi и bi в выражение

получим передаточную функцию фильтра Чебышева нижних частот, в котором Р нормировано не относительно g (соответствующую коэффициенту передачи 3дБ), а относительно с – при котором коэффициент передачи в последний раз принимает значение Аmin. После заменим Р на Р, и выберем постоянную нормирования  так, чтобы коэффициент передачи P = j имел значение ; тогда, где;. Коэффициенты для аi и bi передаточных функций для фильтров до 5 порядка для значений неравномерности АЧХ равных 0,5; 1; 2; 3дБ приведены в таблице 2.3.1.

Таблица 2.3.1 Коэффициенты для расчётов ФНЧ.

N	аi	Bi		Qi
Фильтр Баттерворта
1	1,0000	0,0000	1,000	-
2	1,4142	1,0000	1,000	0,71
3	1,000	0,0000	1,000	-
	1,0000	1,0000	1,272	1,00
4	1,8478	1,0000	0,719	0,54
	0,7654	1,0000	1,390	1,31
5	1,0000	0,0000	1,000	-
	1,6180	1,0000	0,859	0,62
	0,6180	1,0000	1,448	1,62
Фильтр Чебышева с неравномерностью 1дБ
1	1,0000	0,0000	1,000	-
2	1,3022	1,5515	1,000	0,96
3	2,2156	0,0000	0,451	-
	0,5442	1,2057	1,363	2,02
4	2,5904	4,1601	0,540	0,78
	0,3039	1,1697	1,417	3,56
5	3,5711	0,0000	0,280	-
	1,1280	2,4896	0,894	1,40
	0,1872	1,0814	1,486	5,56

3. МОДЕЛИРОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ

1. ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА

Исследование ФНЧ Баттерворта проведём по схеме с рис.1.2.1

Выберем следующие параметры схемы:

R1=1.2 kOm;

R2=R3=2.5 kOm;

C1=C3=0.0078 uF;

C2=0.001 uF.

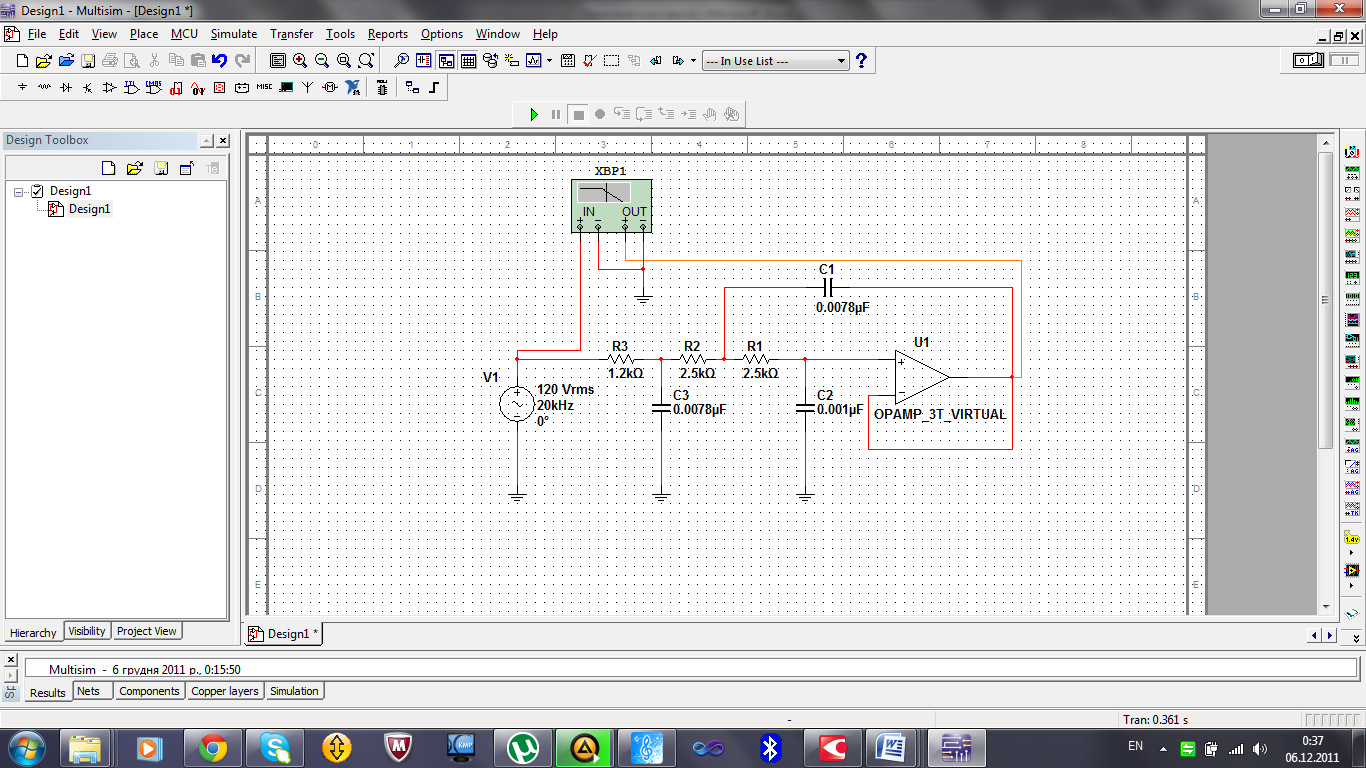
Рис.3.1.1 – Модель ФНЧ Баттерворта на ОУ

Используя блок body plotter снимем АЧХ вида:

Рис. 3.1.2 – АЧХ ФНЧ Баттерворта при f_ср=20кГц и А=1 дБ

Рис. 3.1.3 – идеальная АЧХ для ФНЧ Баттерворта

Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Баттерворта, изображенной на рисунке 3.1.3, то параметры схемы были расчитаны верно.

3.2 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА

Исследование ФНЧ Чебышева проведём по схеме 3.2.1.

Выберем следующие параметры схемы:

R1=13 kOm;

R2=11 kOm;

R3=6 kOm;

C1=0.007 uF;

C2=0.001 uF.

Рис.3.2.1 – Модель ФНЧ Чебышева

Используя блок body plotter снимем АЧХ вида:

Рис. 3.2.2 – АЧХ ФНЧ Чебышева при f_ср=20кГц и А=1 дБ

Рис. 3.2.3 – идеальная АЧХ для ФНЧ Чебышева

Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Чебышева, изображенной на рисунке 3.2.3, то параметры схемы были расчитаны верно.

ВЫВОДЫ

В результате выполнения курсового проектирования по предмету «Схемотехника аналоговых компонентов компьютерных систем» были рассмотрены следующие вопросы:

- фильтры нижних частот (ФНЧ) и их назначение;

- основные сведения об ФНЧ Баттерворта и Чебышева;

- порядок расчёта ФНЧ Баттерворта и Чебышева.

Было выполнено моделирование вышеназванных фильтров нижних частот. Как для моделирования ФНЧ Баттерворта, так и для моделирования ФНЧ Чебышева использовались схемы на операционном усилителе.

В результате моделирования были сняты амплитудно-частотные характеристики фильтров, которые близки к идеальным характеристикам, описывающим каждый из видов исследуемых фильтров.

На основании полученных результатов можно предположить, что проектирование было выполнено успешно.

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. - М.: Мир, 1982. – 512 с.

2. Справочник по активным фильтрамЖ Пер.с англ../Д.Джонсон, Дж.Джонсон, Г.Мур. – М.: Энергоатоммиздат, 1983 – 128 с.

3. Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её преминение. – М.; Салон-Р, 1999, 506 с.

4. Методические указания по курсу «Схемотехника аналоговых».Раздел «Фильтры». Для студентов заочной формы обучения. – Харьков, 2003 – 33 с.