1 Тема

1.Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с вершинами имеет рёбер и обозначается . Является регулярным графом степени .

Графы с по являются планарными. Полные графы с большим количеством вершин не являются планарными, так как содержат подграф и, следовательно, не удовлетворяют критерию Понтрягина-Куратовского.

2. Простой граф — граф, в котором нет кратных рёбер и петель

3. Дерево — это связный ациклический граф.^[1] Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.^[2]

Корневое дерево — дерево, в котором выделена одна вершина (корень дерева). Формально корневое дерево определяется как конечное множество одного или более узлов со следующими свойствами:

1. существует один корень дерева 

2. остальные узлы (за исключением корня) распределены среди непересекающихся множеств, и каждое из множеств является корневым деревом; деревья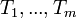называются поддеревьями данного корня

4. Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.

5. Неориентированный граф называется двудольным, если множество его вершин можно разбить на две части,,, так, что

• ни одна вершина 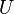в не соединена с вершинами ви

• ни одна вершина 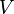в не соединена с вершинами в

Двудольный граф называется полным, если для каждой пары вершин существует ребро. Для

такой граф называется 

6. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ijравно числу рёбер из i-й вершины графа в j-ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i-й вершины.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.