Вопросы

1. Дайте определение понятия «комбинаторный анализ».

2. Что такое комбинаторная конфигурация? Приведите примеры комбинаторных конфигураций.

3. Поясните правило суммы в комбинаторном анализе.

4. Поясните правило произведения в комбинаторном анализе.

5. Что такое соединение в комбинаторном анализе?

6. Дайте определение понятиям размещения и перестановки, определите формулы их вычисления.

7. Дайте определение понятию сочетания и формулы его вычисления.

8. Как вычисляются перестановки без повторений?

9. Как вычисляются перестановки с повторениями?

10. Как вычисляются размещения без повторений?

11. Как вычисляются размещения с повторениями?

12. Как вычисляются сочетания без повторений?

13. Как вычисляются сочетания с повторениями?

14. Формула включений-исключений.

15. Урновые схемы решения комбинаторных задач. Общие положения.

Задания

1. Из состава конференции, на которой присутствует 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать?

2. В профком выбрано 9 человек. Из них надо выбрать председателя, заместителя, секретаря и культорга.

3. Из 12 слов мужского рода, 9 слов женского рода и 10 слов среднего рода надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор?

4. У одного человека есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять книгу одного на книгу другого?

5. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

6. Сколько различных слов можно получить, переставляя буквы в слове «математика», «интерпретация», «парабола».

7. В комнате 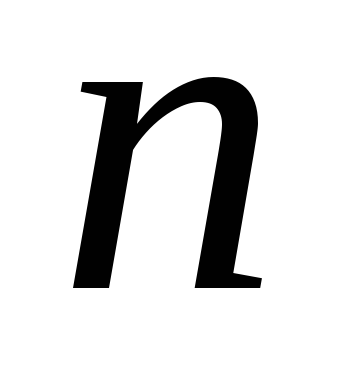лампочек. Сколько разных способов освещения комнаты, при которых горит:

а) ровно лампочек;

б) хотя бы одна лампочка.

8. A и B и еще 8 человек стоят в очереди. Сколькими способами можно расположить людей в очереди, чтобы A и B были отделены друг от друга тремя лицами?

9. В группе изучается 10 предметов. Сколькими способами можно составить расписание на понедельник, если в понедельник должно быть 4 пары и все разные?

10. Сколькими способами можно упорядочить 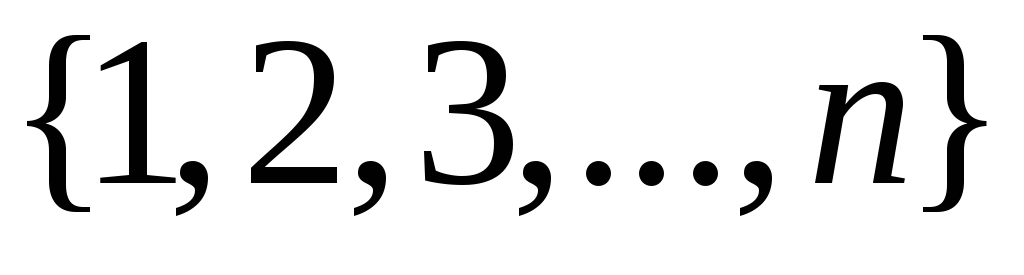чисел так, чтобы числа 1, 2, 3 стояли рядом в порядке возрастания?

11. Множество А состоит из 36 чисел, 12 из которых делятся на 6, остальные числа четные, или делятся на 3. Сколько чисел в этом множестве делится на 3, если известно, что таких чисел на 6 больше, чем четных?

12. Множество, мощностью 26, состоит из инъективных и сюръективных отображений, 14 из которых – биективные. Сколько в этом множестве сюръективных отображений, если известно, что их на 2 больше, чем инъективных?