Числа Белла

Число Белла равно количеству разбиений множества из элементов на произвольное количество непустых подмножеств, которые не пересекаются. Очевидно, что, так как существует только одно разбиение пустого множества. Например,, так как существует 5 возможных разбиений множестваиз трех элементов:

Заметим, что элементов можно разбить намножеств. При этом количество разбиений– элементного множества наподмножеств равно числу Стирлинга 2 рода. Откуда получаем формулу:

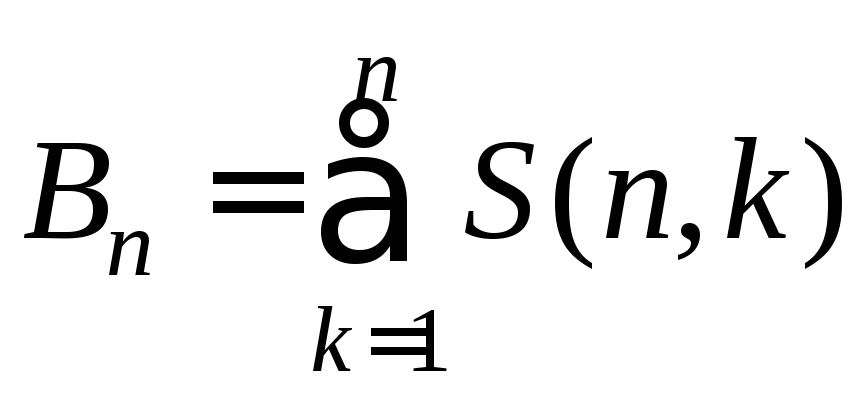
	0	1	2	3	4	5	6	7	8	9	10
	1	1	2	5	15	52	203	877	4140	21147	115975

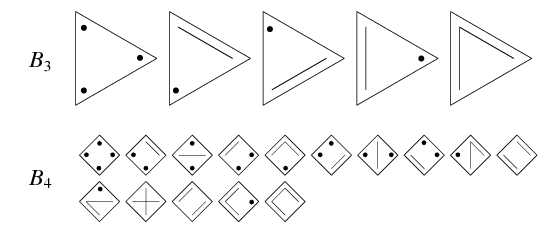
Рассмотрим следующие конструкции, в которых точки обозначают одноэлементные множества, а сегменты объединяют элементы, принадлежащие одному множеству. Из элементов можно построитьразных таких конструкций.

Теорема. Числа Белла удовлетворяют следующему рекуррентному соотношению:

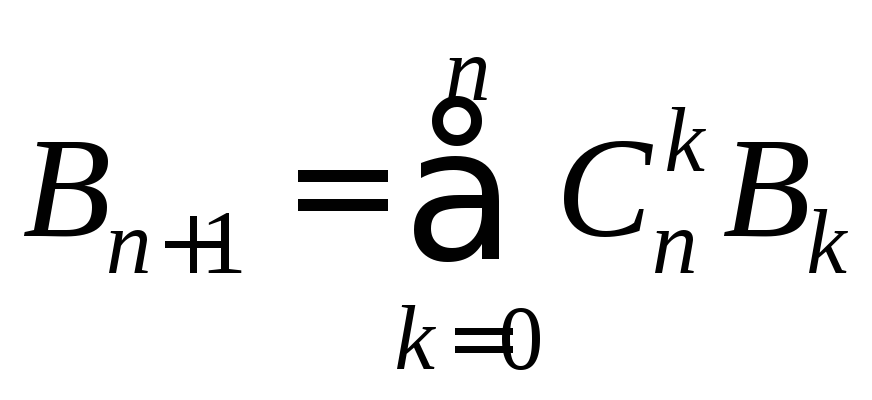
Доказательство. Рассмотрим разбиение элемента в зависимости от величины блока, в котором находится– ый элемнент. Пусть размер этого блока равен. Тогда существуетспособов выбрать в него кроме– ого ешеэлемент. Остальныеэлементов можно разбитьспособами.Таким образом:

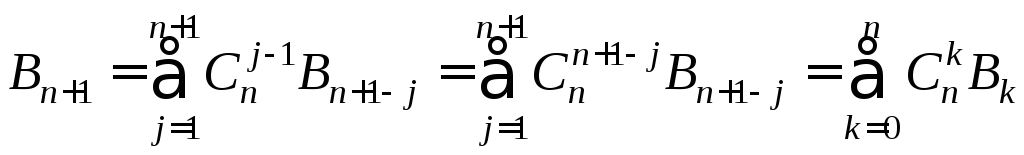
Пример.Например, . Числа Белла удовлетворяют следующему свойству:

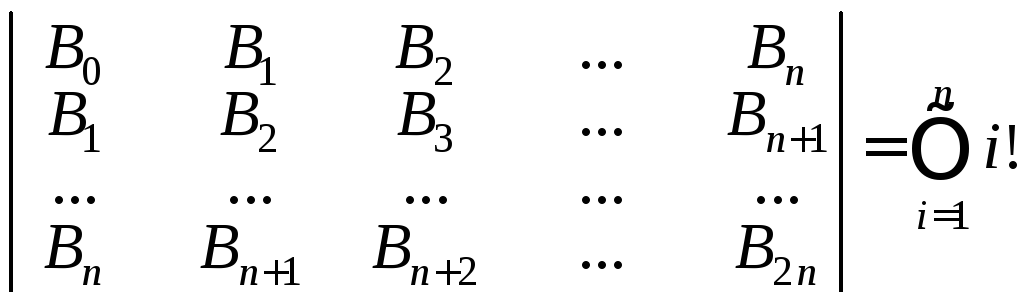
Для значений получим следующие значения детерминанта:

1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000, 6658606584104736522240000000, …

При разложении функции в ряд Маклорена коэффициенты ряда образуют числа Белла:

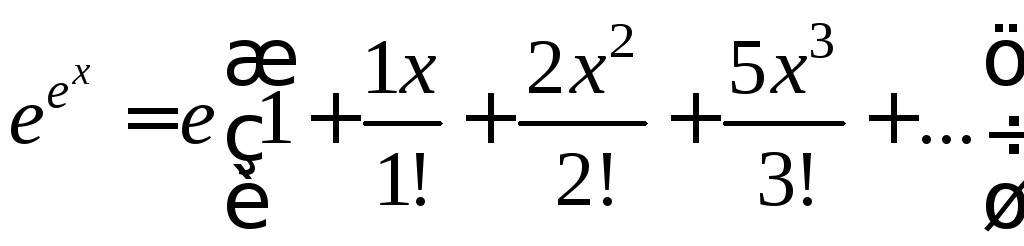
Числа могут быть построены при помощитреугольника Белла. Первая строка содержит 1. Каждая следующая строка начинается числом, стоящим в конце предыдущей строки. Каждое следующее число в строке равно сумме чиел, стоящих слева и сверху от него. Числа Белла образуют последние числа в строках.

Композиции

При решении задач про распределениеодинаковых предметов междунепустыми урнами можно говорить о разложении числав сумму натуральных слагаемых:

, где(5.18)

Два таких разложения числа считаются разными, если они отличаются хотя бы одним слагаемым. В таком случае говорят о композиции числа. В ином случае,композиция числа –это его разложение в виде (5.18), где учитываются как величины слагаемых (частей) , так и порядок их расположения в сумме.

Пример. Выписать все композиции числа 3.

3=3, 3=2+1, 3=1+2, 3=1+1+1.

Композиции с ограничениями на количество слагаемых

Число композиций числаизслагаемых равно числу распределенийодинаковых предметов поразным урнам при условии отсутствия пустых урн. Число предметов, которые попали в урну с номером, дает слагаемое . Отсюда выплывает, что.

Число всех композиций числа

(5.19)

Комбинаторика разбиений

При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой игры карты раскладываются на 3 кучки (по числу играющих) и 2 карты кладутся в “прикуп“. Играют 32 картами, т. е. каждый игрок получает по 10 карт.

Определим количество вариантов расклада при игре в преферанс:

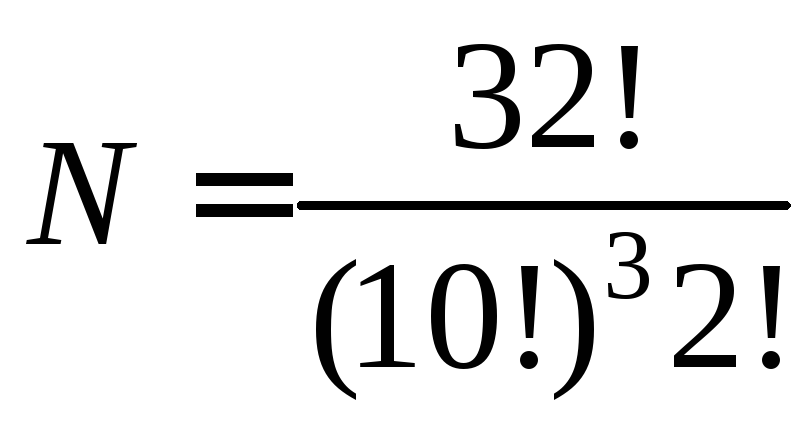
Для обоснования полученной формулы расставим все карты подряд и переставим их 32! способами. При каждой перестановке будем выделять первые 10 карт первому игроку, вторую десятку – второму, третью – третьему, а последние 2 карты будем откладывать в “прикуп”. После этого заметим, что перестановка 10 карт в руках каждого игрока не меняет варианта расклада, как и положения 2 карт в прикупе. Поэтому 32! разделим три раза на 10! и еще на 2!

В общем случае, если раскладываются разных предметов поящикам так, чтобы в 1-й ящик (кучку, игроку в руки) попалопредметов, во второй предмета, в-й –предметов, при этом, то число вариантов расклада

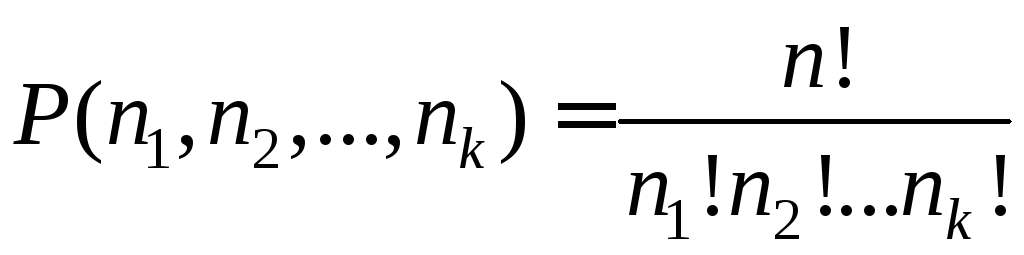(5.20)