Частный случай теоремы о включениях и исключениях

В некоторых случаях количество объектов, обладающих определенным набором свойств, зависит только от числа этих свойств. Тогда формула для подсчета числа объектов, не обладающих ни одним из выделенных свойств, упрощается.

При произвольном имеем:

(5.8)

В общем случае при перестановке предметов количество расстановок, при которых ни один предмет не находится на своем месте:

(5.9)

Полученное значение иногда называютформулой полного беспорядкаилисубфакториалом. Субфакториал можно представить и так:

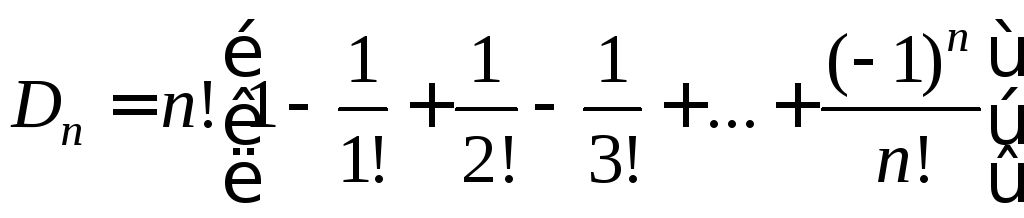, (5.10)

где выражение в [...] стремится к при неограниченном возрастании.

Субфакториал имеет свойства, похожие на свойства обычного факториала. Например,

– для обычного факториала,

– для субфакториала.

Субфакториалы легко вычисляются по формуле

(5.11)

Некоторые начальные значения субфакториалов:

	1	2	3	4	5	6	7	8	9
	0	1	2	9	44	255	1784	14273	128456

Задачи о распределении предметов по урнам (урновые схемы решения комбинаторных задач) Задачи о размещении предметов

Решая задачи размещения (распределения предметов по урнам) необходимо определить, являются ли предметы одинаковыми или различными, учитывать порядок или нет, различаются ли урны между собой.

Если невозможно однозначно что-либо определить, то необходимо сделать предположение.

Распределение n разных предметов по k урнам

Количество размещений по k урнам n разных предметов при условии, что в первую урну попало предметов, во вторую –в последнюю –предметов. равно:

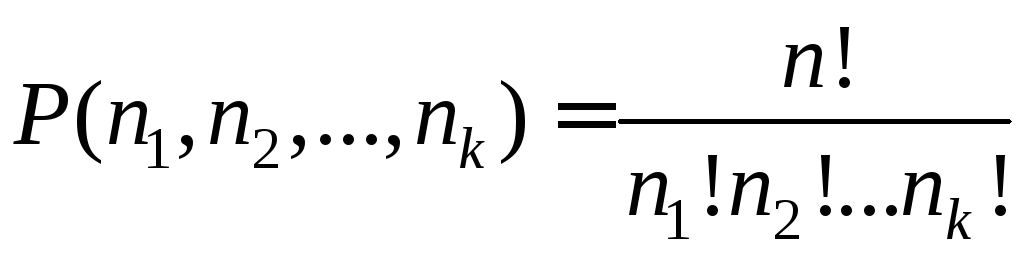(5.12)

Распределение n одинаковых предметов по k урнам

Установим, что n одинаковых предметов между k урнами можно разделить способами:

(5.13)

Количество искомых распределений n одинаковых предметов между урнами равняется количеству перестановок изпредметов с повторениямипредметов первого типа ипредметов второго типа, т.е. равно.

Если делить справедливо, с уровнем справедливости , то каждый участок распределения должен получать минимумпредметов. Тогда сначала раздадим каждому попредметов. После чего остаетсяпредметов, которые и распределим по усмотрению. Это можно сделать способами

(5.14)

Распределение разных предметов без учета порядка предметов по урнам

Нужно разделить n разных предметов по урнам, емкость которых не ограничена. Первый предмет можно положить в любую изурн, второй(независимо от первого), тоже вурн и т.д. По правилу произведения предметы можно разделитьспособами.

Распределение разных предметов с учетом их порядка в урнах

Если не ограничивать количество предметов в урнах и если предметы не разнятся между собой, то количество таких распределений равно

Каждому способу разделения одинаковых предметов между урнами соответствует способов распределения разных предметов с учетом их порядка, которые получаются с помощью перестановок предметов между собой без изменения количества предметов в урнах. По правилу умножения получаем искомое количество распределений:

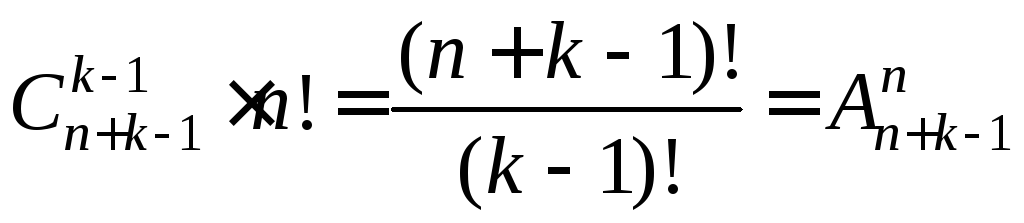(5.15)

Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты

Обозначимколичество способов разделения n разных предметов междуодинаковыми урнами так, чтобы каждая урна была не пустой. Из каждого такого распределения можно получитьаналоговых распределений по разным урнам. Таким образом, количествораспределенийразных предметов междуразными урнами с использованием каждой урны в каждом распределении (не пустых урн) равно(5.15)

Числа Моргана

Числоносят название чисел Моргана.

Формула

(5.16)

выплывает из формулы включений и исключений.

Числа Стирлинга

Числа Стирлинга – комбинаторные понятия, введенные Джеймс‎ом Стирлингом в середине XVIII века.

Числа называются числами Стирлинга второго рода.

Числам Стирлинга удовлетворяет рекурсивное соотношение:

(5.17)

Число Стирлинга первого рода равно количеству способов представленияобъектов в видециклов и обозначается(читается “циклов из”).

Например, циклы из 4 элементов иявляются одинаковыми. Цикл можно прокручивать, так как его конец соединен с началом.

Пример. Например, существует 11 различных способов составить два цикла из четырех элементов:

Поэтому .

Единичный цикл (цикл, состоящий из одного элемента) – это то же самое, что и единичное множество. 2-цикл подобен 2-множеству, поскольку как и. Однако уже существует два различных 3-цикла:и. Из любого-элементного множества могут быть составленыциклов, если(всего имеетсяперестановок, а каждый цикл соответствует сразуиз них, так как отсчет цикла может быть начат с любого из его элементов). Поэтому

Если все циклы являются единичными или двойными, то Например,

Выведем рекуррентную формулу для вычисления чисел Стирлинга первого рода. Каждое представление объектов в видециклов либо помещает последний объект в отдельный циклспособами, либо вставляет этот объект в одно изциклических представлений первыхобъектов. В последнем случае существуетразличных способов подобной вставки. Например, при вставке элементав циклможно получить только 3 разных цикла:. Таким образом, рекуррентность имеет вид:

0	1
1	0	1
2	0	1	1
3	0	2	3	1
4	0	6	11	6	1
5	0	24	50	35	10	1
6	0	120	274	225	85	15	1
7	0	720	1764	1624	735	175	21	1
8	0	5040	13068	13132	6769	1960	322	28	1
9	0	40320	109584	118124	67284	22449	4536	546	36	1

Треугольник Стирлинга для числа циклов

Теорема. Имеет место соотношение:

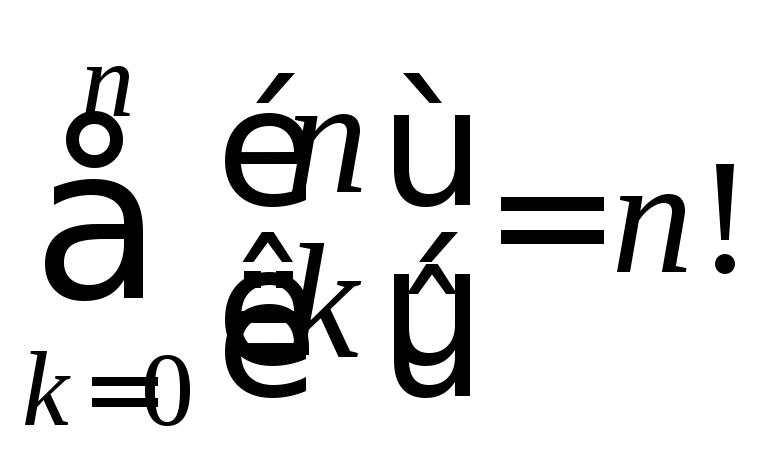
Доказательство. обозначает число перестановокобъектов, которое содержит ровноциклов. Если просуммировать по всем, то должно получиться общее число перестановок, равное.

Число Стирлинга второго рода равно количеству способов разбиения множества изэлементов нанепустых подмножеств и обозначается(читается “подмножеств из”).

Пример. Например, существует 7 способов разбиения четырехэлементного множества на две части:

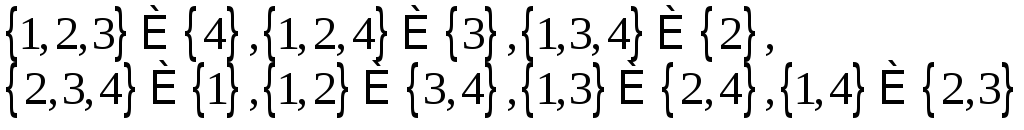
Поэтому .

Рассмотрим значения чисел Стирлинга для малых значений :

1. . Существует только один способ разбиения пустого множества на нулевое число непустых частей, поэтому. Для непустого множества нужна по крайней мере хотя бы одна часть, так чтопри.

2. . Существует только один способ помещенияn элементов в одно-единственное непустое множество, поэтому при. Однако, так как 0-элементное множество пусто.

3. . Очевидно, что. Если множество изобъектов разделено на две непустые части, то одна из этих частей содержит последний объект и некоторое подмножество изобъектов. Имеетсяподмножеств изобъектов. Поскольку все объекты нельзя поместить в одну часть, то.

0	1
1	0	1
2	0	1	1
3	0	1	3	1
4	0	1	7	6	1
5	0	1	15	25	10	1
6	0	1	31	90	65	15	1
7	0	1	63	301	350	140	21	1
8	0	1	127	966	1701	1050	266	28	1
9	0	1	255	3025	7770	6951	2646	462	36	1

Треугольник Стирлинга для числа подмножеств

Выведем рекуррентное соотношение, при помощи которого можно будет вычислить значения . Если задано множество изобъектов, которое должно быть разбито наk непустых частей, то мы либо помещаем последний объект в отдельный класс, а оставшиеся объект разбиваем начастьспособами, либо помещаем его в любую изчастей, на которые разбитыобъект. В последнем случае имеетсявозможных вариантов, поскольку каждый изспособов распределения первыхобъектов понепустым частям даетk подмножеств, с которыми можно объединить объект. Имеем рекуррентную формулу: