
- •Элементы комбинаторного анализа
- •Общие определения комбинаторики
- •Понятие -выборки
- •Модели комбинаторных конфигураций
- •Общие правила и задачи комбинаторики
- •Основные правила комбинаторики
- •Размещения без повторений
- •Размещения с повторениями
- •Перестановки без повторений
- •Перестановки с повторениями
- •Сочетания без повторений
- •Сочетания с повторениями
- •Теорема и формула включений и исключений
- •Решето Эратосфена
- •Частный случай теоремы о включениях и исключениях
- •Задачи о распределении предметов по урнам (урновые схемы решения комбинаторных задач) Задачи о размещении предметов
- •Распределение n разных предметов по k урнам
- •Распределение n одинаковых предметов по k урнам
- •Распределение разных предметов без учета порядка предметов по урнам
- •Числа Белла
- •Композиции
- •Композиции с ограничениями на количество слагаемых
- •Комбинаторика разбиений
- •Подходы к изучению комбинаторных объектов и чисел Понятие продуктивной функции
- •Рекуррентные соотношения в комбинаторике
- •1. Задача о наклейке марок.
- •Практика Примеры решения типовых задач
- •Вопросы
- •Задания
Элементы комбинаторного анализа
Теория
Общие определения комбинаторики
Понятие -выборки
Определение.Пусть заданоrмножеств:![]() ,
при этом
,
при этом![]() ,
тогдаr-выборкойназывается
упорядоченная совокупность элементов
вида:
,
тогдаr-выборкойназывается
упорядоченная совокупность элементов
вида:
![]() (5.1)
(5.1)
Определение.Множество всех выборок![]() называетсятеоретико-множественным произведениемили произведением r множеств
называетсятеоретико-множественным произведениемили произведением r множеств![]() .
Обозначается
.
Обозначается![]()
!!!
![]() -выборка
не множество, а элемент теоретико-множественного
произведения.
-выборка
не множество, а элемент теоретико-множественного
произведения.
В
![]() -выборке
каждый элемент(компонента) может
повторяться, но их порядок фиксирован.
-выборке
каждый элемент(компонента) может
повторяться, но их порядок фиксирован.
Определение.Две упорядоченные выборкиравныилиэквивалентнытогда и только тогда, когда соответствующие элементы равны
![]()
Определение.r-выборка с
произвольным порядком размещения
компонент называетсянеупорядоченной
r-выборкой. Обозначается![]()
Модели комбинаторных конфигураций
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
Определение.Размещением
![]() из
из![]() элементов по
элементов по![]() называетсяупорядоченный
набориз
называетсяупорядоченный
набориз![]() различных элементов некоторого
различных элементов некоторого![]() -элементного
множества.
-элементного
множества.
Определение.Перестановкой![]() из
из![]() элементов (например, чисел
элементов (например, чисел![]() )
называется всякий упорядоченный набор
из этих элементов. Перестановка также
является размещением из
)
называется всякий упорядоченный набор
из этих элементов. Перестановка также
является размещением из![]() элементов
по
элементов
по![]() .
.
Определение.Сочетанием![]() из
из![]() по
по![]() называется набор
называется набор![]() элементов, выбранных из данных
элементов, выбранных из данных![]() элементов. Наборы, отличающиеся только
порядком следования элементов (но не
составом), считаютсяодинаковыми,
этим сочетания отличаются от размещений.
элементов. Наборы, отличающиеся только
порядком следования элементов (но не
составом), считаютсяодинаковыми,
этим сочетания отличаются от размещений.
Определение.Композицией
числа![]() называется всякое представление
называется всякое представление![]() в виде упорядоченной суммы целых
положительных чисел.
в виде упорядоченной суммы целых
положительных чисел.
Определение.Разбиением
числа![]() называется всякое представление
называется всякое представление![]() в виде неупорядоченной суммы целых
положительных чисел.
в виде неупорядоченной суммы целых
положительных чисел.
Общие правила и задачи комбинаторики
Основными и типичными операциями и связанными с ними задачамикомбинаторики являются:
1) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, –
составление перестановок;
2) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, – составление сочетаний;
3) образование упорядоченных подмножеств – составление размещений.
Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.
Основные правила комбинаторики
Правила суммы и произведения используются при вычислении количества различных комбинаций.
Правило
суммы. Если
![]() и
и![]() – несвязанные события, и существует
– несвязанные события, и существует![]() возможных исходов события
возможных исходов события![]() ,
и
,
и![]() возможных исходов события
возможных исходов события![]() ,
то возможное число исходов события «
,
то возможное число исходов события «![]() или
или![]() »
равно сумме
»
равно сумме![]() .
.
Интерпретация. Если элемент
![]() можно выбрать
можно выбрать![]() способами, а элемент
способами, а элемент![]() –
–![]() способами, то выбор элемента
способами, то выбор элемента![]() можно осуществить
можно осуществить![]() способами. Пусть
способами. Пусть![]() – попарно непересекающиеся
множества,
– попарно непересекающиеся
множества,
![]() ,
где
,
где![]() .
Тогда, очевидно, выполняется равенство
.
Тогда, очевидно, выполняется равенство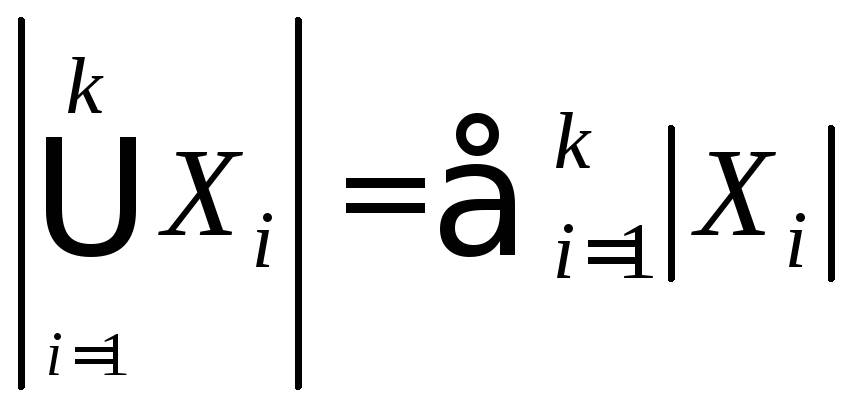 .
.
Правило произведения.
Если дана последовательность
![]() событий с
событий с![]() возможными исходами первого,
возможными исходами первого,![]() – второго, и т.д., вплоть до
– второго, и т.д., вплоть до![]() возможных исходов последнего, то общее
число исходов последовательности k
событий равно произведению
возможных исходов последнего, то общее
число исходов последовательности k
событий равно произведению![]() .
.
Правило произведения тоже
можно сформулировать на языке теории
множеств. Пусть
![]() обозначает множество
обозначает множество![]() исходов первого события,
исходов первого события,![]() – множество
– множество![]() исходов второго, и т. д. Тогда любую
последовательность
исходов второго, и т. д. Тогда любую
последовательность![]() событий можно рассматривать как элемент
декартова произведения
событий можно рассматривать как элемент
декартова произведения![]() ,
чья мощность равна
,
чья мощность равна![]() .
.
Пример. Из 28 костей домино берутся 2 кости. В каком числе комбинаций вторая кость будет приложима к первой?
На первом шаге имеется два варианта: выбрать дубль (7 комбинаций) или не дубль (21 комбинация). В первом случае имеется 6 вариантов продолжения, во втором – 12.
Общее число благоприятных
комбинаций равно:
![]() .
.
А всего вариантов выбора 2 костей из 28 равно 378; т. е. при большом числе экспериментов в 7 случаях из 9 (294/378 = 7/9) при выборе 2 костей одна кость окажется приложимой к другой.
