ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Навчально-консультаційний центр

У м. Кривому Розі

Кафедра вищої математики

ВИЩА МАТЕМАТИКА

Приклад виконання контрольної роботи №1

ХАРКІВ

2009 р.

Завдання №1

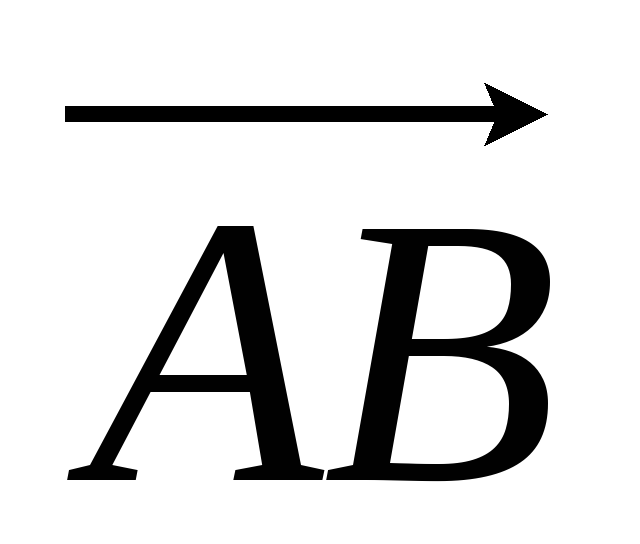
Задані координати чотирьох вершин піраміди ABCD: А(-2,0,0), В(1,1,-1), С (-1,3,0),

D(-1,0,2).

Необхідно обчислити:

1. довжину ;

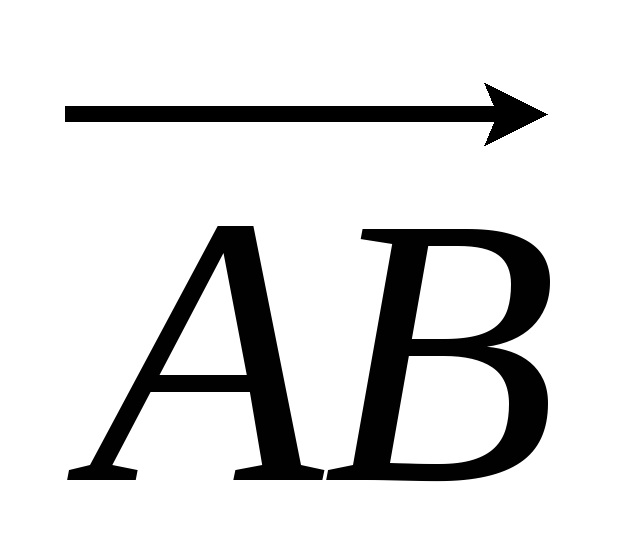2. кут між векторами ;

3. площу трикутника ;

4. об'єм піраміди;

5. довжину висоти DH піраміди, проведеної до площини грані ABC.

Необхідно скласти рівняння:

6. прямої АВ;

7. площини АВС;

8. висоти піраміди DH, проведеної з D перпендикулярно к площі АВС;

9. медіани АМ трикутника АВС;

10. висоти АК трикутника АВС;

11. бісектриси AL трикутника АВС.

1. Вектор має координати: (3,1,-1). Тому його довжина дорівнює: (од).

2. Кут між векторами та визначається по формулі .

Обчислимо довжину вектора (од).

Скалярний добуток обчислювався по формулі

3. Площа трикутника АВС

. Обчислимо координати векторів та та векторний добуток *.

(од)

4. Об'єм піраміди ABCD

5. Довжину висоти DH піраміди обчислимо з формули

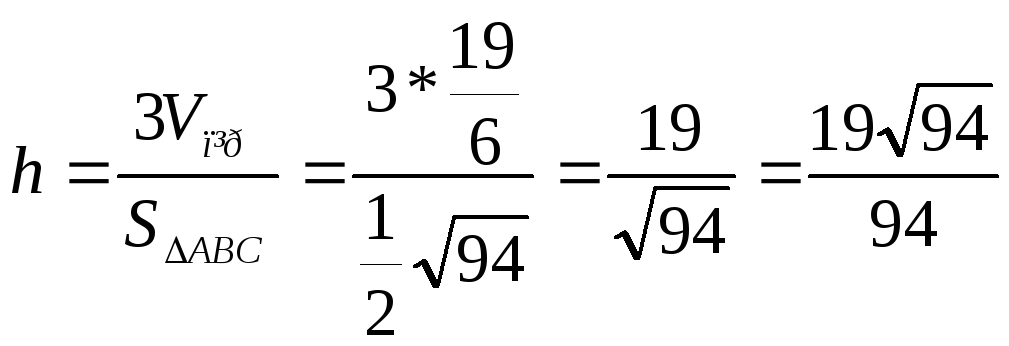(од).

6. Рівняння прямої АВ має вигляд , т.я. задані дві точки цієї прямої А та В.

Підставляє в останнє рівняння координати точок А та В, отримаємо

7. Рівняння площини АВС запишемо у вигляді 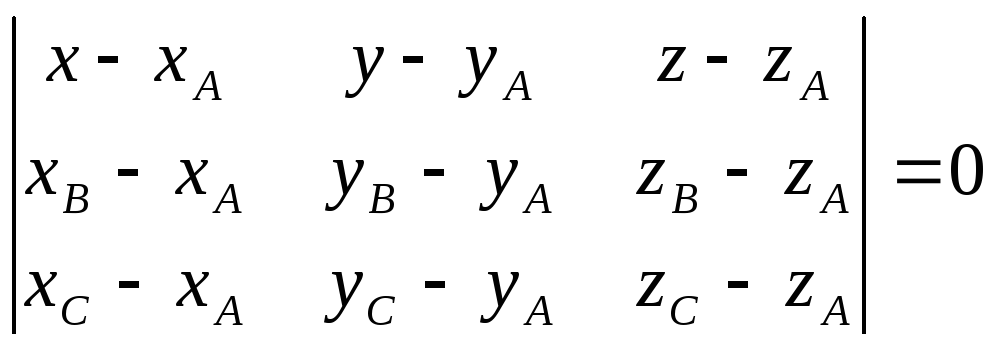, т.я. задані координати трьох точок А,В,С.

Рівняння площини АВС: 3x-y-8z+6=0

8. Рівняння висоти піраміди DH

Координати точки D відомий, а напрямний вектор прямої колінеарний вектору нормалі до площини АВС. Вектор нормалі до площини АВС має координати . Тому рівняння прямої DH має вигляд

9. Рівняння медіани АМ має вид .

Точка М-середина відрізку ВС має координати

Таким чином, рівняння медіани АМ має вигляд

10.Рівняння висоти АК

Напрямний вектор прямої , вектор перпендикулярний вектору - нормалі до площини АВС та вектору . Тому вектор може бути обчислений за формулою:

Рівняння висоти АК має вигляд

11.Точка L-точка перетину бісектриси AL зі стороною ВС ділі відрізок ВС на частини, довжина яких пропорційна довжинам прилягаючих сторін, тобто

Таким чином та

По формулам ділення відрізку в даному відношені знаходимо координати точки L

;

Рівняння бісектриси AL

Підставляючи в останнє рівняння координати точок A та L, отримаємо

Завдання №2

Скласти рівняння площини, яка проходе через точку та пряму

Р

L

Рівняння іскомої площини , де координати точки , розміщеної на прямій L та належить площині Р.

Вектор нормалі до площини Р визначаємо з умови , де .

Таким чином та управління площиною має вигляд

Завдання №3

Обчислити значення многочлена від матриці А, якщо ,

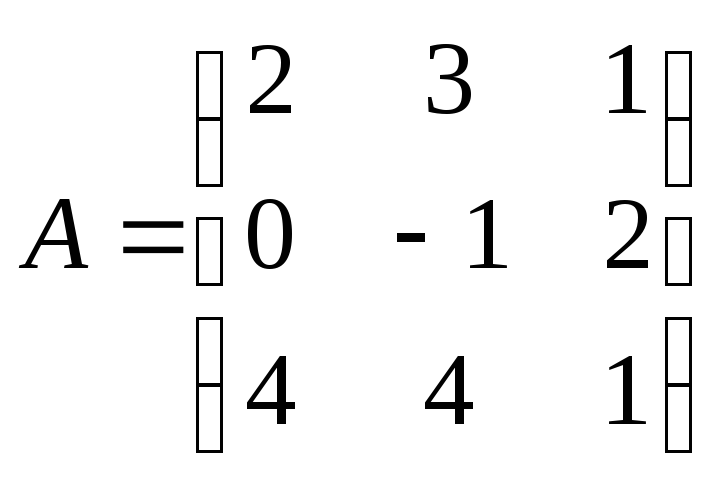
Завдання №4

Знайти межі:

1)

Відповідь:

2)

Відповідь:

3)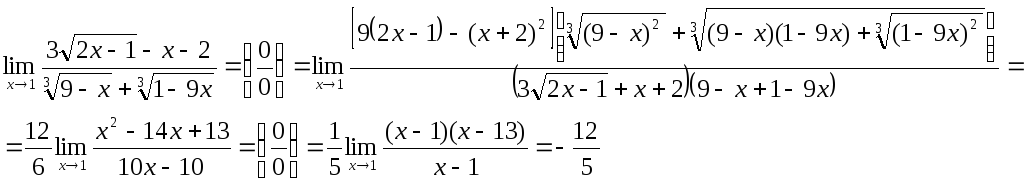Відповідь:

4) , позначимо , тоді

Завдання №5

Знайти похідну даної функції та її значення при х=а

Відповідь:

Завдання №6

Знайти похідну . Так як , то дифференцируя, отримаємо:

або

Відповідь:

Завдання №7

Знайти рівняння дотичної до кривої до точки М(1,2). Рівняння дотичної , де

Знайдемо значення t відповідне точці М: при х=1, маємо тобто .

, таким чином

Відповідь:

Завдання №8

Знайти межі по правилу Лопіталя:

1)

Відповідь:

2) , маємо невизначеність, нехай , тоді

Отже

Відповідь:1

Завдання №9

Досліджувати функцію і побудувати її графік

Дослідження функції без похідної

1. Перебування області визначення

2. Перебування точок перетинання графіка з осями Х и У

3. Дослідження функції на парність і непарність

Якщо функція парна = > f (-x) = f (x)

Якщо функція непарна = > f (-x) = - f (x)

Якщо функція парна, то її графік симетричний щодо осі ОУ, тому досить побудувати тільки частину функції при х > 0, а потім симетрично відбити.

Якщо функція непарна, то вона симетрична відносно початку координат, досить побудовати графік при х > 0, а потім повернути графік на 180 градусів.

4. Досліджувати функцію на періодичність

то - період функції

Всі алгебраїчні функції не періодичні.

5. Перебування асимптот кривих.

а). х = а (вертикальна)

б).

(невертикальна)

в). у = А(горизонтальна)

ІІ. Дослідження функції за допомогою першої похідної

- не існує

1. Перебування проміжків монотонності функції.

2. Дослідження функції на екстремум.

Дослідження за допомогою другої похідної

- не існує

1. Перебування проміжків збереження кривизни функції

2. Перебування крапок перегину

ІV. Побудова графіка функції спираючи на отриману інформацію

І. Дослідження функції без похідної

1.

2. графік з віссю ОХ не перетинається тому що

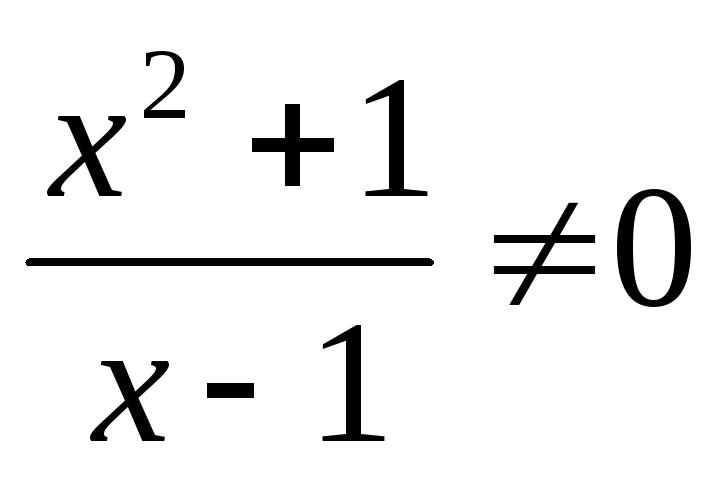
х=0 т М(0;-1)- перетинання графіка з віссю ОУ

3. Функція ні парна, не парна (індиферентна)

4. Функція не є періодичною

5. а). Вертикальна

тобто. х=1 - вертикальна асимптота

б). Горизонтальна

тобто горизонтальних асимптот немає

в). Похила

у=х+1 – похила асимптота

ІІ. Дослідження функції за допомогою першої похідної

1.

метод інтервалів

+ +

-0,42 - 2,42

- функція зростає

тобто (дивитися перегин)

- функція убуває

у

у= х + 1

0 1

-0,42 2,42 х



2. Дослідження функції на екстремум.

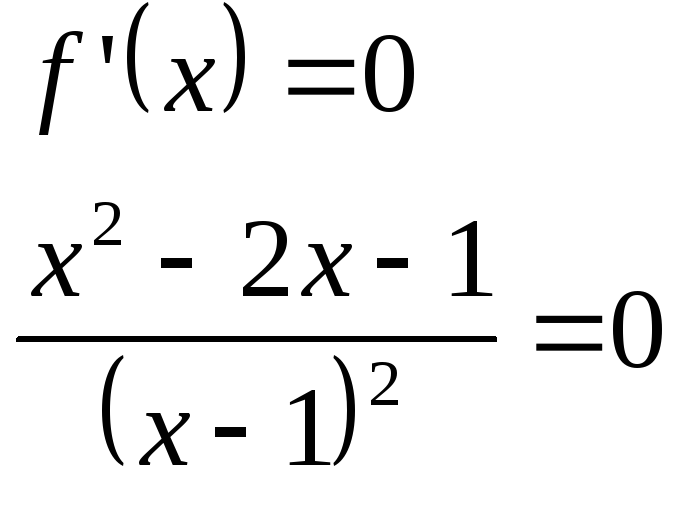
- стаціонарні крапки

скористаємося достатньою умовою

X	-1	-0.42		0
F’(x)	+	0		-
f(x)		max		
	-0.82

X	2	2.42		3
f’(x)	-	0		+
f(x)		min		
	4.7

ІІІ. Дослідження за допомогою другої похідної

1. Перебування проміжків збереження кривизни функції

- функція увігнута

2. Перебування точок перегину. Функція не має точок перегину так як

ІV. Побудова графіка функції спираючи на отриману інформацію

у

4,7

1

-0,42 0

1 2,42 х

-1



_

9