Matan_theory

1. Границя послідовності. Означення. Геометричний зміст. Число а називається границею послідовності {x_n}, якщо для будь-якого е>0 знайдеться такий N(), що для всіх n>N() виконується нерівність |x_n-a|<. Геометрично: x_n<a+; x_n>a- таким чином x_nO(a, ). (нарисовать этот окіл на оси координат)

2. Границя функції в точці. Означення. Геометричний зміст.

y=f(x) визначена в точках околу за виключенням цієї точки. Число А називається границею функції y=f(x) в точці x=a, якщо для будь-якого >0 знайдеться таке >0, що для всіх x, які задовольняють умову 0<|x-a|< , виконується нерівність |f(x)-A|<.

Число А називається границею функції y=f(x) в точці x=a, якщо для будь-якого >0 знайдеться таке >0, що для всіх x, що належать О(a, ), x≠ a відповідні значення f(x) належать О(A, ). (нарисовать координаты х,у, изобразить функцию, два соответствующие промежутка на х и у)

3. Неперервність функції в точці. Означення.

Будемо вважати, що функція y=f(x) визначена у всіх точках О(a,r) і у самій т. х=а. Функція f(x) неперервна в т. х=а, якщо , або якщо .

4. Точки розриву функції. Їх класифікація. Приклади.

Точки, в яких порушуються умови неперервності функцій, називаються точками розриву.

Точки розриву I роду двох типів: точки усувного розриву та точки розриву типу «стрибок».

Для точок розриву I роду: ∃ f(a+0), f(a-0).

а) усувний розрив: f(a+0)=f(a-0)≠ f(a);

б) розрив типу «стрибок»: f(a+0) ≠f(a-0).

Для точок розриву II роду: хоча б одне з значень f a( + 0) чи f a( − 0) нескінченне або

не існує.

5. Перша важлива границя. Її наслідки.

– перша важлива границя.

Наслідки: ; ; .

6. Друга важлива границя. Її наслідки.

– друга важлива границя.

Наслідки: ; ; .

7. Порівняння нескінченно малих.

Нехай функції α(x) і β(x) нескінченно малі при x→a .

Якщо , то α ( x) називається нескінченно малою вищого порядку малості, ніж β(x).

Коротко: α(x)=o(β(x)) , x→a (o – мале від β ( x) ), по іншому α(x)<< β(x) – α(x)значно менше, ніж β ( x).

8. Властивості еквівалентних нескінченно малих.

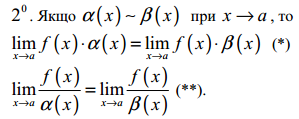
9. Ланцюжок еквівалентних нескінченно малих.

10. Еквівалентні нескінченно великі функції. Приклади.

Нехай функції f (х) і φ(x) нескінченно великі при x→а . Для цих функцій поняття еквівалентних вводиться так само, як і для нескінченно малих.

11. Похідна. Означення. Геометричний зміст. Односторонні та нескінченно великі похідні.

Для заданої функції y=f(x), знайдемо приріст △y , задавши приріст аргументу △x в

точці x . △y=f(x+△x)-f(x)

Якщо існує границя , то ця границя називається похідною від функції f(x) в точці x і позначається: y′, dy/dx.

y′ = tg(α) – кутовий коефіцієнт дотичної, проведеної до графіка функції y=f(x) в точці A(x,f(x)).

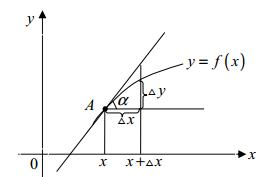
Якщо , то кажуть, що в точці x існує нескінченна похідна.

12. Теорема про зв'язок між існуванням скінченної похідної в точці і неперервністю функції в точці.

Якщо функція y= f(x) має скінченну похідну в т. x , то вона неперервна в цій точці.

13. Диференціювання обернених функцій.

Т.1.Якщо функція y=f(x) неперервна та зростаюча (спадна) на відрізку [a,b], то існує обернена функція y= φ(x), неперевна та зростаюча (спадна) на відрізку[c,d], c= φ(a), d= φ(b).

Т.2. Якщо для функції y=f(x) існує обернена функція y= φ(x), то або .

14. Диференціювання складної показникової функції.

Складною показниковою функцією називається функція вигляду y=u(x)^v(x), де u(x)>0.

15. Диференціал функції. Означення. Правила обчислення. Геометричний зміст.

Диференціалом функції y=f(x) в т. x називається вираз вигляду

Правила обчислення:

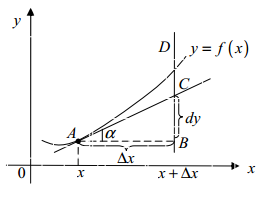BC=dy, BD=Δy.

16. Гіперболічні функції. Означення. Диференціювання.

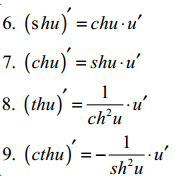
17. Похідні вищих порядків та правила їх знаходження.

Нехай y=f(x). Тоді – похідна є функцією від x .

Похідна від похідної першого порядку – це друга похідна. .

18. Теорема Коші та теорема Лагранжа про диференційовані функції.

Теорема Коші: якщо функції f(x) та g(x) задовольняють умови:

1) неперервні на відрізку [a,b],

2) диференційовні на інтервалі (a,b),

3) g′(x) ≠ 0 на інтервалі (a,b),

то існує така точка c ∈(a,b), що виконується рівність: .

Теорема Лагранжа : якщо функція f(х) задовольняє умови:

1) неперервна на відрізку [a,b],

2) диференційовна на інтервалі (a,b),

то існує така точка c ∈(a,b), що виконується рівність: .

19. Теорема Тейлора та Маклорена. Розкладання функцій за формулою Маклорена (у = е^х, y = sin x).

Розкладання у = е^х, y = sin x за формулою Маклорена:

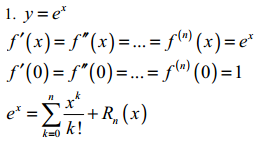
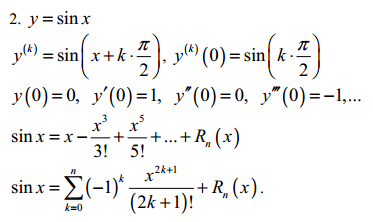
20. Екстремуми функцій. Необхідні та достатні умови.

Необхідна умова екстремуму: якщо функція f (х) диференційовна в т. х₀ і досягає в цій точці локального екстремуму, то .

Точки, в яких , називаються стаціонарними.

Точки, в яких ∞ або не існує називаються критичними точками I роду.

Достатня умова екстремуму: нехай х₀ – критична точка функції f (x) .

Якщо при переході через цю точку зліва направо f ′(x) змінює знак з «+» на «–», то в точці x= х₀ функція досягає максимуму; якщо ж f ′(x) змінює знак з «–» на «+», то в точці x= х₀ функція досягає мінімуму.

21. Невизначений інтеграл. Означення. Властивості.

Невизначеним інтегралом від функції f (x) на проміжку (a,b) називається сукупність первісних F(x) + C для функції f (x) на цьому проміжку, де С – довільна стала, а функція F(x) така, що F′(x) = f(x).

Властивості:

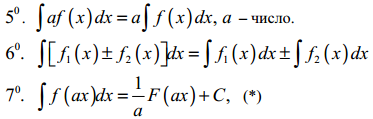
22. Метод заміни змінної в невизначеному інтегралі. Метод підведення під знак диференціала.

Нехай

а) функція f (х) неперервна на (a,b);

б) функція x = (t) неперервна і диференційовна на (c,d);

в) функція x = (t) має обернену функцію t= ϕ(x), яка є диференційовною.

Тоді має місце формула: .

Метод підведення під знак диференціала є частинним випадком методу заміни змінної і базується на властивості інваріантності (незмінності) формули інтегрування відносно змінної інтегрування.

.

23. Інтегрування частинами в невизначеному інтегралі. Класи функцій, що інтегруються частинами.

Нехай функція u=u(x) та v=v(x) диференційовні, тоді має місце формула:

Класи функцій, що інтегруються частинами:

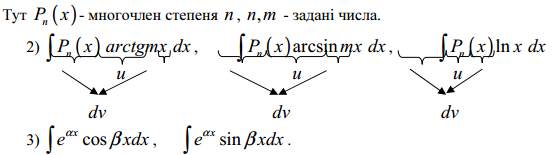
24. Інтегрування раціональних дробів. (Перших трьох типів найпростіших дробів з доведенням).

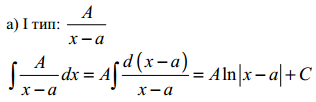
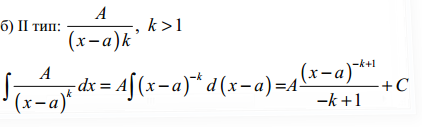
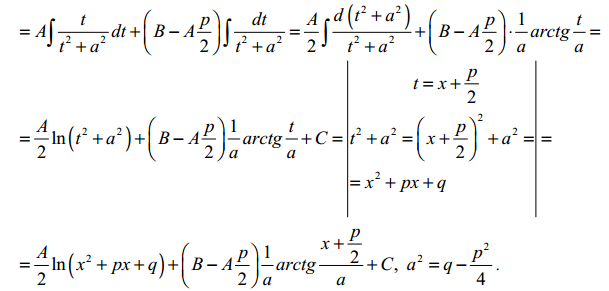
25. Інтегрування ірраціональних функцій (окрім диференціального бінома).

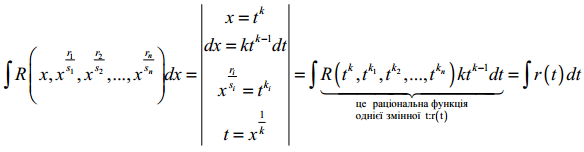
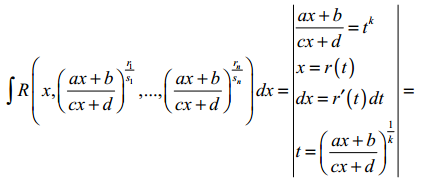
Де r_i/s_i – задані числа-дробиб i=1,n. Нехай k – спільний знаменник дробів r_i/s_i. Тоді, якщо ввести заміну x=t^k, то

26. Інтегрування тригонометричних функцій.

Будемо розглядати інтеграли, у яких підінтегральна функція є раціональною функцією змінних sin x та cos x , тобто R (sinx ,cosx).

1) універсальна підстановка t=tg(x/2), sinx = 2tg(x/2)/(1+tg²(x/2)), cosx=(1- tg²(x/2))/(1+ tg²(x/2)). 2) нехай , тоді

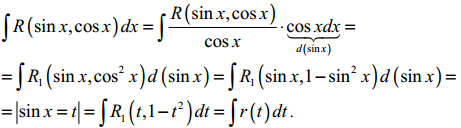
3) нехай , тоді

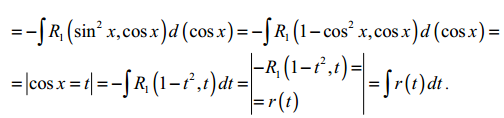
4) нехай , тоді

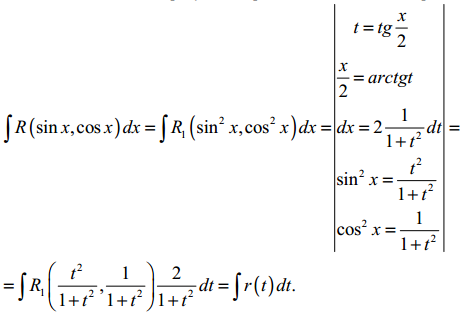
5) нехай підінтегральна функція є функцією від tg x, тобто R(tgx), тоді

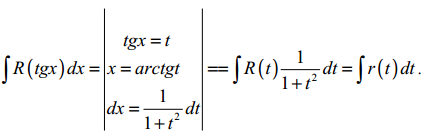
27. Визначений інтеграл. Означення. Властивості.

Якщо існує границя інтегральної суми , яка не залежить від способу розбиття відрізка [a,b] і вибору точок ξ_і , то ця границя називається визначеним інтегралом від функції f(х) на відрізку [a,b].

Властивості:

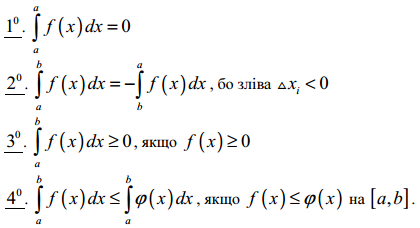
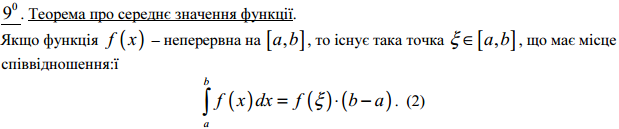
28. Формула Н’ютона-Лейбніца.­

Якщо функція f(х) неперервна на [a,b], то має місце формула: , де F(x) – первісна для функції f(x).

29. Метод заміни змінної в визначеному інтегралі.

Нехай:

1) функція f (x) неперервна на [a,b];

2) функція x =φ(t) неперервна і має неперервну похідну φ ′(t) на [α,β];

3) ∀ t ∈ [α,β] відповідні значення x∈[a,b], причому φ(α)=a, φ(β)=b.

Тоді має місце формула:

30. Інтегрування частинами в визначеному інтегралі.

Якщо функції u(x) і v(x) диференційовні на [a,b], то:

31. Інтегрування з симетричними межами інтегрування від парних та непарних функцій.

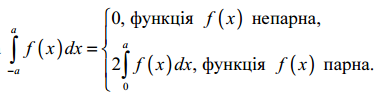32. Невласні інтеграли I роду. Означення. Аналог формули Ньютона-Лейбніца.

До невласних інтегралів І-го роду відносяться інтеграли, у яких одна чи обидві межі інтегрування є +∞ або −∞.

Вважаємо, що F(x) первісна для функції f(x) на [a,A]

33. Невласні інтеграли II роду. Означення. Аналог формули Ньютона-Лейбніца.

До невласних інтегралів ІІ роду відносяться інтеграли від необмежених функцій. Вигляд цих інтегралів такий же, як вигляд визначених інтегралів і для їх розпізнавання треба досліджувати, чи є функція f(x) необмеженою в точках відрізку інтегрування.

Нехай функція f(x) визначена на проміжку (a,b], точка x=a – особлива точка функції f(x).

Тоді невласний інтеграл ІІ роду: .

34. Застосування визначеного інтеграла. Обчислення площ та довжин дуг.

Обчислення площі криволінійної трапеції а) f(x)≥0, D: y=f(x), x=a, x=b;

; f(x) – знакозмінна, тоді .

б) нехай f(x) задана параметр. рівн. (f(x)≥0) ;

Обчислення довжини дуги

Нехай задано дугу кривої L, початок M₀, кінець M_n, розбиваємо цю дугу на частинні дуги точками M₀, M₁,…,M_n

Складаємо суму:

a) Нехай дуга AB задана парам. рівнянням:

Будемо вважати, що функції диференційовані,

б) Нехай

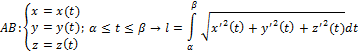
35. Частинні похідні та повний диференціал.

Якщо існує границя то ця границя називається частинною похідною від функції u(x₁,…,x_n) по змінній x_k.

Повним диференціалом функції в точці називається вираз вигляду:

36. Диференціювання функцій багатьох змінних, заданих неявно.

Нехай функція y=y(x) неявно задана рівнянням: F(x,y)=0 . Знайти dy/dx.

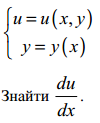
Диференціюємо рівняння F(x,y)=0 по x:

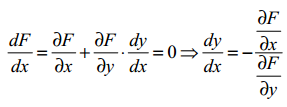
37. Необхідні та достатні умови екстремуму функцій двох змінних.

Необхідні умови: якщо функція f(x,y) диференційовна в т. M₀ та в деякому її околі і має в цій точці локальний екстремум, то

Достатні умови: нехай т.M₀ ‒ стаціонарна точка функції z=f(x,y). Тоді, якщо:

38. Подвійні та двократні інтеграли. Означення. Області правильності у напрямі осей координат.

Якщо існує границя інтегральної суми , яка не залежить від розбиття області D і вибору точок P_i, то ця границя називається подвійним інтегралом від f(x,y) по області D і позначається:

.

Область називається правильноюу напрямі осі Oy, якщо будь-яка пряма, паралельна осі Oy, перетинає межу області не більше ніж у двох точках.

Двократним(повторним) інтегралом від ф-ії f(x,y) по області D, прав. у напрямі осі Oy називають вираз:

; для Ox – зміна порядку інтегрування.

39. Обчислення подвійних інтегралів.

Якщо f(x,y) – неперервна в обл. D, яка є правильною у напрямі осі Оy, то

40. Заміна змінних у подвійному інтегралі. Загальна формула.

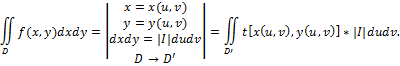
41. Перехід до полярних та узагальнених полярних координат в подвійному інтегралі.

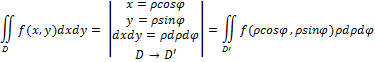
42. Потрійний та трикратний інтеграл. Означення. Поняття області, правильної у напрямі Oz.

Якщо існує границя інтегральної суми , яка не залежить від розбиття області G і вибору точок P_i, то ця границя називається потрійним інтегралом від f(x,y,z) по області G і позначається: .

Область G називається правильною у напрямі OZ, якщо:

1) будь-яка пряма l, проведена через внутр. точку області G паралельно OZ перетинає границю області G в двох точках;

2) область D_i = пр_xoyG є правильною у напрямі осі Oy(Ox).

Трикратним інтегралом від ф-ії f(x,y,z) в області G наз. вираз вигляду:

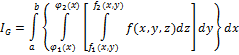
43. Обчислення потрійних інтегралів. Формула заміни змінних.

Потрійний інтеграл по області G правильної у напрямку осі OZ = трикратному інтегралу від цієї функції по області G, тобто має місце така формула:

Вважається, що функція f(x,y,z) неперервна в області G.

Формула заміни змінних:

;

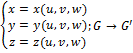44. Перехід до циліндричних координат.

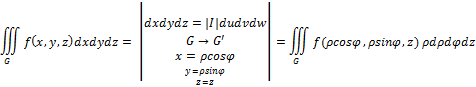
45. Перехід до сферичних координат.

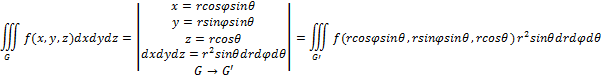
P.S.: доказательства теорем и различных формул приведены только там, где это требуется, это лишь опорная информация и не гарантирует получения максимального балла.

P.S.S.: удачи на экзамене!;)