Л1_Метричні простори_13

17

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 1

Тема: " Метричні простори. Нерівності Мінковського та Гельдера"

Дисципліна : "Функціональний аналіз"

Викладач Гусарова І. Г.

Харків,2013

Вступ. Функціональний аналіз(ФА), частина сучасної математики, головним завданням якої є вивчення безконечномірних просторів і їх відображень. Найбільш вивчені лінійні простори і лінійні відображення. Для ФА характерне поєднання методів класичного аналізу, топології і алгебри. Абстрагуючись від конкретних ситуацій, удається виділити аксіоми і на їх основі побудувати теорії, що включають класичні завдання як окремий випадок і що дають можливість вирішувати нові завдання. Сам процес абстрагування має самостійне значення, прояснюючи ситуацію, відкидаючи зайве і відкриваючи несподівані зв'язки. В результаті удається глибше проникнути в суть математичних понять і прокласти нові дороги дослідження.

Розвиток ФА відбувався паралельно з розвитком сучасної теоретичної фізики, при цьому з'ясувалося, що мова ФА найадекватніше відображає закономірності квантової механіки, квантової теорії поля і т.п. У свою чергу ці фізичні теорії зробили істотний вплив на проблематику і методи ФА.

Виникнення функціонального аналізу. ФА як самостійний розділ математики склався на рубежі 19 і 20 вв.(століття) Велику роль у формуванні загальних понять ФА зіграла створена Р. Кантором теорія безлічі. Розвиток цієї теорії, а також аксіоматичній геометрії привело до виникнення в роботах М. Фреше і Ф. Хаусдорфа метричною і загальнішою т.з. теоретико-множинній топології, що вивчає абстрактні простори, тобто безліч довільних елементів, для яких встановлено тим або іншим способом поняття близькості.

  Серед абстрактних просторів для математичного аналізу і ФА виявилися важливими функціональні простори (тобто простори, елементами яких є функції — звідки і назва «ФА»). У роботах Д. Гильберта по поглибленню теорії інтегральних рівнянь виникли простори l ₂ і L ₂ ( а , b ) (див. нижче). Узагальнюючи ці простори, Ф. Рис вивчив простори l _p і L _p ( а , b ), а С.Банах в 1922 виділив повні лінійні нормовані простори (банахови простори). У 1930—40-х рр. в роботах Т. Карлеману, Ф. Рису, американських математиків М. Стоуна і Дж. Неймана була побудована абстрактна теорія самосопряжених операторів в Гільбертовому просторі.

  В СРСР перші дослідження по ФА з'явилися в 30-х гг., це роботи: А. Н. Колмогорова (1934) по теорії лінійних топологічних просторів; Н. Н. Боголюбова (1936) по інваріантних заходах в динамічних системах; Л. С. Канторовіча (1937) і його учнів по теорії напіввпорядкованих просторів, вживанням ФА до обчислювальної математики і др.; М. Г. Крейна і його учнів (1938) по поглибленому вивченню геометрії Банахових просторів, опуклої безлічі і конусів в них, теорії операторів і зв'язків з різними проблемами класичного математичного аналізу і др.; І. М. Гельфанда і його учнів (1940) по теорії нормованих кілець (Банахової алгебри) і ін.

  Для сучасного етапу розвитку ФА характерне посилення зв'язків з теоретичною фізикою, а також з різними розділами класичного аналізу і алгебри, наприклад теорією функцій багатьох комплексних змінних, теорією диференціальних рівнянь з частинними похідними і т.п.

Тема: Метричні простори. Нерівності Мінковського та Гельдера

1 Метричні простори

Означення: Метричним простором називається пара , що складається з деякої множини (простору) елементів (точок) та відстані, тобто однозначної, невід’ємної, дійсної функції , що визначена для будь-яких та з і задовольняє наступним трьом аксіомам:

1) тоді і тільки тоді, коли ,

2) (аксіома симетрії): ,

3) (аксіома трикутника): .

Ці аксіоми називаються аксіомами метрики.

Сам метричний простір, тобто пару , будемо позначати, як правило, однією буквою:

.

У випадках, коли непорозуміння виключені, будемо позначати метричний простір тим же символом, що і множину точок .

Наведемо приклади метричних просторів:

1. Покладемо для елементів довільної множини

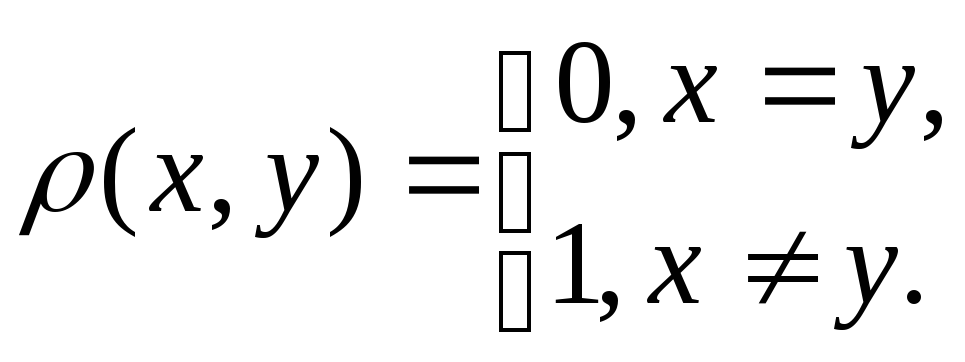
Таким чином, отримаємо метричний простір, який можна назвати простором ізольованих точок або дискретним простором.

2. Множина дійсних чисел з відстанню

утворює метричний простір .

3. Множина впорядкованих груп з дійсних чисел

з відстанню, що задається наступною формулою:

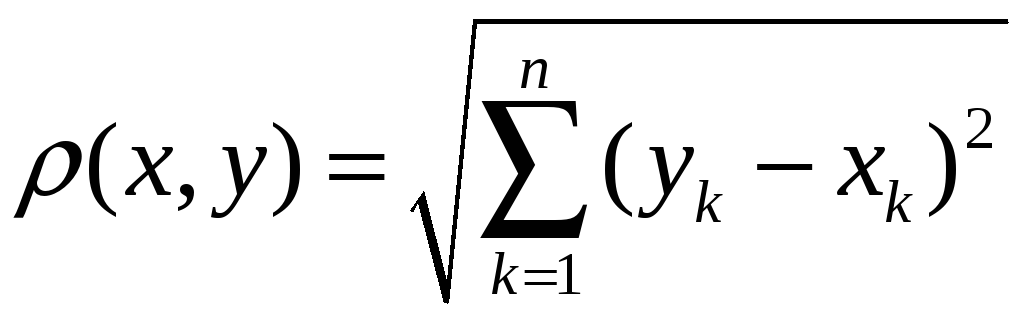(1)

називається n-вимірним арифметичним евклідовим простором .

Перевіримо виконання аксіом метрики.

Аксіома 1): Нехай

.

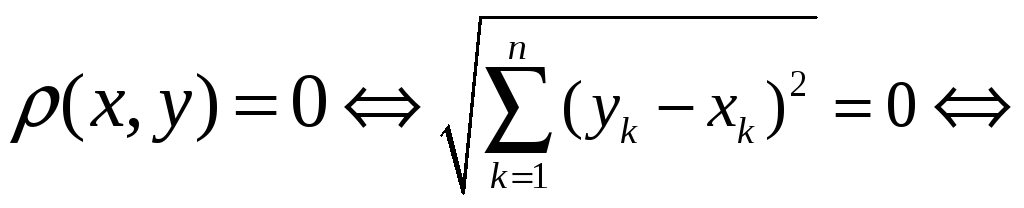
Аксіома 2): .

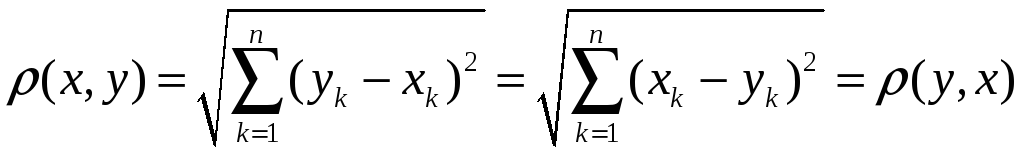Покажемо, що в виконується і аксіома трикутника.

Нехай , та . Тоді аксіома трикутника запишеться у вигляді:

. (2)

Нехай , , одержимо , і нерівність приймає вигляд

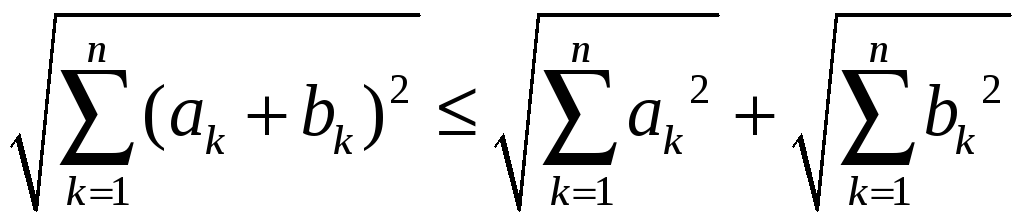. (3)

Ця нерівність є наслідком нерівності Коші—Буняковського:

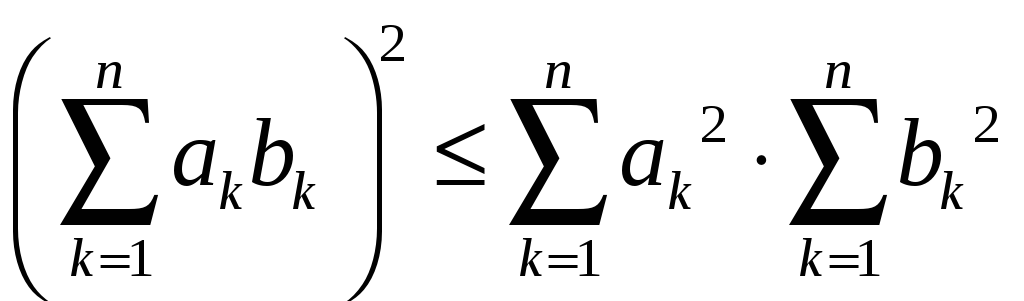. (4)

Дійсно, в силу цієї нерівності маємо

;

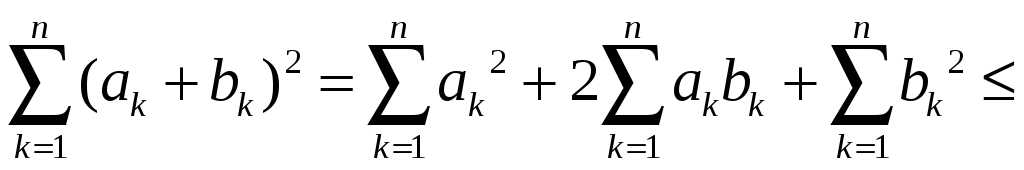
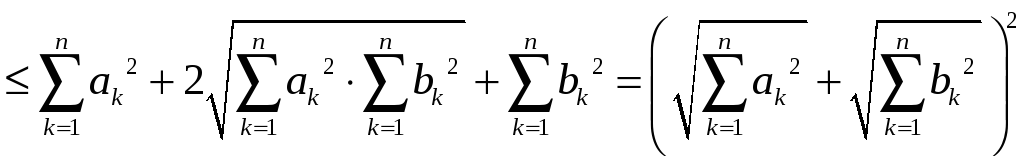Таким чином нерівність (3), а звідси і (2), доведені.

Нерівність Коші—Буняковського випливає з тотожності

,

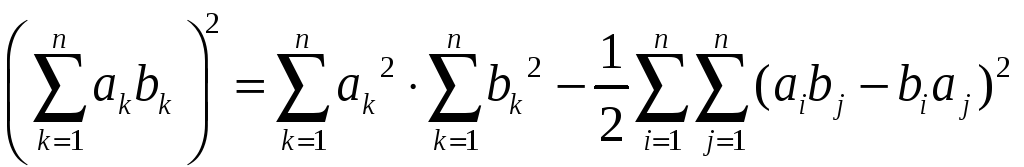яка безпосередньо перевіряється.

4. Розглянемо ту ж саму множину впорядкованих наборів з дійсних чисел , але відстань в них визначимо формулою

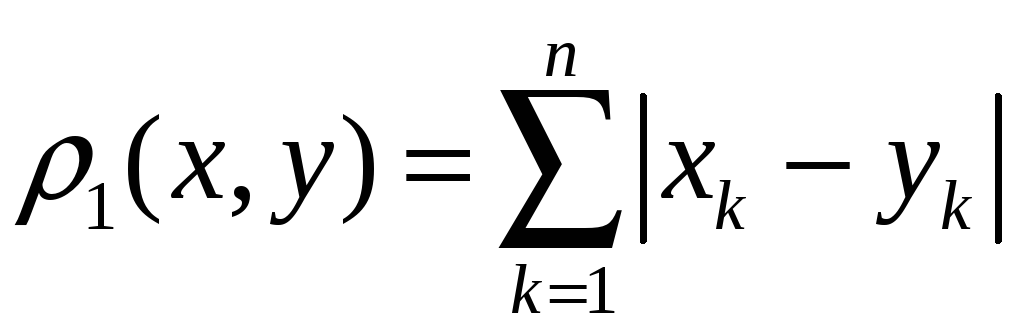. (5)

Справедливість аксіом 1)-3) очевидна. Позначимо цей метричний простір символом .

5. Розглянемо ту ж саму множину, що і в прикладах 3. та 4., і визначимо відстань між його елементами як

. (6)

Справедливість аксіом 1)-3) очевидна. Позначимо цей метричний простір символом .

Останні три приклади показують, що іноді важливо мати різні позначення для самого метричного простору та для множини його елементів, так як одна і та ж множина точок може бути по-різному метризована.

6. Множина всіх неперервних функцій, що задані на сегменті з відстанню

(7)

також утворює метричний простір. Аксіоми 1)-3) перевіряються безпосередньо. Цей простір грає дуже важливу роль в аналізі. Будемо позначати простір тим же символом , що і множину його точок. Замість зазвичай пишеться просто .

7. Позначимо через метричний простір, точками якого служать всілякі послідовності

дійсних чисел, які задовольняють умові

,

а відстань задається формулою

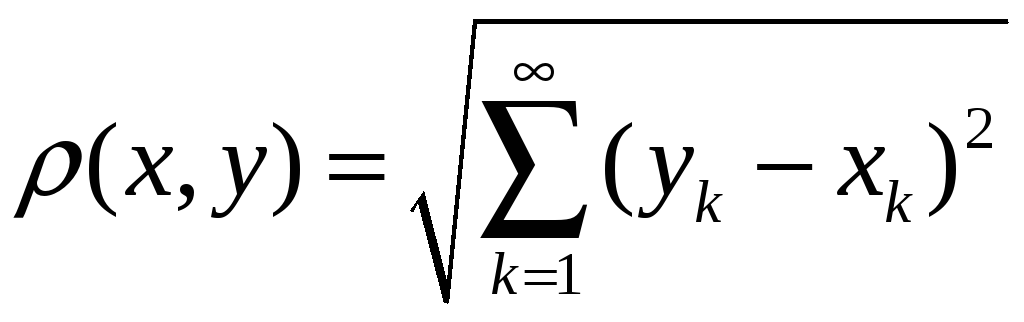. (8)

З елементарної нерівності

слідує, що функція має зміст для усіх , тобто ряд 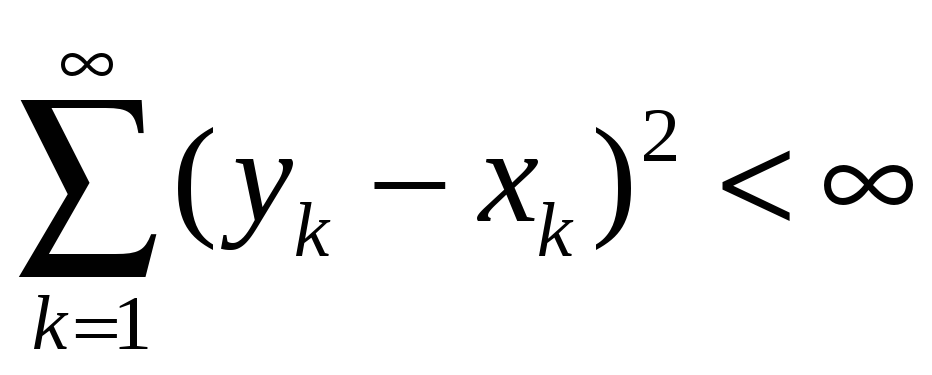збігається, якщо

та .

Покажемо, що функція відстані (8) задовольняє аксіомам метричного простору. Аксіоми 1) та 2) очевидні, а аксіома трикутника набуває вигляду

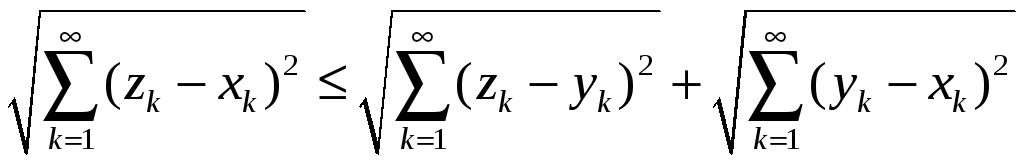. (9)

В силу сказаного вище кожен з трьох написаних рядів збіжний, крім того, при будь-якому справедлива нерівність

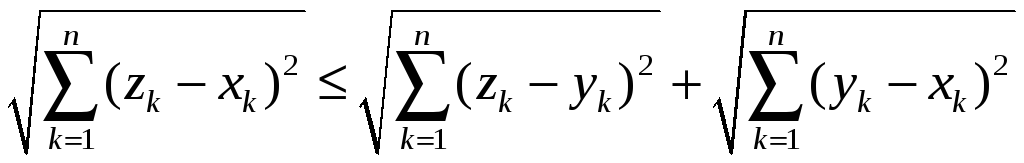
(див. приклад 3). Перейшовши до границі при , отримуємо нерівність трикутника (9) в .

8. Розглянемо простір функцій, неперервних на сегменті , що інтегруються з квадратом:

.

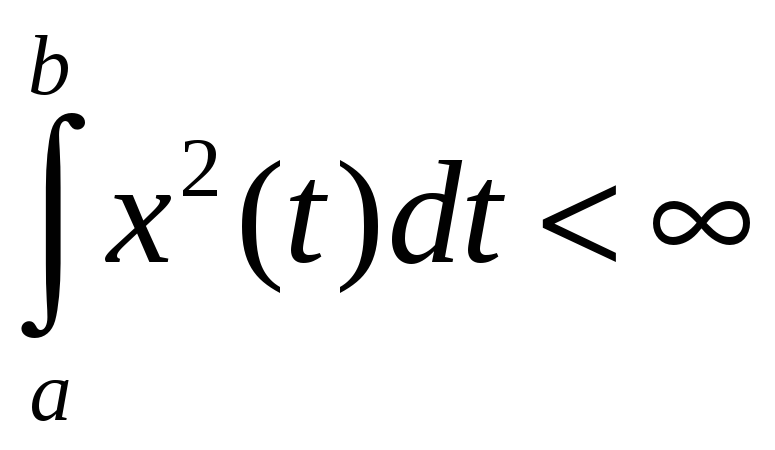Відстань визначимо наступним чином:

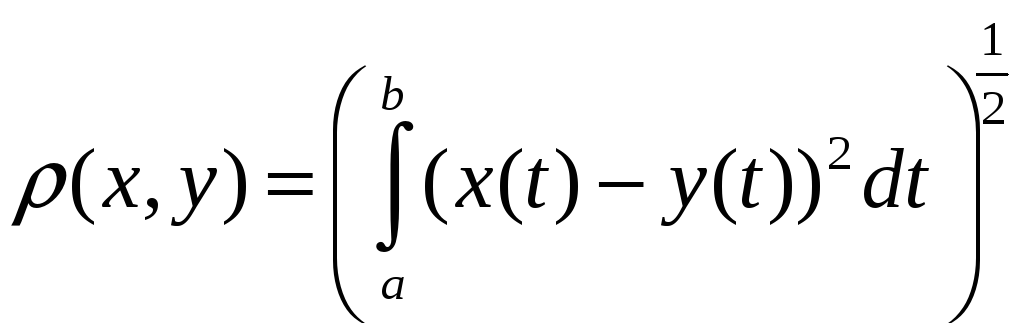. (10)

Такий метричний простір позначимо і назвемо простором неперервних функцій з квадратичною метрикою. Аксіоми 1) та 2) тут очевидні, а аксіома трикутника безпосередньо випливає з нерівності Коші—Буняковского

.

9. Розглянемо множину всіх обмежених послідовностей дійсних чисел, тобто таких, що

.

Візьмемо

. (11)

Отримаємо метричний простір, який позначимо через . Справедливість аксіом 1)-3) очевидна.

10. Множина впорядкованих груп з дійсних чисел з відстанню

, (12)

де - будь-яке фіксоване число , представляє собою метричний простір, який позначимо як . Покладемо

, ,

тоді нерівність

,

справедливість якої маємо встановити, прийме вигляд

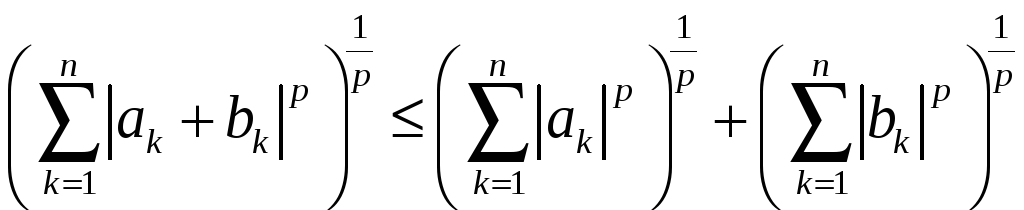. (13)

Це – нерівність Мінковського. При нерівність очевидна (модуль суми не більше за суму модулів), тому вважаємо .

Якщо доведемо нерівність Мінковського, то буде виконана аксіома трикутника у просторі .

Розглянута в цьому прикладі метрика перетворюється у евклідову метрику (приклад 3) при і в метрику приклада 4 при . Можна показати, що метрика , яка розглянута у прикладі 5, є граничним випадком метрики , а саме

.

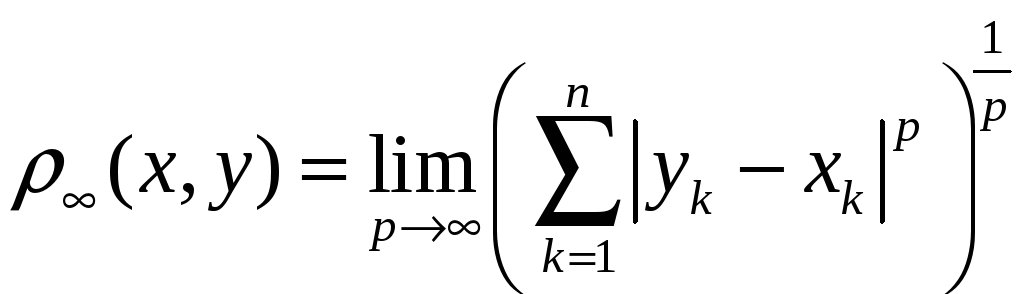11. Вкажемо ще один цікавий приклад метричного простору. Його елементами є всілякі послідовності чисел

,

такі, що

,

де - деяке фіксоване число, а відстань визначається формулою

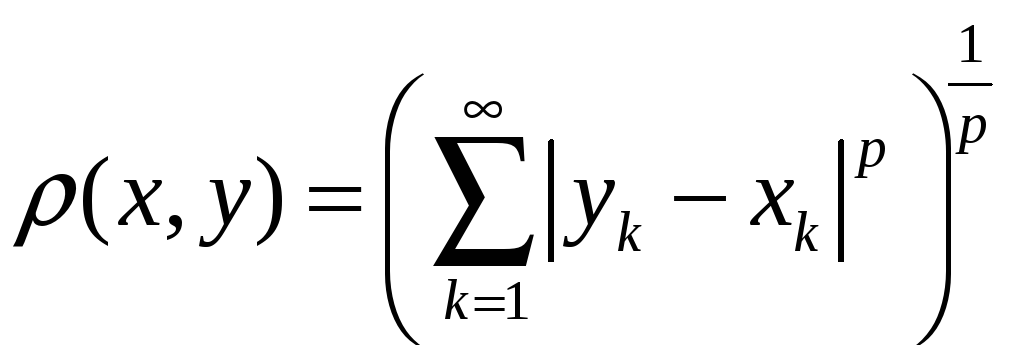. (14)

Цей метричний простір позначимо .

В силу нерівності Мінковського маємо при будь-якому

.

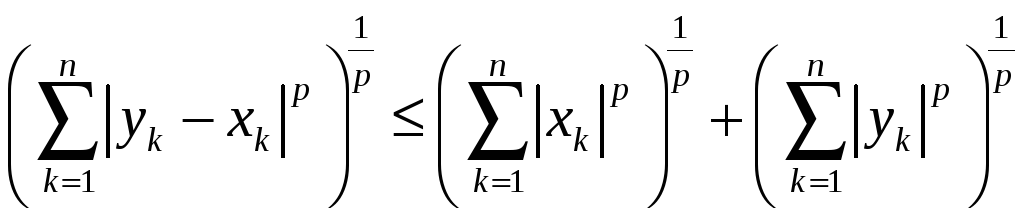Так як, за припущенням, ряди

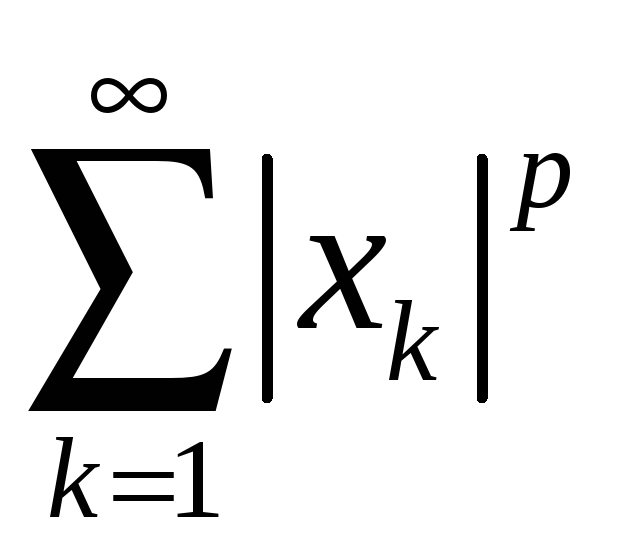та

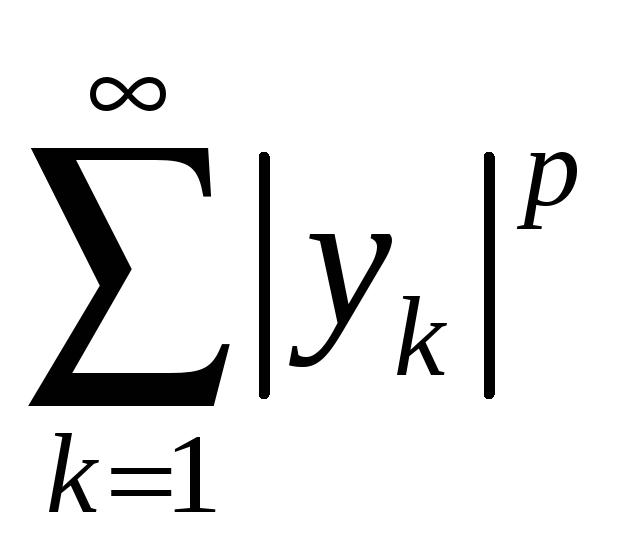
збігаються, то, здійснивши перехід до границі при , отримаємо

(15)

Таким чином, доведено, що формула (14), яка визначає відстань в , дійсно має зміст для будь-яких . Одночасно нерівність (15) показує, що в виконана аксіома трикутника. Інші аксіоми очевидні.

2 Нерівность Гельдера

Доведення нерівності (13) засноване на нерівності Гельдера:

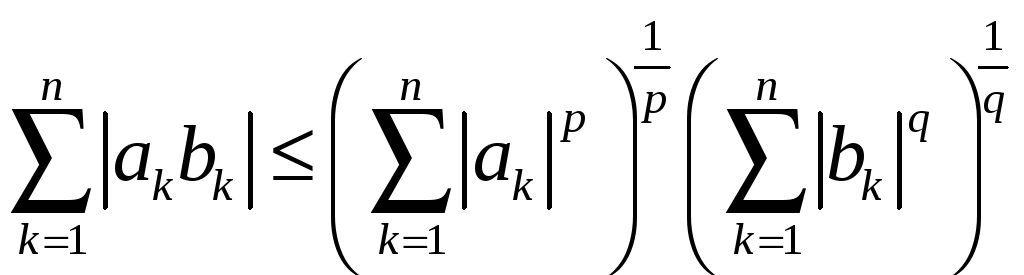, (16)

де числа та пов’язані умовою

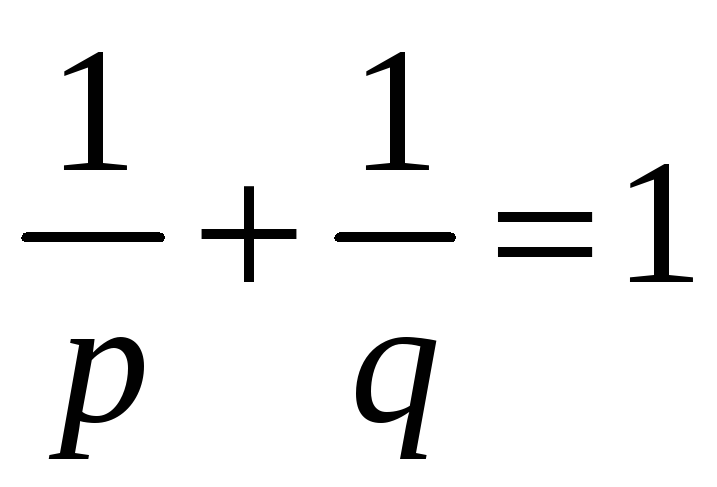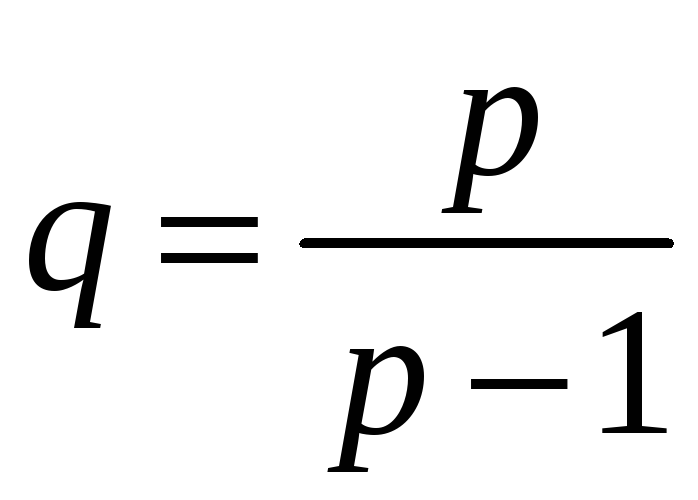, тобто . (17)

Нерівність (16) однорідна, а це означає, що якщо вона виконується для будь-яких векторів та , то вона виконується й для векторів та , де і - довільні числа. Тому цю нерівність достатньо довести для випадку, коли

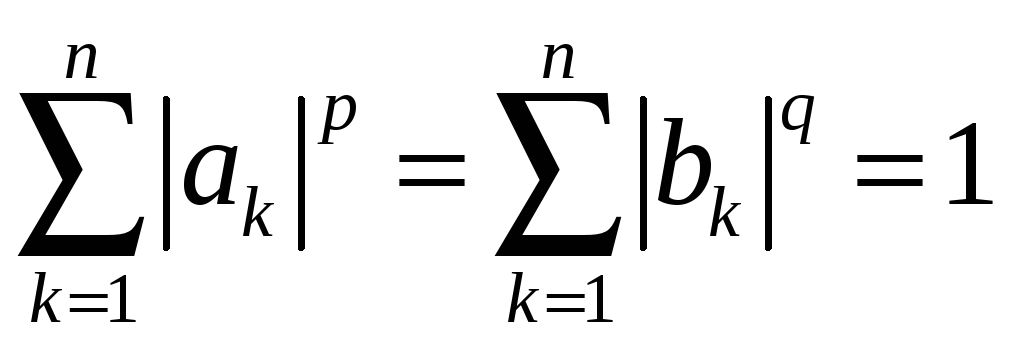. (18)

Нехай виконана умова (18). Доведемо, що

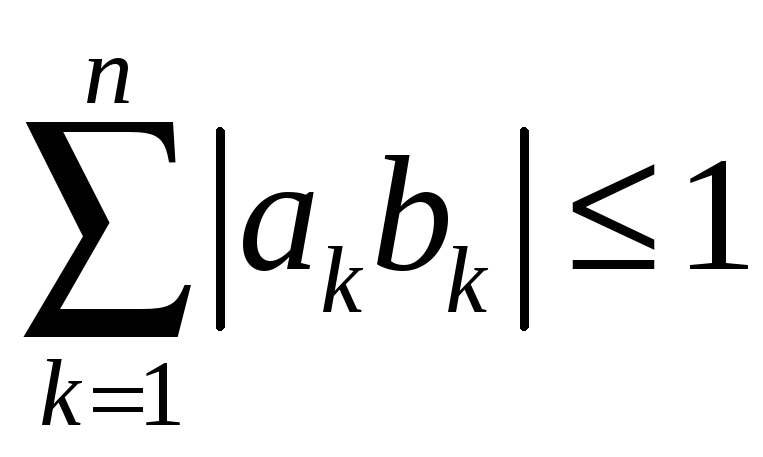. (19)

Розглянемо на площині криву, що визначена рівнянням , або .

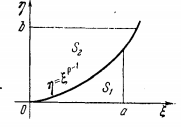
Рис. 1

З рис. 1 ясно, що при будь-якому виборі додатних значень і буде . Обчислимо площі і :

; .

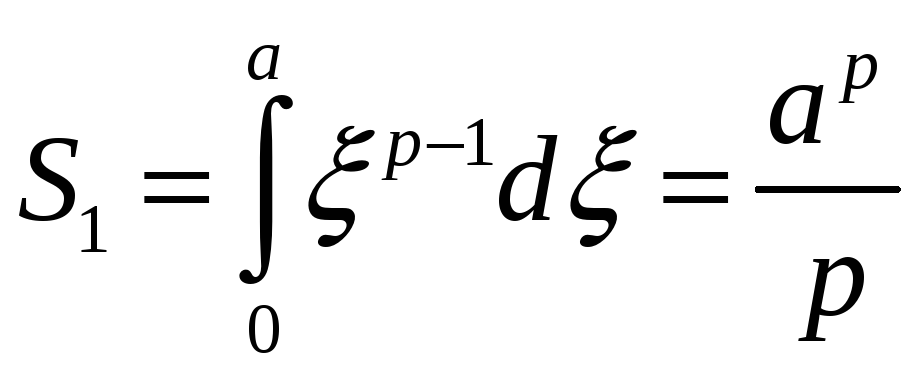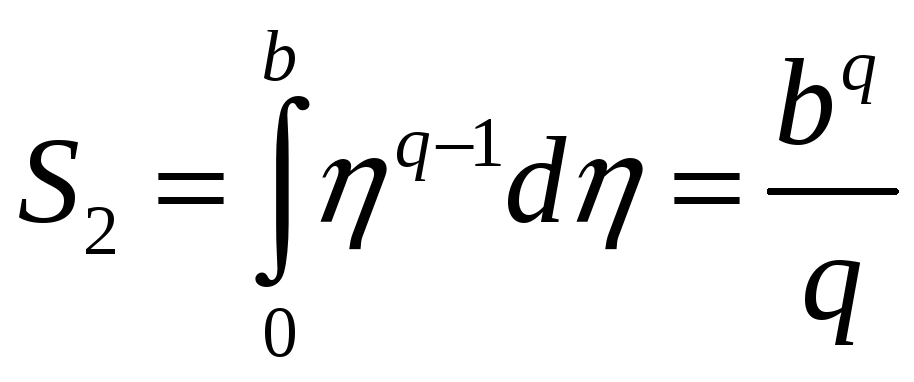Таким чином, справедлива числова нерівність

.

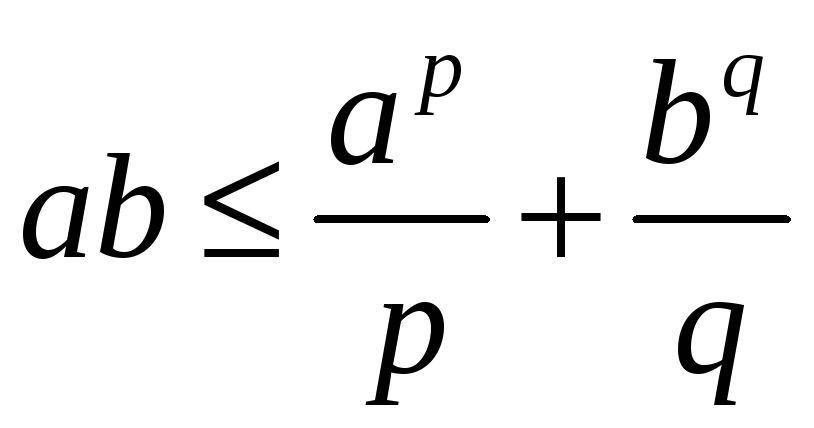Замінивши на , на , і знайшовши суми по від 1 до , одержимо, врахувавши (17) та (18), , а звідси і нерівність Гельдера доведено. При нерівність Гельдера (16) переходить в нерівність Коші—Буняковського (4).

3 Нерівності Мінковського

Тепер перейдемо до доведення нерівності Мінковського. Для цього розглянемо тотожність

.

Замінивши на , на , і підсумувавши по від 1 до , одержимо

.

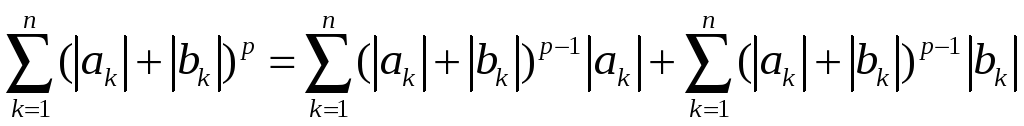Тепер застосуємо нерівність Гельдера, і, прийнявши до уваги, що , маємо

.

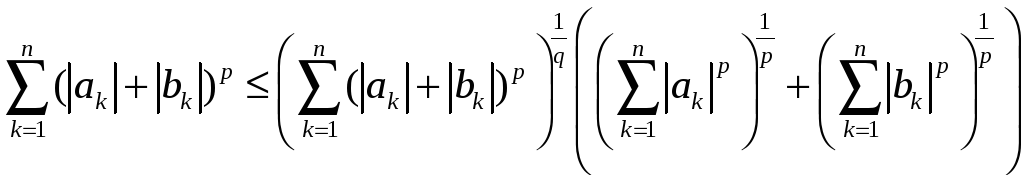Поділивши обидві частини нерівності на

,

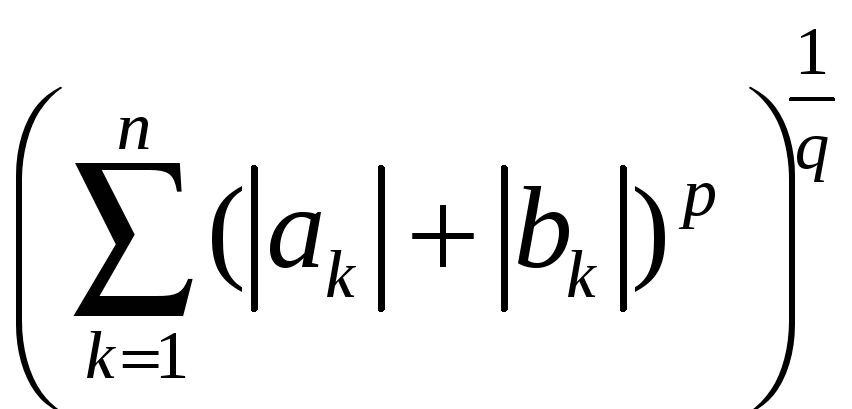отримаємо

,

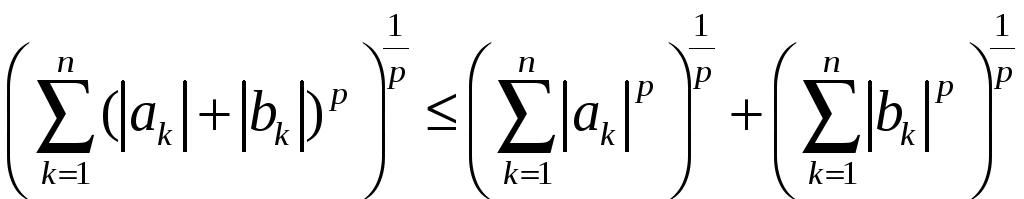звідки відразу випливає нерівність (13). Тим самим встановлена аксіома трикутника у просторі .

З нерівності

,

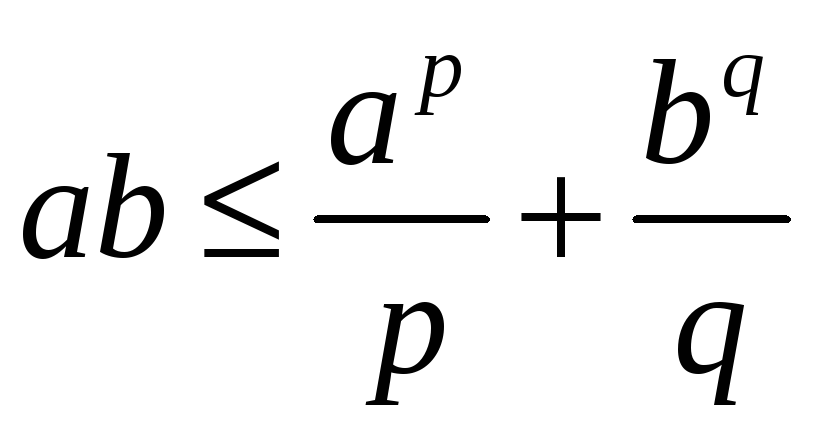
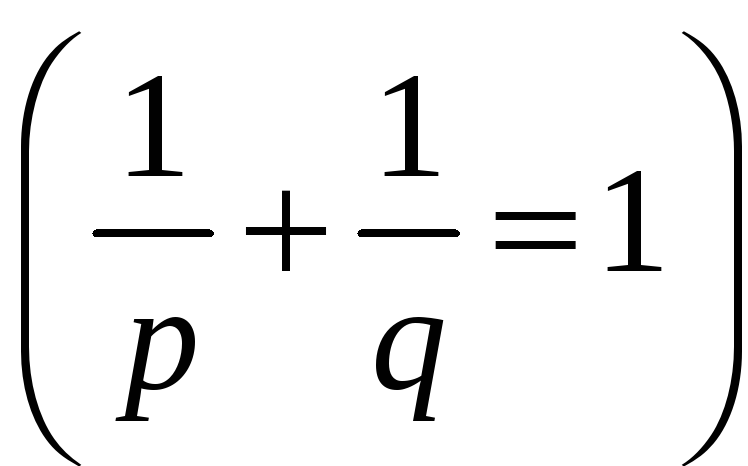встановленої вище, легко виводиться і інтегральна нерівність Гельдера

,

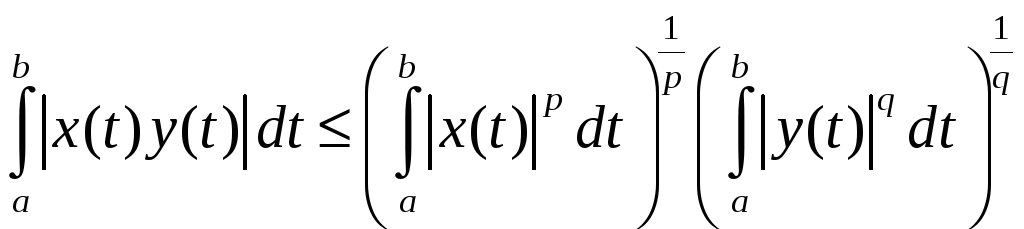справедлива для будь-яких функцій та , для яких інтеграли, що стоять справа, мають зміст. Звідси в свою чергу маємо інтегральну нерівність Мінковського

.

Індивідуальні завдання.

1. Довести, що множина всіляких послідовностей чисел

,таких, що , а відстань визначається формулою є метричним простором .

2. Навести приклад відстані між елементами множини всіх студентів групи СА-13-1 , щоб зробити цю множину метричним простором.

3. Довести, що множина всіх дійсних чисел з відстанню є метричним простором.

4. Знайти відстань між елементами і в просторах , , , , якщо

1).,,; 2). ,,;

3).,,; 4).,,;

5).,,; 6). ,,;

7). ,,; 8) ,,.

Литература

1. Тевяшев А. Д., Головко Н.А.Функціональний аналіз у прикладах та задачах: Навч.посібник.-Харків:ХТУРЕ,1998.-140с.

2. Колмогоров А.Н., Фомин С.В.Элементы теории функций и функционального анализа. - 8-е изд.Издательство: Физматлит, 2012-572с.

3. Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа: Учебное пособие.2-е изд.,стер.,2009. – 272с.

4. Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа. – М.: Наука, 1988.

5. Городецкий В.В., Нагнибида Н.И., Настасиев П.П.Методы решения задач по функциональному анализу.-Издательство:Книжный дом "ЛИБРОКОМ", 2012.-480с.

6. Князев П.Н. Функциональный анализ : учеб. пособие/ П.Н. Князев. –

7. 3-е изд. - М.: ЛИБРОКОМ, 2009. - 206 с.