3 Исследование возможностей использования критериев множественных сравнений при распознавании патологических процессов

3.1 Цель работы

Изучение возможностей использования непараметрических критериев сравнения более чем двух независимых или зависимых выборок при распознавании патологических процессов с помощью SPSS и Microsoft Excel.

3.2 Методические указания по организации самостоятельной работы студентов

При подготовке к лабораторной работе необходимо изучить особенности непараметрических тестов, применяемых для сравнения более чем двух независимых или зависимых выборок, возможности SPSS и Microsoft Excel при проверке гипотез о положении и рассеивании [1 – 4].

Довольно часто возникает ситуация, когда необходимо сравнить между собой не два значения средних, а несколько. Сравнение с помощью дисперсионного анализа позволяет выяснить, можем ли мы считать их равными. Если они неравны, необходимо выяснить, какие средние значения равны между собой, а какие отличаются, а также какие группы средних значений равны между собой, а какие нет. Это позволяет сделать метод множественных сравнений Шефе (другое название – заключение о линейных контрастах по Шефе) и LSD критерий.

Проверяется гипотеза о принадлежности нескольких средних значений к одной генеральной совокупности или выделение групп средних значений, принадлежащих к одной совокупности.

, (3.1)

где С_i – определенные константы, на которые накладывается условие .

Контрастом называется линейная комбинация средних значений выборок. Допустим, у нас имеется 5 выборок, средние значения которых ,,,и. Предположим, что эти выборки принадлежат к двум разным генеральным совокупностям, средние значения в которыхисоответственно. Тогда нулевую гипотезу можно сформулирована в виде. При этом в зависимости от состава выборок, из которых могут состоять группыА и В, возможны такие конкретные варианты этой гипотезы:

,

и т.д.

Так как часто проверяют не группы, а отдельно взятые выборки, то сравнивая между собой, например, средние первой и четвертой выборок, коэффициенты С_i будут иметь такие значения: 1, 0, 0,-1,0. Изменяя C_i, можно проверить любые комбинации пар выборок. Критериальное значение Шефе рассчитывается по формуле

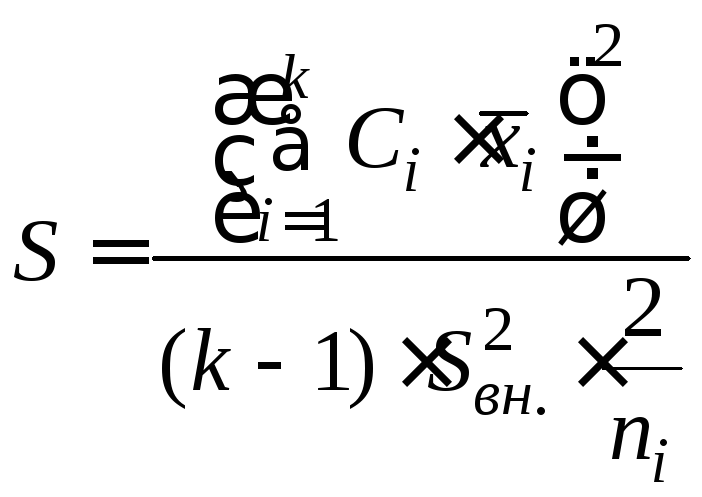. (3.2)

При этом внутригрупповая дисперсия рассчитывается по формуле

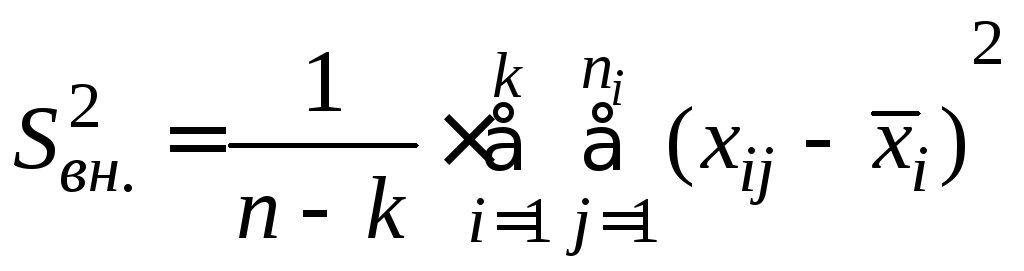, (3.3)

где ;

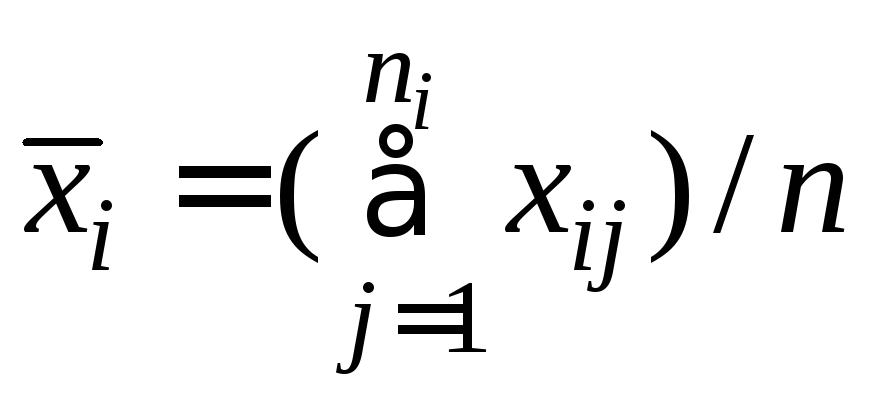k – число выборок;

n_i – количество наблюдений в каждой выборке;

n= – общее количество наблюдений.

Если рассчитанное значение S будет больше критического значения распределения , то гипотеза о равенстве средних соответствующих выборок или групп выборок отвергается.

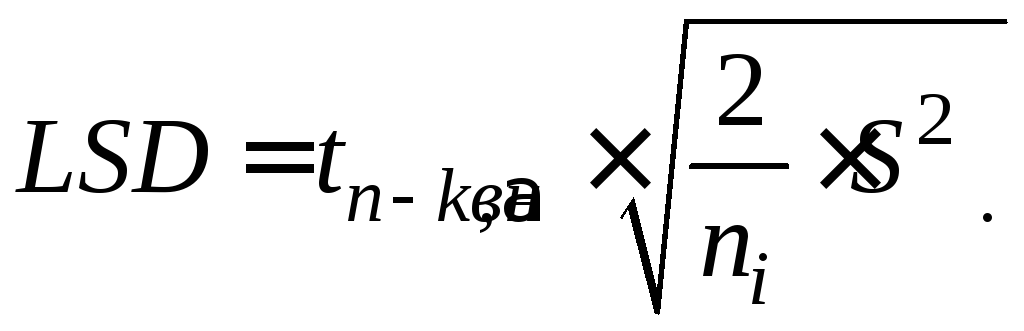, (3.4)

где – табличное значение критерия Стьюдента;

–внутригрупповая дисперсия;

–количество наблюдений в каждой выборке.

Это значение используется для проверок всех пар.

Если разница средних значений соседней пары меньше значения LSD, то эти средние значения считаются одинаковыми, а соответствующие выборки объединяют в однородную группу.

Пример 1. Из общей генеральной совокупности пациентов, страдающих ИБС, было выделено пять групп пациентов, проходящих обследование в различных клиниках: «Группа 1», «Группа 2», …, «Группа 5». Определить принадлежность средних значений возраста пациентов в пяти группах (выборках) к одной генеральной совокупности и выделить однородные группы средних значений возраста пациентов, страдающих ИБС.

Для решения задачи составим таблицу (рис. 3.1), где в ячейках B1:F14 размещены исходные данные нашей задачи.

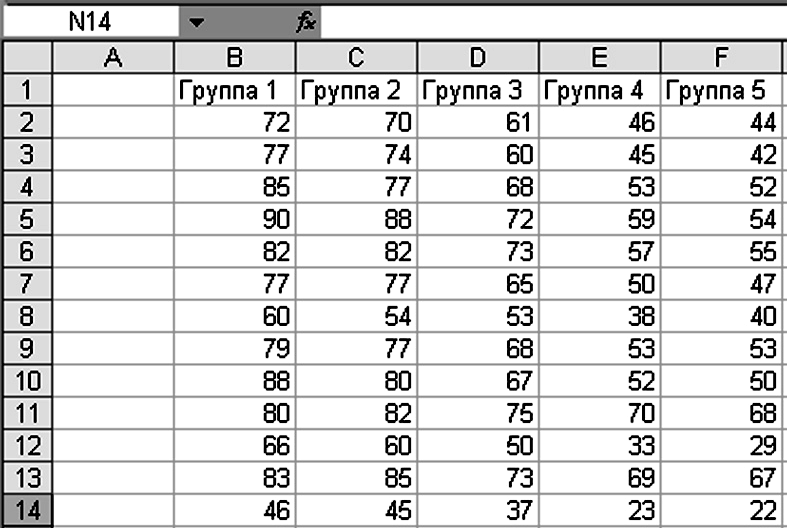
Рисунок 3.1 – Размещение исходных данных на рабочем листе Excel

Проведем предварительную обработку исходных данных (рис. 3.2). Определим средние значения возраста пациентов для каждой из пяти групп с помощью функции СРЗНАЧ, (например, для группы 1 среднее арифметическое рассчитывается как «=СРЗНАЧ(В2:В14)=75,769».

Проверим, распределены ли выборки по нормальному закону, используя встроенную функцию NORMSAMP_1 (для группы 1 запись функции проверки на нормальность распределения будет такой: «= NORMSAMP_1(В2:В14)= =NORM»).

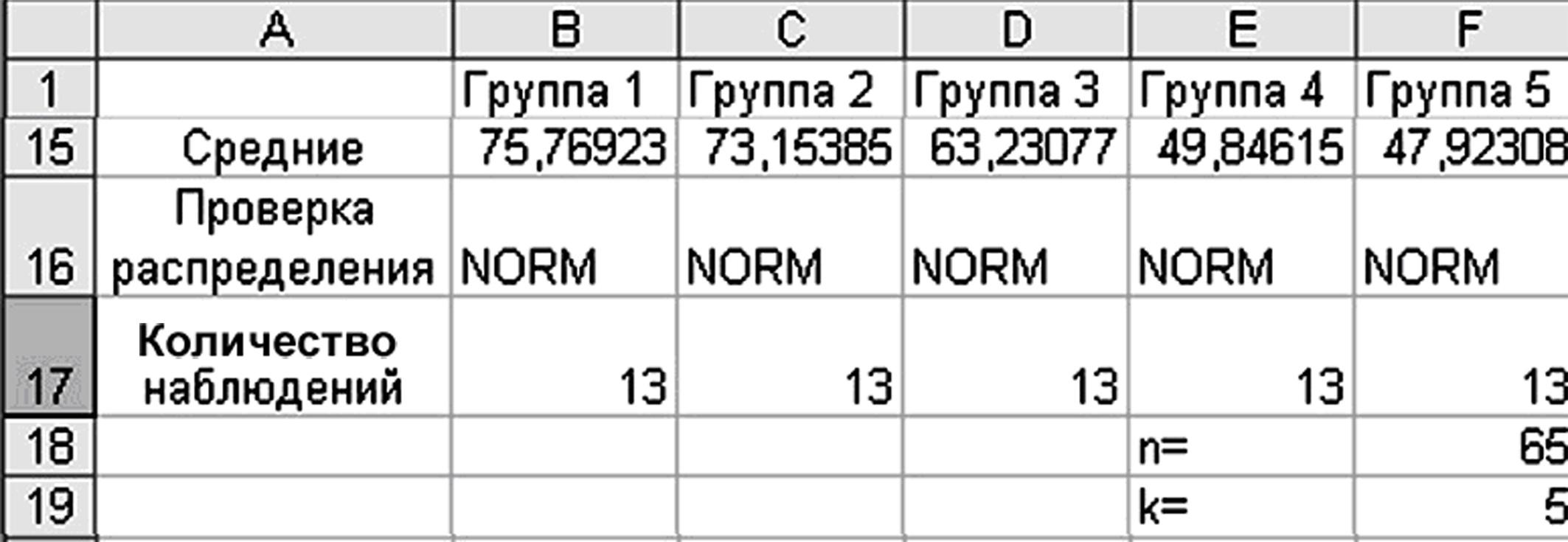
Рисунок 3.2 – Предварительные расчеты по исходным данным

Определим количество наблюдений в каждой выборке, используя функцию ЧСТРОК, «=ЧСТРОК(В2:В14)=13», общее количество наблюдений n с помощью функции СУММ, «=СУММ(В17:F17)=65» и с помощью функции ЧИСЛСТОЛБ общее число выборок k, «=ЧИСЛСТОЛБ(В2:F2)=5».

Рассчитаем внутригрупповую дисперсию . Для этого сформируем вспомогательную матрицу дисперсий, рассчитаем в свободной ячейке формулу «=(В2-В$15)*(В2-В$15)=14,21» и размножим ее на все ячейки исследуемого диапазона (рис. 3.3).

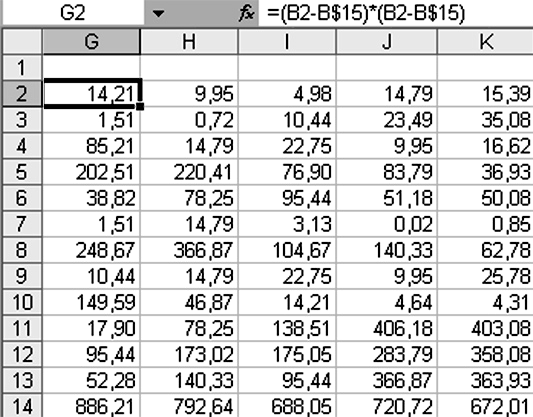
Рисунок 3.3 – Вспомогательная матрица дисперсий

Находим внутригрупповую дисперсию, поместив в свободную ячейку формулу «= СУММ(G2:K14)/(F18-F19)=9368,923/60=156,15» (рис. 3.4).

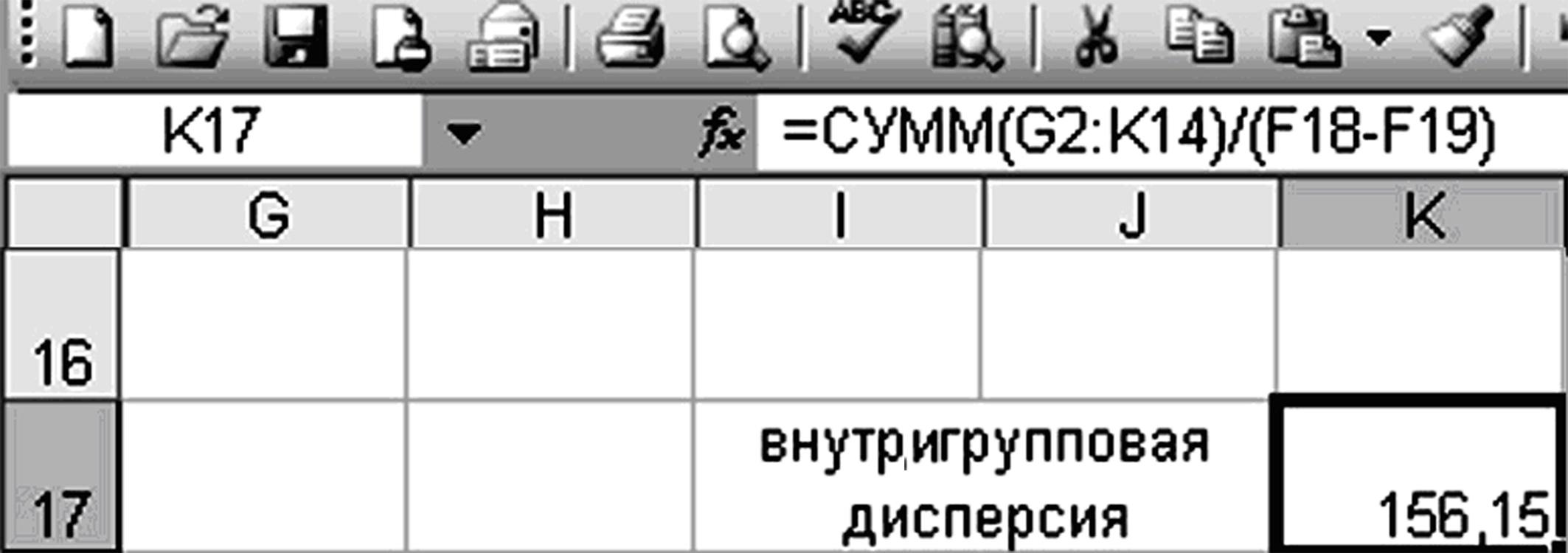
Рисунок 3.4 – Расчет внутригрупповой дисперсии

Выполним попарные сравнения всех средних. Для этого создадим матрицу коэффициентов С_i, которая строится методом простого перебора всех вариантов комбинаций (рис. 3.5).

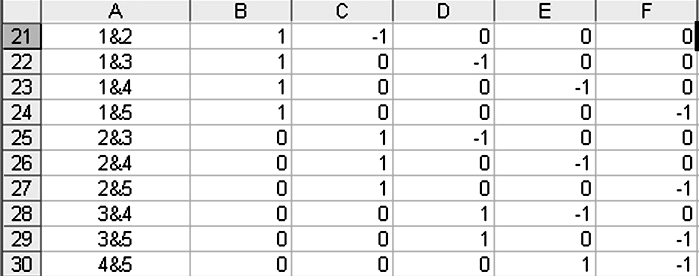
Рисунок 3.5 – Матрица коэффициентов С_i

Определим константы (). Для этого с помощью матрицысоздаем вспомогательную матрицуG21:K30 (рис. 3.6), помещая в свободную ячейку G21 формулу «=(В21·В$15)=75,769», которую затем размножаем, перетягивая на все ячейки указанного диапазона.

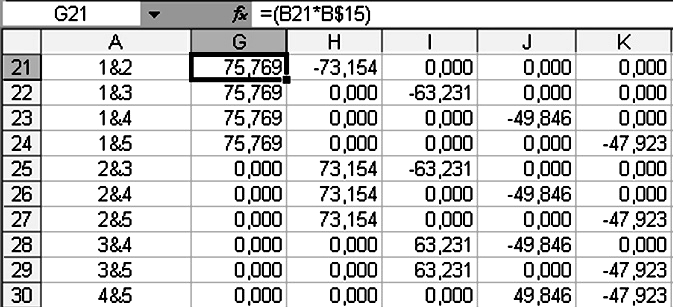
Рисунок 3.6 – Вспомогательная матрица коэффициентов

Найдем критериальное значение Шефе S для каждой сравниваемой пары.

Для этого в пустую ячейку N21 поместим формулу «=M21/(($F$19 –1)· ·$K$17·2/B$17)=0,071» (рис. 3.7), которую копируем на весь столбец.

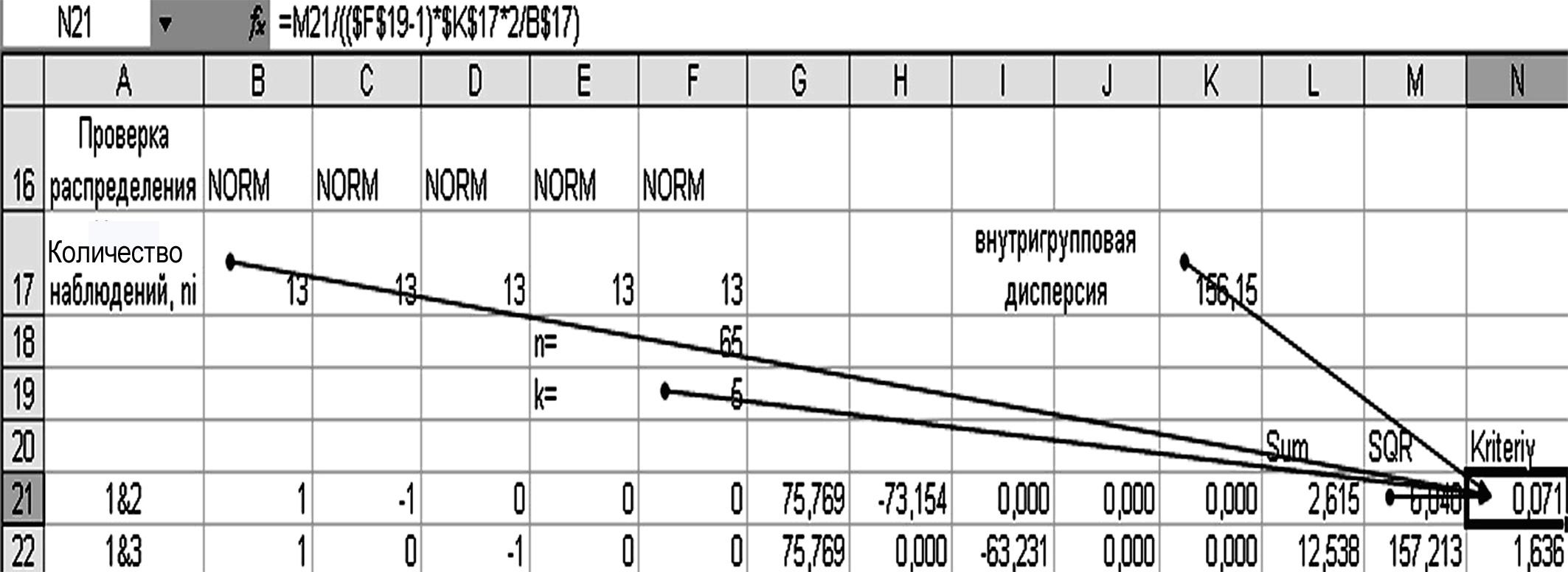
Рисунок 3.7 – Расчет критериального значения Шефе S

Для проверки гипотезы о равенстве средних возрастов пациентов в пяти группах рассчитаем критическое значение F-распределения , используя функцию «=FРАСПОБР(0,05; F19-1;F18-F19)=2,525» (рис. 3.8).

Рисунок 3.8 – Расчет критического значения F-распределения

Сравним полученное критическое значение с рассчитанным значениемS для каждой пары средних сравниваемых групп (рис. 3.9).

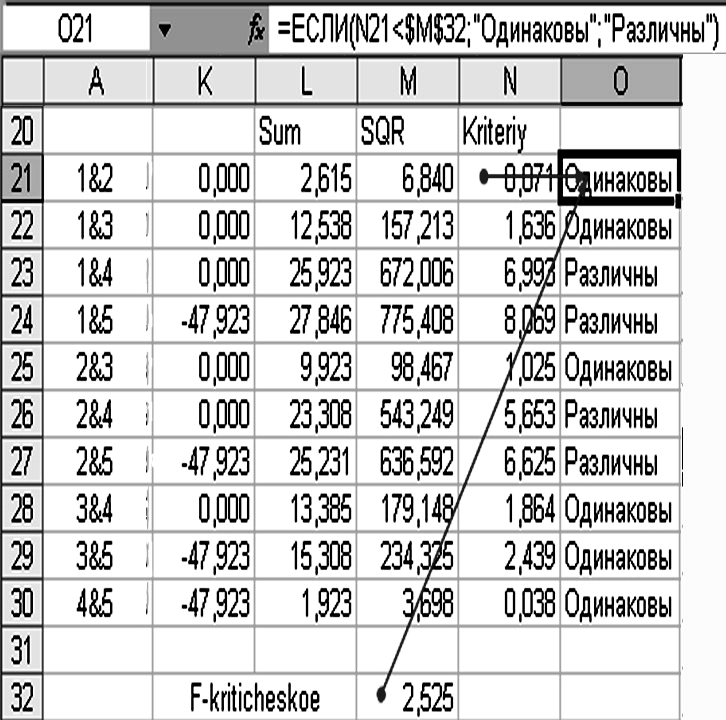
Рисунок 3.9 – Проверка гипотезы о равенстве средних значений групп выборок

Для этого в свободную ячейку, рядом со значением критерия Шефе для первой пары, помещаем формулу «=ЕСЛИ (N21< $M$32; ”Одинаковы“; ”Различны“) = ОДИНАКОВЫ» и копируем ее в ячейки для всех остальных пар.

Проведем распределение средних значений возраста пациентов по однородным группам. Для этого рассчитываем значение LSD, для чего в пустую ячейку под критическим значением F-распределения помещаем формулу «=СТЬЮДРАСПОБР (0,05; F18-F19) * КОРЕНЬ (2*K17/B17) = 9,804» (рис. 3.10).

Рисунок 3.10 – Распределение средних значений в однородные группы

Из сравнения видно, что средние значения возраста пациентов пяти групп распадаются на три однородные группы. В первую группу входят первая и вторая группы выборок значений из общей генеральной совокупности, во вторую однородную группу входит третья выборка, четвертая и пятая выборка составляют третью однородную группу.

Непараметрические критерии применяются в тех случаях, если закон распределения отличается от нормального, или данные измеряют в дискретных шкалах измерений.

Для множественных сравнений имеются непараметрические критерии, которые выполняют ту же или сходную задачу, что и критерий Шефе. К ним относятся и множественные сравнения, основанные на суммах рангов Фридмана.

Пусть имеется k выборок, в каждой из которых есть n наблюдений. То есть мы имеем матрицу исходных данных, в которой n строк и k столбцов. Построим ранги для каждой строки матрицы. Сумма рангов для каждого столбца вычисляется как

, (3.5)

где r_ij – ранг i-го наблюдения в j-й выборке.

После этого строится разностей между суммами рангов, взятых по абсолютной величине.

Если выполняется условие , то с уровнем значимости α можно считать, что средние значения выборок с номерамиu и v не равны.

Каждому значению соответствует свое значениеα (табл. В.4). Это связано с тем, что значения дискретны и рассчитываются по комбинаторным формулам для каждого сочетанияn и k. Значение α при этом выбирается наиболее подходящее по значению для проверки гипотезы из фактически имеющихся в таблице.

Пример 2. Имеется пять рядов данных, полученных в результате медико-биологических исследований, проверка которых не подтвердила, что закон распределения нормальный. Необходимо определить, средние значения каких выборок статистически значимо различаются.

На первом шаге строим ранги по каждой строке таблицы наблюдений и помещаем их в столбец H.

Затем находим суммы рангов по всем столбцам. Для этого в ячейку H16 помещаем формулу «=СУММ(H2:H14)=62».

Затем составляем таблицу абсолютных значений разницы между суммами рангов столбцов. Для этого в ячейке H19, I20, J21, K22 вводим формулы «=ABS($H$16-I$16)», «=ABS($I$16-J$16)», «=ABS($J$16-K$16)», «=ABS($K$16-L$16)». В остальные ячейки соответствующих строк размножаем формулы перетягиванием. В результате мы получаем таблицу программы Excel, в которой в 19-й строчке размещены абсолютные значения разницы между суммой рангов первой выборки и всех остальных, в 20-й – абсолютные значения разницы между суммой рангов второй выборки и всех остальных и т.д. (рис. 3.11)

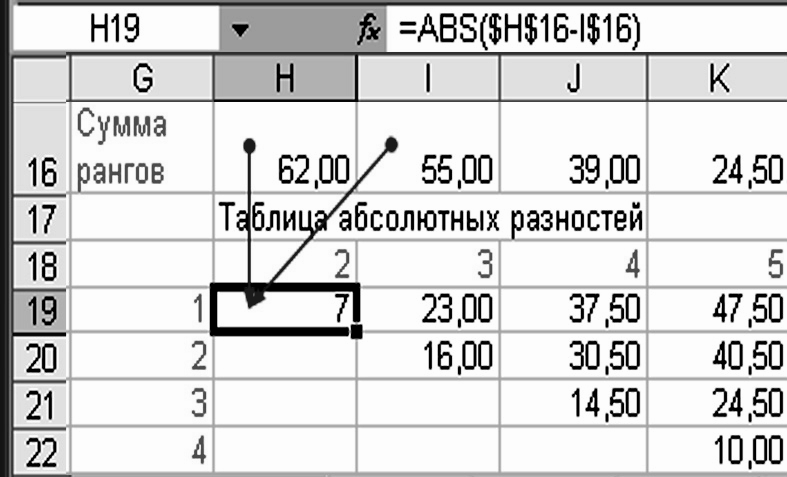
Рисунок 3.11 – Таблица программы Excel абсолютных разностей

Далее проверяем гипотезы о различии средних значений статистической выборки. Для этого из таблицы В.4 берем соответствующее значение для пяти выборок (k=5) и тринадцати наблюдений (n=13). =23. Этому критериальному значению соответствует уровень значимости 0,035. Видно, что больше значениябудет разница между первой и четвертой, первой и пятой, второй и четвертой, второй и пятой, третьей и пятой выборками. Это значит, что средние значения этих пар выборок статистически значимо различаются. Те пары, для которых абсолютное значение разницы меньше критериально, не различаются.

Для сравнения более чем двух независимых выборок используется H-тест по методу Крускала – Уоллиса. Этот тест является модификацией U-теста Манна – Уитни на случай для более двух независимых выборок. Он также базируется на общей ранговой последовательности значений всех выборок.

Назначение: проверка гипотезы о том, что несколько (k) выборок имеют одинаковое распределение и, следовательно, средние значения этих выборок равны между собой.

Нулевая гипотеза: все k-выборки имеют одинаковое распределение.

Альтернативная гипотеза: нулевая гипотеза неверна.

Пример 3. Необходимо протестировать три группы пациентов на предмет значимости различия показателя СОЭ при условии, что все случайные величины взаимно независимы.

Проверим, можно ли считать, что данные распределены по нормальному закону. Для этого в ячейках B16, C16, D16 помещаем вызовы функции NORMSAMP_1. Ответ во всех трех случаях отрицателен, поэтому мы вправе применять ранговый критерий.

Объединим все выборки в одну группу, которая занимает ячейки F3:F34. Затем для объединенной выборки все наблюдения заменяются рангами (рис. 3.12).

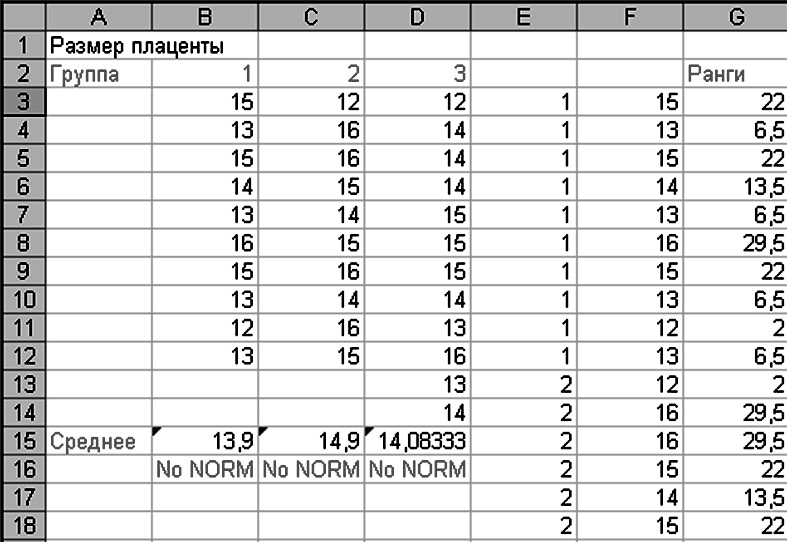
Рисунок 3.12 – Объединенная выборка и ранги значений выборки

На следующем шаге определяют критериальное значение Крускала – Уоллиса по формуле

, (3.6)

где N – общее количество наблюдений, определяемое как ;

– количество наблюдений в каждой выборке;

– сумма рангов по каждой выборке, определяемое как;

– рангj-го наблюдения в i-й выборке;

k – количество выборок.

Для этого находим сумму рангов для каждой выборки, рассчитываем квадраты сумм рангов и находим квадраты рангов, деленные на количество экспериментов (рис. 3.13).

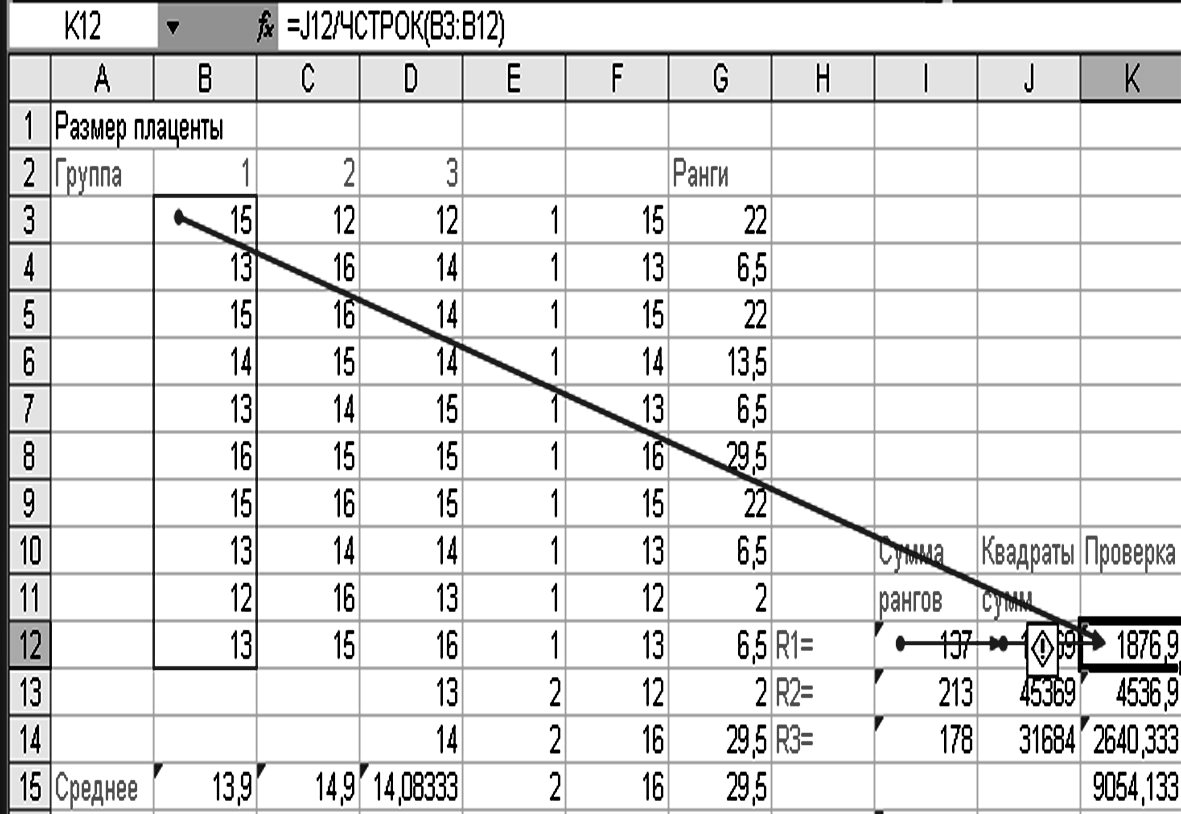
Рисунок 3.13 – Предварительная обработка исходных данных

Для использования в дальнейших расчетах в ячейку I16 помещаем значение N (общее количество наблюдений) «=ЧСТРОК(В3:В12)+ЧСТРОК(С3:С12)+ ЧСТРОК(D3:D12)=32». В ячейки I17 рассчитываем критериальное значение по формуле «=(12/(I16*(I16+1)))*K15-3*(I16+1)=3,887» (рис. 3.14).

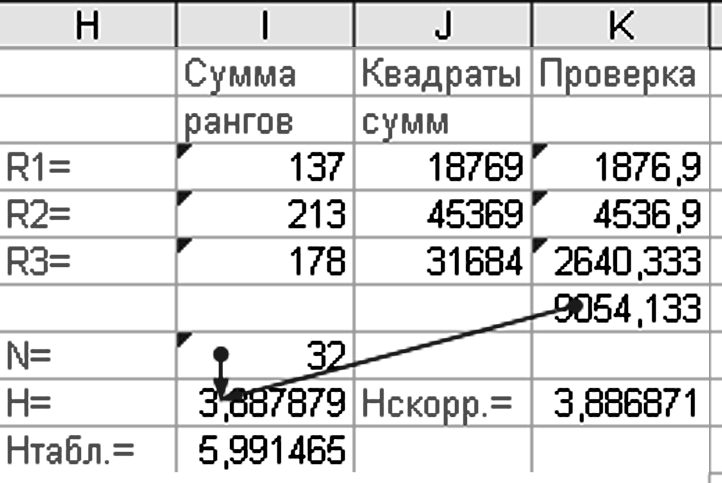
Рисунок 3.14 – Расчет критерия Крускула – Уоллиса

Если общее количество опытов больше 15, то в качестве критического используют значение счислом степеней свободы.

Так как в нашем случае количество опытов 32, для получения табличного значения можно воспользоваться процентной точкой распределения . Для этого в ячейкуI18 помещаем вызов функции «=ХИ2ОБР(0,05;3-1)=5,99». Здесь 3 – количество выборок, 0,05 – уровень значимости.

Выполняем сравнение расчетного значения критерия H с критическим (табличным) значением. Если расчетное значение критерия H больше критического, то нулевая гипотеза отклоняется и мы не можем считать, что средние значения равны между собой.

В нашем примере Н расчетное (3,887879) меньше Н табличного (5,99), следовательно, нулевая гипотеза принимается и мы можем считать, что средние значения этих выборок равны.

Если в столбце наблюдений имеются связки (одинаковые значения), то значение критерия корректируется по формуле

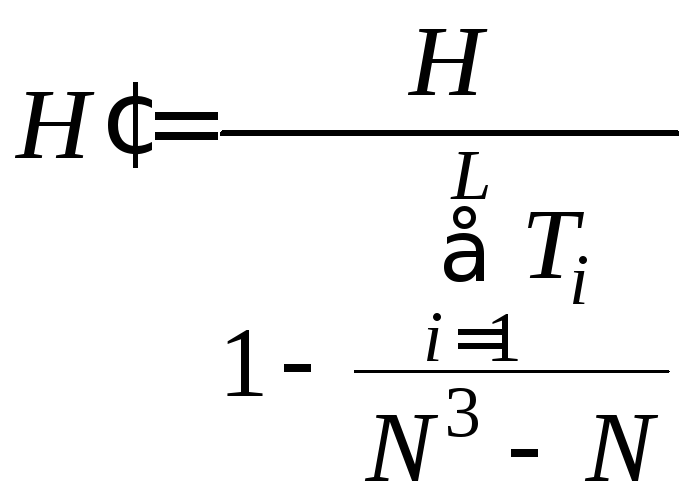, (3.7)

где L – количество связок;

T_i – количество совпадающих элементов в i-й связке.

В нашем примере много связок: 6 значений по 16; 9 по 15; 8 по 14; 7 по 13; 3 по 12. Таким образом L=5, а массив T={6, 9, 8, 7, 3} и скорректированное значение критерия (3.7) . При скорректированном значении наши выводы не меняются.

Для проверки принадлежности K-выборок к одной генеральной совокупности используют медианный критерий для нескольких выборок. С точки зрения исследователя – это проверка одновременного равенства медиан нескольких выборок.

Нулевая гипотеза: все совокупности, из которых получены выборки, имеют одинаковый закон распределения (следовательно, медианы одинаковы).

Предпосылки: все случайные величины взаимно независимы. Наблюдения, входящие в одну выборку, принадлежат к одной генеральной совокупности.

Вначале находим медиану объединенной выборки и после этого формируем таблицу, форма которой соответствует таблице 3.1.

Таблица 3.1 – Таблица для проверки медианного критерия

	Выборка				Всего
	1	2	…	К
Количество наблюдений, которые больше медианы			…
Количество наблюдений, которые меньше медианы			…
Всего			…

Вычисляют ожидаемое количество наблюдений для каждой клетки (при выполнении нулевой гипотезы). Для этого элемент строки «Всего» (соответствующий данной клетке) умножают на элемент столбца «Всего» (этой же клетки) и делят на общее количество наблюдений n. Затем вычисляют расчетное значение критерия по формуле

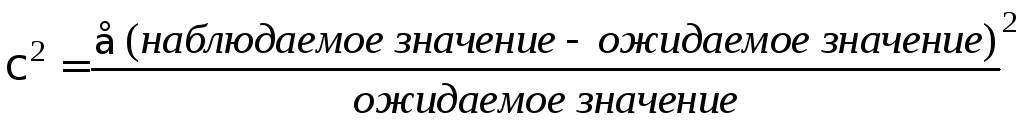. (3.8)

Сумма находится по всем 2К клеткам таблицы. Ожидаемое значение для первой строки (в которой находятся значения ) определяют по формуле

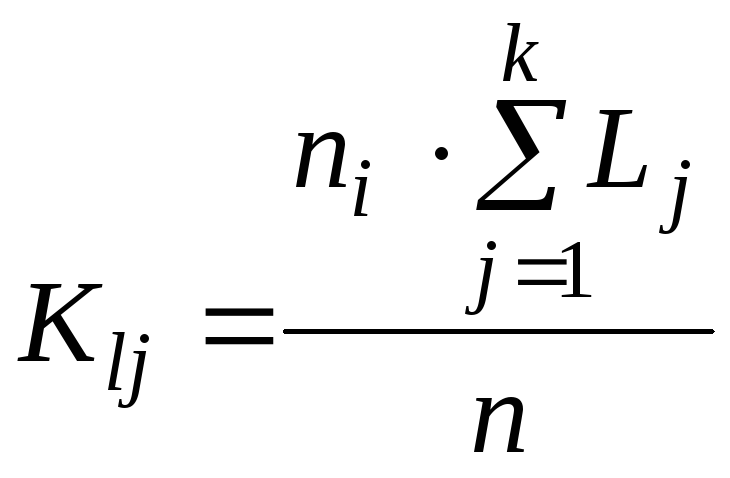. (3.9)

Для второй строчки (в которой находятся значения ) ожидаемое значение определяют по формуле

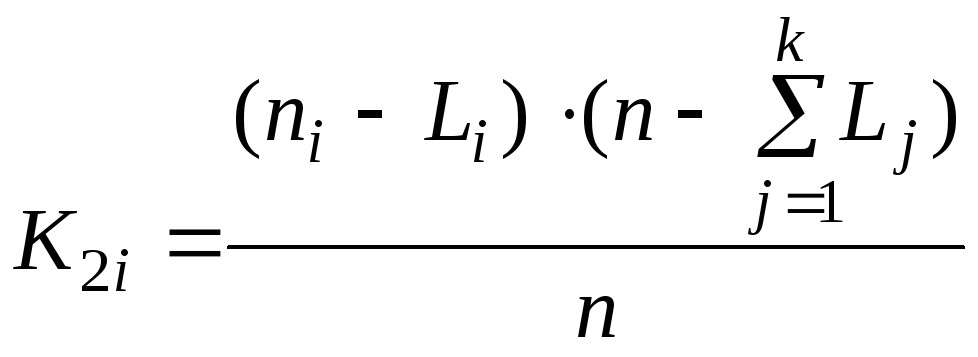. (3.10)

Если рассчитанное значение больше критического значения распределения , взятого с выбранным уровнем значимостиα и числом степеней свободы (К – 1), то гипотеза о равенстве медиан отвергается.

Пример 4. Есть данные о размере плаценты для трех выборок (рис. 3.12). Для проверки гипотезы о равенстве медиан этих выборок необходимо выполнить следующие действия.

Определяем медианы для всех трех выборок. Для этого в ячейки В17, С17, D17 помещаем формулу «=МЕДИАНА(B3:B13)», «=МЕДИАНА(C3:C13)», «=МЕДИАНА(D3:D13)» соответственно. Далее в столбцах E, F, G помещаем единицы, если значение наблюдения больше медианы, в противном случае – нули. Это можно сделать с помощью формулы «=ЕСЛИ($B3>$B$17;1;0)», «=ЕСЛИ($C3>$C$17;1;0)», «=ЕСЛИ($D3>$D$17;1;0)» соответственно, которые входят в ячейки E3, F3 и G3, а затем размножаем на все соответствующие столбцы (рис. 3.15).

Рисунок 3.15 – Определение медиан для всех выборок

Формируем необходимую нам таблицу сопряженности для проверки медианного критерия (табл. 3.2).

Таблица 3.2 – Таблица сопряженности для проверки медианного критерия

Строки/столбцы	Выборка 1(Н)	Выборка 2(I)	Выборка 3(J)	Всего (К)
Количество наблюдений, которые больше медианы (18)	= СУММ (Е3:Е12)	= СУММ (F3:F12)	= СУММ (G3:G14)	= СУММ (H18:J18)
Количество наблюдений, которые меньше медианы (19)	=Н20-Н18	=I20-I18	=J20-J18	= СУММ (H19:J19)
Всего (20)	=ЧСТРОК(В3:В12)	=ЧСТРОК(С3:С12)	=ЧСТРОК(D3:D14)	= СУММ (H20:J20)

Формируем таблицу из расчетных ожидаемых значений (табл. 3.3, рис. 3.16).

Таблица 3.3 – Расчетные ожидаемые значения

Столбец	L	M	N
Строка	1	2	3
18	=H18*$K$18/$K$20	=I18*$K$18/$K$20	=J18*$K$18/$K$20
19	=H19*$K$19/$K$20	=I19*$K$19/$K$20	=J19*$K$19/$K$20
20	=(H18-L18)*(H18-L18)/L18	=(I18-M18)*(I18-M18)/M18	=(J18-N18)*(J18-N18)/N18

Р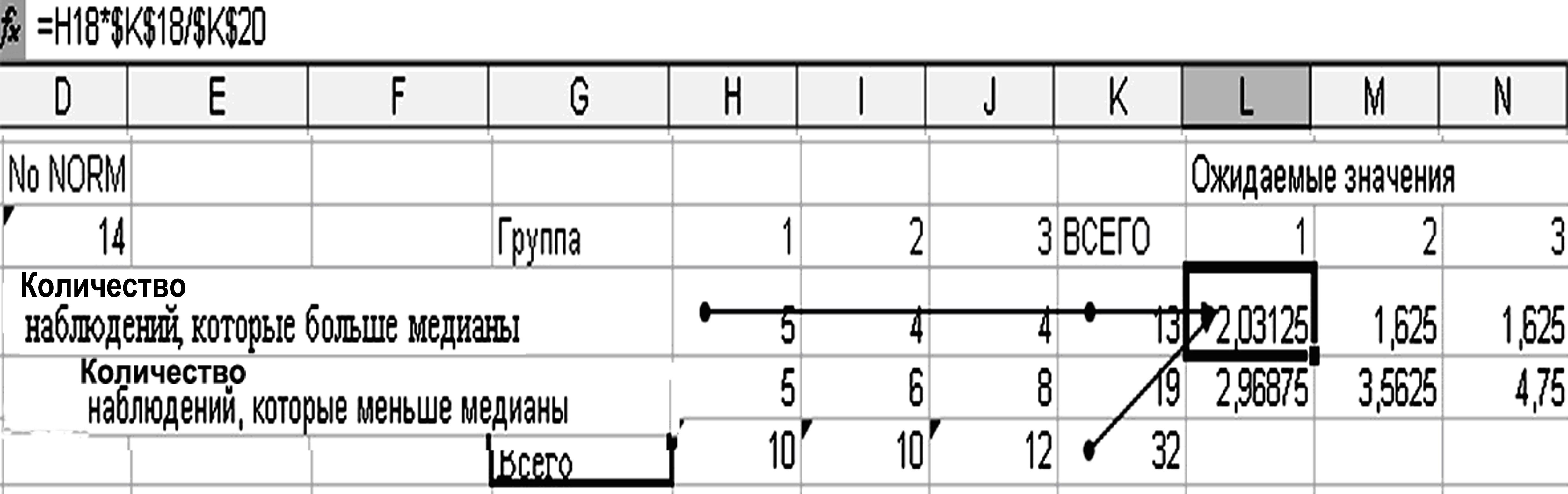исунок 3.16 – Расчетные ожидаемые значения

Рассчитываем критериальное значение по формуле «=СУММ(L22:N22)», введенной в ячейку L24. С помощью функции «=ХИ2ОБР(0,05; 3-1)= 5,99» вычисляем табличное значение для сравнения с критериальным. Поскольку критериальное значение больше табличного, то нулевая гипотеза отвергается.

3.3 Описание лабораторной установки

Для проведения лабораторной работы используется персональная ЭВМ типа IBM PC/ATX, которая позволяет автоматизировать процесс распознавания патологических процессов с использованием критериев множественных сравнений при помощи программного средства Microsoft Excel.

Основные характеристики установки:

• процессор – Intel Celeron с частотой не ниже 1000 MGz;

• ОЗУ – не меньше 256 Mb.

Программное средство работает в ОС Windows 2000 и больше, занимает 135 Mb дискового пространства. Для нормальной работы необходима графическая подсистема ЭВМ (дисплей и видеокарта), которая может отображать 1024х768 пикселя при 32-битной цветовой палитре.

3.4 Порядок выполнения работы и методические указания по ее выполнению

1. Запустить программу Excel, выполнив команды «Пуск» ► «Программы» ► «Microsoft Excel».

2. Создать чистую рабочую книгу, выполнив команды «Файл» ► «Создать» ► «Чистая книга».

3. Решить задачу 1 (приложение В):

а) заполнить «Лист 1» рабочей книги исходными данными, состоящими из пяти выборок, согласно своего варианта (табл. В.1) как показано на рисунке 3.1;

б) определить среднее арифметическое значение для каждой из групп, используя функцию ExcelСРЗНАЧ;

в) проверить распределены ли выборки по нормальному закону с помощью функции NORMSAMP_1.

- Для этого необходимо выполнить команды «Файл» ► «Открыть». В открывшемся диалоговом окне «Открытие документа» в строке «Папка» выбрать папку «Студент».

- Выбрать файл Excel «Метод_Шеффе. xls». Перейти в свою рабочую книгу и вызвать мастер функций Excel .

- В открывшемся диалоговом окне «Мастер функций» выбрать функцию «Метод_Шеффе.xls!NORMSAMP_1» и нажать «ОК».

- В появившемся диалоговом окне «Аргумент функции» в строку «R_1» ввести диапазон ячеек, содержащих выборку проверяемых значений и нажать «ОК». Повторить описанные действия для всех групп значений;

г) определить количество наблюдений в каждой группе, используя функцию Excel ЧСТРОК;

д) определить общее количество наблюдений n, используя функцию Excel СУММ;

е) с помощью функции Excel ЧИСЛСТОЛБ определить количество выборок k;

ж) рассчитать значение внутригрупповой дисперсии .

- Сформировать вспомогательную матрицу дисперсий, рассчитав в свободной ячейке формулу .

- Размножить формулу на все ячейки исследуемого диапазона (рис. 3.3).

- Определить значение внутригрупповой дисперсии по (3.3), используя функцию СУММ (рис. 3.4);

з) построить матрицу коэффициентов С_i.

- Сформировать столбец заголовка всех комбинаций средних значений исследуемых групп, задав имена комбинаций как 1&2, 1&3, 1&4, ..., 1&n, 2&3, 2&4, ..., 2&n, ..., k&n.

- Выполнить попарно сравнение всех средних значений. Для средних, которые сравниваются, ставить 1 и -1, соответственно, для всех остальных – 0 (рис. 3.5).

- Определить константы () (рис. 3.6) для всех групп исследования;

и) рассчитать критериальное значение Шеффе по (3.2).

- Для этого необходимо, используя функцию СУММ, определить столбец контрастов для всех пар средних (рис. 3.17).

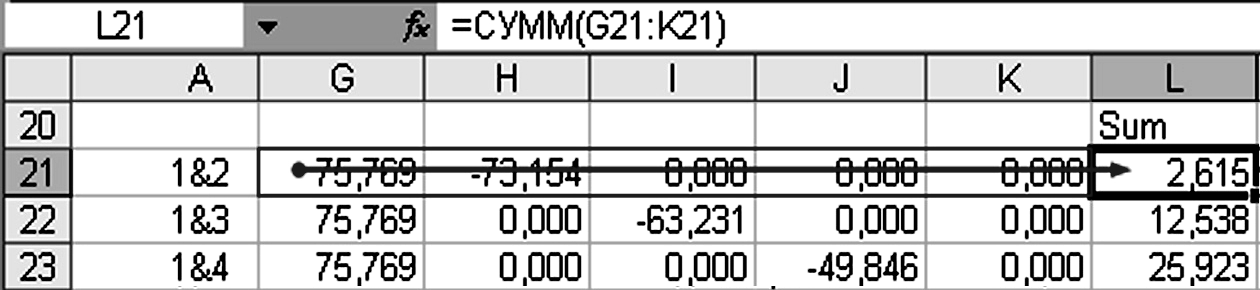
Рисунок 3.17 – Определение контрастов для всех пар средних

- Определить столбец квадратов контрастов 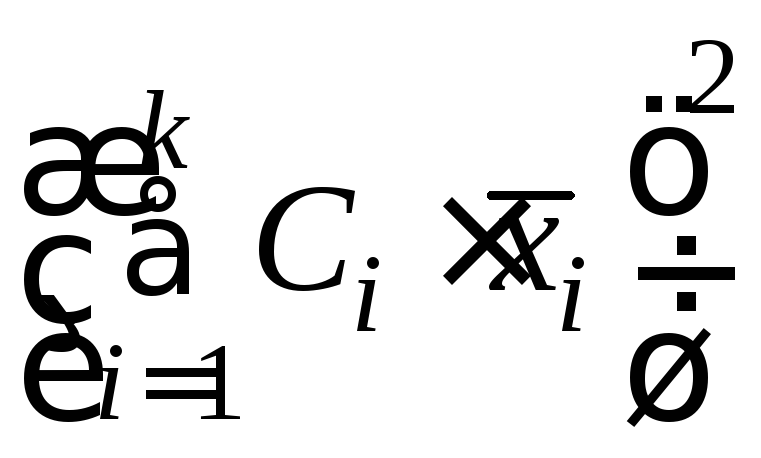(рис. 3.18).

Рисунок 3.18 – Определение квадрата контрастов

- Определить столбец критериальных значений Шеффе (рис 3.7);

к) проверить гипотезу о равенстве средних соответствующих групп выборок.

- Рассчитать критическое значение F-распределения (рис. 3.8), используя функциюExcel FРАСПОБР(α; k-1; n-k), где α=0,05.

- Сравнить критериальное значение Шеффе для каждой сравниваемой пары с критическим значением F-распределения, используя логическую функцию Excel «=ЕСЛИ (S<; ”Одинаковы“; ”Различны“)» (рис. 3.9);

л) провести распределение средних значений по однородным группам.

- Для этого необходимо сформировать таблицу разницы между соседними средними (табл. В.2, рис. 3.19).

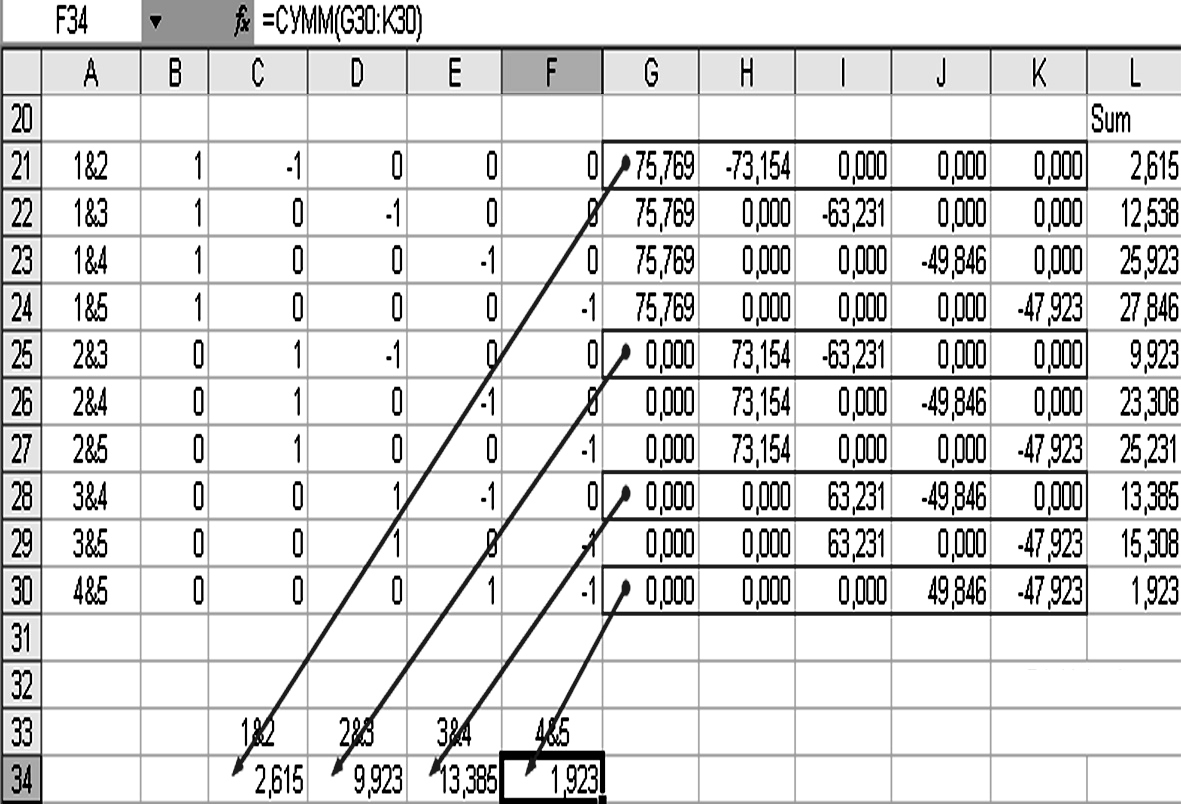
Рисунок 3.19 – Формирование таблицы разницы между соседними средними

- Рассчитать значение LSD по (3.4), используя функцию Excel СТЬЮДРАСПОБР (рис. 3.10);

м) сравнить полученные значения разницы средних значений соседних групп выборок с рассчитанным значением LSD, используя логическую функцию Excel «=ЕСЛИ (<LSD; ”Одна группа“; ”Разные группы“)».

4. Решить задачу 2 (приложение В):

а) заполнить «Лист 2» рабочей книги исходными данными, состоящими из четырех выборок, согласно своего варианта (табл. В.3) как показано на рисунке 3.1;

б) определить среднее арифметическое значение для каждой из групп, используя функцию ExcelСРЗНАЧ;

в) проверить, распределены ли выборки по нормальному закону с помощью функции NORMSAMP_1;

г) сформировать таблицу рангов по каждой строке исходных данных, как показано на рисунке 3.20;

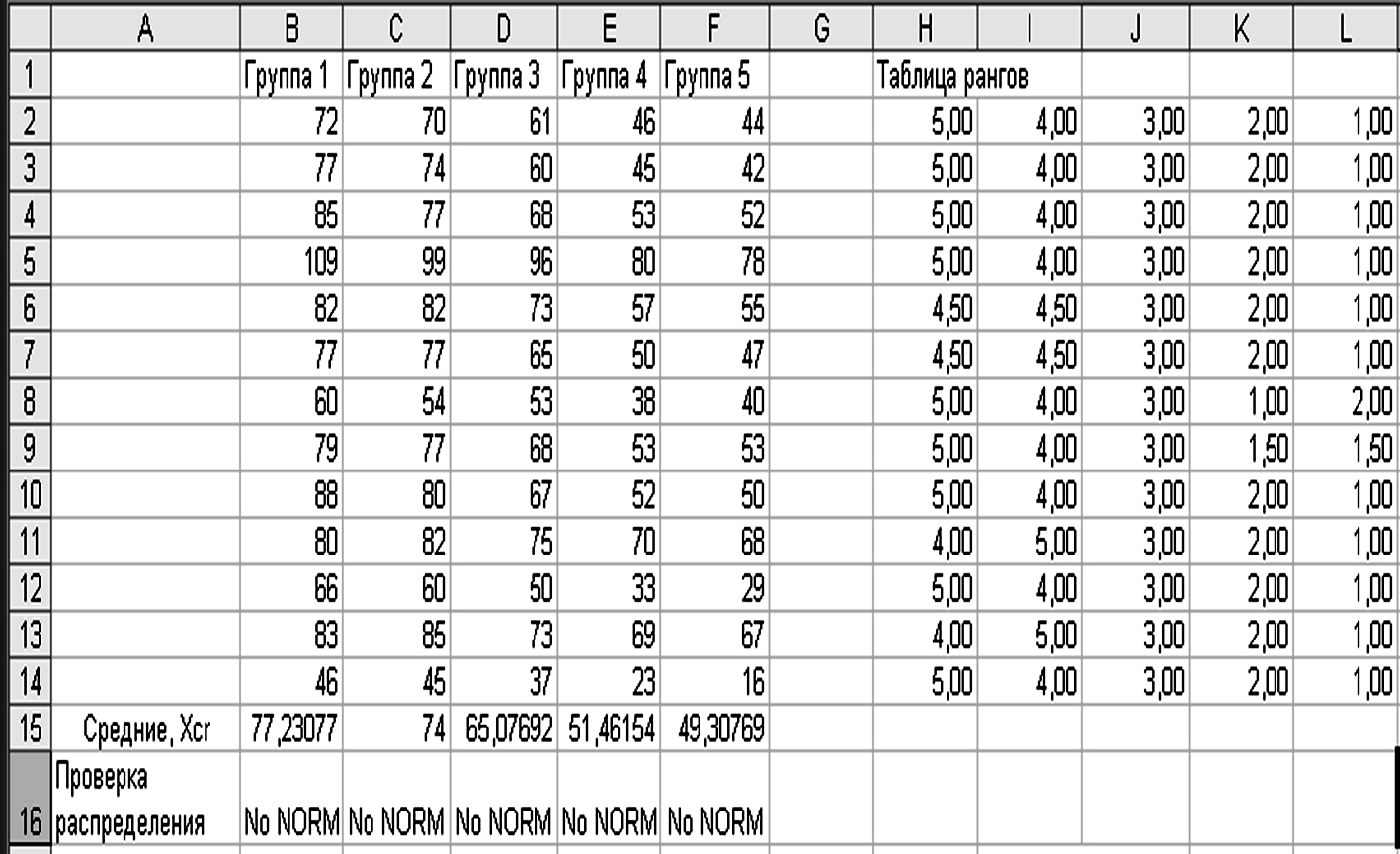
Рисунок 3.20 – Таблица рангов значений каждого наблюдения

д) определить суммы рангов по всем столбцам, используя функцию СУММ (рис. 3.21);

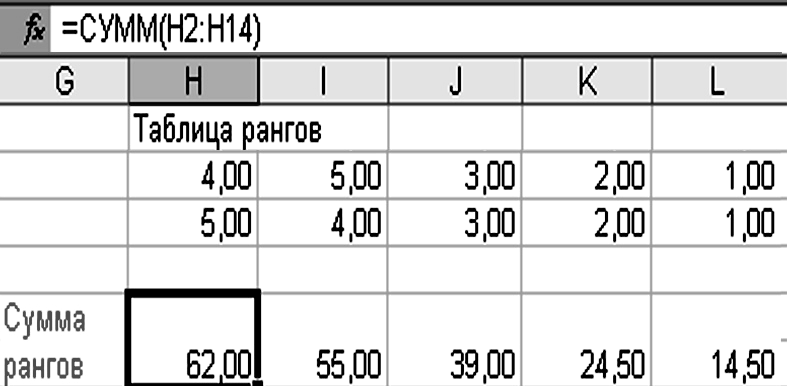
Рисунок 3.21 – Расчет суммы рангов

е) составить таблицу абсолютных разностей между суммами рангов столбцов, используя функцию ABS (рис. 3.11);

ж) определить статистическую значимость различий средних значений в четырех выборках.

- Для этого необходимо определить по таблице В.4 значение .

- Определить уровень значимости α.

- Сравнить полученное значение с каждым значением таблицы абсолютных разностей.

5. Решить задачу 2 (приложение Б) с помощью пакета SPSS:

а) поместить исходные данные в поле исходных переменных пакета SPSS;

б) выбрать в меню «Nonparametric Tests» ► «К Related Samples». В появившемся окне «Test for Several Related Samples» установить флажок на тесте Фридмана;

в) перенести по очереди переменные в поле тестируемых переменных, нажать «ОК»;

г) проанализировать полученные результаты. Если показатель получится значимым, произвести попарно тестирование при помощи критерия Вилкоксона.

- Для этого выполнить команду «Nonparametric Tests» ► «2 Related Samples».

- В поле тестируемых переменных выбрать необходимые пары и перенести в поле для спаренных переменных.

- Запустить тест Вилкоксона на исполнение нажатием клавиши «ОК».

- Провести анализ полученных результатов. Если величина р =0,000, это свидетельствует об очень значимой разнице.

6. Решить задачу 3 (приложение В) с помощью пакета Excel:

a) заполнить «Лист 3» рабочей книги исходными данными согласно своего варианта (табл. В.5);

б) определить средние значения для каждой экспериментальной выборки, используя функцию Excel СРЗНАЧ;

в) определить, можно ли считать, что данные распределены по нормальному закону, используя функцию NORMSAMP_1;

г) объединить все выборки в одну;

д) для объединенной выборки определить ранг каждого значения;

е) определить сумму рангов для каждой выборки, используя функцию Excel СУММ;

ж) рассчитать квадраты сумм рангов;

з) определить значения квадратов рангов, деленных на количество экспериментов с использованием функции ЧСТРОК;

и) определить общее количество наблюдений;

к) определить правильность расчетов по рангам;

л) рассчитать критериальное значение H по (3.6);

м) определить процентную точку (критическое значение Крускала – Уоллиса);

н) сравнить полученное значение H и критическое значение Крускала – Уоллиса;

о) определить наличие связок в столбце наблюдений. Если такие имеются, то необходимо скорректировать критериальное значение H по (3.7).

7. Решить задачу 3 (приложение В) с помощью пакета SPSS:

а) поместить значения объединенной выборки исследуемых переменных (п. 6.г) в поле исходных переменных пакета SPSS. Напротив значений исследуемых переменных ввести коды каждого значения (1 – для первой группы, 2 – для второй, 3 – для третьей и т.д.);

б) выбрать в меню «Nonparametric Tests» ► «К Independent Samples». В появившемся окне «Test for Serveral Independent Samples» установить флажок на тесте Крускала – Уоллиса Н;

в) перенести переменную значений объединенной выборки в поле тестируемых переменных, а групповую переменную в поле групповых переменных и нажать «ОК». После щелчка на кнопке «Define Groups» внести значения 1 и 3 для минимального и максимального значения переменной соответственно и нажать «ОК»;

г) проанализировать полученные результаты.

8. Решить задачу 4 (приложение В) с помощью пакета Excel:

а) определить медианы для всех выборок;

б) закодировать исходные данные. Для этого с помощью функции ЕСЛИ в новых столбцах поместить единицы, если значение наблюдения больше медианы, в противном случае – нули (рис. 3.15);

в) сформировать таблицу сопряженности для проверки медианного критерия (табл. 3.2);

г) сформировать таблицу из расчетных ожидаемых значений (табл. 3.3, рис. 3.16);

д) рассчитать критериальное значение, используя функцию СУММ;

е) вычислить табличное значение медианного критерия, используя функцию ХИ2ОБР;

ж) сравнить рассчитанное и табличное значения медианного критерия.

3.5 Содержание отчета

Отчет по лабораторной работе должен содержать: цель работы, исходные данные и результаты решения задач с оценкой полученных значений, распечатку полученных результатов, выводы.

3.6 Контрольные вопросы и задания

1. Назовите особенности применения метода Шефе.

2. В каких случаях используются непараметрические критерии?

3. Приведите пример применения критерия рангов Фридмана, используя программный продукт SPSS.

4.В каких случаях используется H-тест по методу Крускала и Уоллиса и на чем он базируется?

5. Приведите основные этапы проверки принадлежности K-выборок к одной генеральной совокупности, используя медианный критерий для нескольких выборок.