Параллельное соединение элементов в цепи синусоидального тока

В электрических цепях переменного тока имеются цепи с параллельным соединением потребителей электроэнергии, при котором все потребители находятся под одним и тем же напряжением. При этом на ток в цепи каждого из потребителей не влияет их число. Значение тока в каждом из них определяется только значениями соответствующих сопротивлений и значением подводимого напряжения. Наличие на различных участках цепей переменного тока как активных, так и реактивных элементов приводит к тому, что сопротивление этих участков имеет комплексный характер. В качестве примера рассмотрим цепь, представленную на рис. 8, а. Данная цепь состоит из двух параллельно соединенных ветвей, характер сопротивлений которых различен. Эта схема может рассматриваться как схема замещения реальной цепи, содержащей неидеальные катушку индуктивности и конденсатор. СопротивлениеR₁ учитывает наличие потерь в витках обмотки катушки, аR₂ – потери энергии в диэлектрике конденсатора.

Анализ работы данной цепи проведем на основе построения векторной диаграммы токов и напряжений. Вначале рассмотрим графоаналитический метод расчета. Определим действующие значения токов ветвей, используя закон Ома:

.

Данные соотношения позволяют определить длины векторов токов на комплексной плоскости. Для построения вектора тока на комплексной плоскости необходимо, помимо длины вектора, знать его ориентацию относительно вектора напряжения на соответствующем участке цепи (угол сдвига фаз). Углы сдвига фаз ₁и₂ между напряжением и токами ветвей могут быть определены из следующих соотношений:

.

Примем начальную фазу напряжения uна входе рассматриваемой цепи равной нулю, что соответствует ориентации вектора напряжения, совпадающей с положительным направлением оси вещественных чисел (рис. 8,б). Рассчитанные выше углы сдвига фаз₁и₂ представляют собой углы между соответствующими векторами токов () и напряженияна комплексной плоскости. Причем, при активно-индуктивном характере сопротивления (в данной схеме первая ветвь) напряжение опережает ток на угол₁, а при активно-емкостном сопротивлении (вторая ветвь) – напротив, напряжение отстает по фазе от тока на угол₂. Вектор общего тока цепи в соответствии с первым законом Кирхгофа равен геометрической сумме векторов токов ветвей:

.

Действующее значение общего тока Iопределяется графически по векторной диаграмме как длина вектора.

Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности. Более эффективным является использование комплексного метода расчета с использованием проводимостей. Под комплексной проводимостью участка цепи (ветви) Yпонимают величину, обратную комплексному сопротивлению этого участкаZ:

Y=1/Z = G – jB = Ye^–j

Единица измерения проводимости – (Ом^-1) или (См) (читается: сименс). Вещественная часть комплексной проводимостиG называется активной проводимостью участка цепи, а мнимая часть комплексной проводимостиB называется реактивной (индуктивной или емкостной) проводимостью. Учитывая что комплексное сопротивление участка цепи в общем виде может быть представлено в видеZ = R+jX, запишем выражение для комплексной проводимости через активную и реактивную составляющие комплексного сопротивления участка цепи:

;

.

Если комплексное сопротивление участка цепи имеет индуктивный характер, то B> 0, если же характер комплексного сопротивления емкостный, тоB< 0. Для рассматриваемой схемы проводимости ветвей имеют вид

;

.

Таким образом, выражения для активных (G₁иG₂) и реактивных (B₁иB₂) проводимостей ветвей рассматриваемой цепи имеют вид

;

.

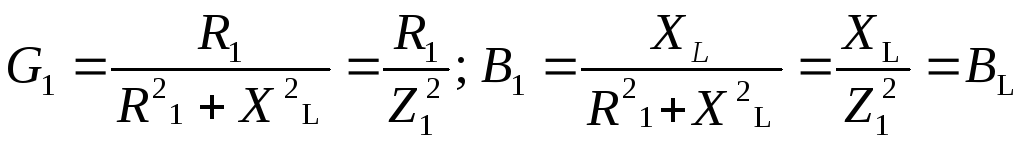Здесь через Z₁иZ₂обозначены модули комплексных сопротивлений ветвей. Токи ветвей на основе закона Ома могут быть представлены в виде

;

.

Анализ полученных выражений показывает, что ток любого участка цепи может быть представлен в виде суммы двух составляющих. Векторы активных составляющих токов ветвей () параллельны вектору напряженияU, тогда как векторы реактивных составляющих токов ветвей () ему перпендикулярны. Представление токов ветвей в виде суммы двух составляющих является удобным математическим приемом, непосредственному измерению они недоступны. На векторной диаграмме (см. рис. 8,б) реактивная составляющая тока первой ветвиотстает по фазе от вектора напряжения на угол 90, а реактивная составляющая тока второй ветвиопережает вектор напряжения на такой же угол.

На основании первого закона Кирхгофа, составленного для точки разветвления, получим выражение для общего тока Iв неразветвленном участке цепи:

.

Из этого выражения следует, что комплексная проводимость электрической цепи при параллельном соединении сопротивлений оказывается равной сумме комплексных проводимостей соответствующих параллельных ветвей:

.

Отсюда в общем случае для произвольного числа параллельных ветвей активная проводимость электрической цепи оказывается равной сумме активных проводимостей всех параллельных ветвей, а реактивная проводимость цепи – равной алгебраическойсумме реактивных проводимостей всех параллельных ветвей, входящих в данную электрическую цепь.

а)б)в)

Рис. 8

Модуль полной проводимости цепи определяется из выражения

Y = .

Полная проводимость цепи в то же время является и величиной, обратной ее полному сопротивлению Y= 1/Z.

Из треугольника токов, представленного на векторной диаграмме (см. рис. 8, б), можно получить треугольник проводимостей для рассматриваемой цепи, разделив стороны этого треугольника на комплексное напряжение(см. рис. 8,в).

Из треугольника проводимостей следует, что cos=G/Y, а sin=B/Y= (B_LB_C)/Y_.

С учетом этого полная, активная и реактивная мощности цепи могут быть определены через соответствующие проводимости:

S = UI = U ²Y; P = UIcos = U² G ; Q = UIsin = U² B.