1.3 Ускорение точки

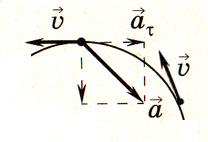
Среднее ускорение  

характеризует изменение вектора скорости за малый промежуток времени  Δt . Ускорение точки в данный момент времени

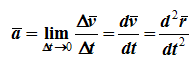
Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

15. Определение скорости и ускорения при координатном способе задания движения точки.

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

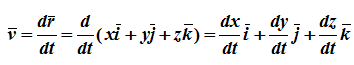
Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

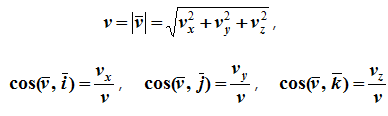
Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

16. Тангенциальное и нормальное ускорение точки.

Нормальное и тангенциальное ускорение
При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.

Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения

17. Относительное, переносное и абсолютное движения. Теорема о сложении скоростей.

    Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3) 

                                        a_a = a_r  ⊕   a_e  ⊕  a_C   .

Рис. 3

    Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r  направлено вдоль этой прямой и определяется выражением

    Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

  a_e = a_e^вр  ⊕  a_e^цс            ,

где  a_e^вр= ε⋅ OM  - вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;

       a_e^цс= ω²⋅ OM - центростремительное ускорение точки M, направленное к центру диска.

    Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e  ⊗  ν_r          , где  ω_e - переносная угловая скорость,  ν_r  - относительная скорость точки.

    Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

    Величина ускорения Кориолиса определяется выражением

         a_C = 2 ω_e  ν_r  sinα      ,

где  α  – угол между векторами ω_e  и ν_r  .

    Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

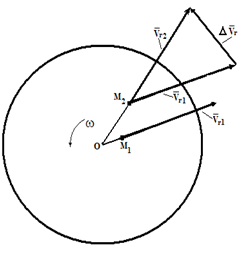
Рис. 4

    Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_{r 1} . За промежуток времени Δt точка M переместится в положение M₂ , при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r . Отношение  Δν_r / Δt определяет среднее ускорение точки за промежуток времени Δt . Предел отношения  Δν_r / Δt при  Δt→ 0 есть производная  dν_r /dt , как производная от вектора постоянного по величине.

    Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями ν_e1= ω ⊗ OM₁  и  ν_e2= ω ⊗ OM₂ . Тогда приращение вектора  ν_e за счет относительного движения будет равно 

 Δν_e = ω  ⊗ OM₂ - ω ⊗  OM₁ = ω  ⊗ (OM₂ - OM₁) = ω ⊗  ν_r⋅ Δt 

    Отношение Δν_e / Δt в пределе при  Δt→ 0 дает производную dν_e / d t = ω ⊗  ν_r  . Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Рис. 5

    Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

    Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов: