КОНТРОЛ-САМОСТ задания по математике

Найти Z = A(C − 3A).

4) Даны точки А (4,3,1), B (2,0,9), C (1,0,6), D (9,1,2).

а) Составить уравнение высоты, опущенной из (.) D на плоскость АВС. б) Найти площадь треугольника АВС.

5) Даны точки A (5,–1), B (3,4), уравнение прямой Р: 3x – 2y + 15 = 0. Определить угол между прямыми и координаты (.) D – точки пересечения прямых. Сделать чертеж.

6) Привести уравнение кривой 2x2 + 2y2 + 2x − 2y −1= 0 к каноническому виду. Сделать чертеж, определить координаты вершин и фокусов.

Вариант 29 1) Решить систему по правилу Крамера, матричным способом и

методом Гаусса:

Найти Z = (C − 3A)A.

4) Даны точки А (4,3,1), B (2,0,9), C (1,0,6) и прямая x −1= y −1= z + 5 .

5 3 1

а) Найти площадь треугольника АВС.

б) Будет ли данная прямая параллельна плоскости АВС?

31

5) Даны точки B (3,4), C (6,8), уравнение прямой Р: 3x – 2y + 1 = 0. Определить угол между прямыми и координаты (.) D – точки пересечения прямых. Сделать чертеж.

6) Привести уравнение кривой − 64x2 +16y2 + 8y − 63 = 0 к каноническому виду. Сделать чертеж, определить координаты вершин и фокусов.

Вариант 30

1)Решить систему по правилу Крамера, матричным способом и

4)Даны точки А (4,3,1), B (2,0,9), С (1,0,6). а) Составить уравнение плоскости АВС. б) Составить уравнения прямых АВ и ВС.

5)Даны точки A (5,–1), B (3,4), C (6,8). Составить уравнения прямых АВ

иАС, найти угол между ними. Сделать чертеж.

6) Привести уравнение кривой 4x2 +16y2 − 4x + 64y + 49 = 0 к каноническому виду. Сделать чертеж, указать координаты вершин и фокусов.

Вариант 31 1) Решить систему по правилу Крамера, матричным способом и

методом Гаусса:

32

Найти Z = A2 + A.

4)Даны вершины треугольника А (4,3,1), B (2,0,9), C (1,0,6). Составить уравнение высоты ВК в треугольнике АВС.

5)Даны точки A (5,–1), B (3,4), C (6,8) – соседние вершины параллелограмма. Составить уравнения диагоналей параллелограмма, найти точку их пересечения. Сделать чертеж.

6) Привести уравнение кривой 16x2 − 4y2 − 4y − 65 = 0 к каноническому виду. Сделать чертеж, определить координаты вершин и фокусов.

Вариант 32 1) Решить систему по правилу Крамера, матричным способом и

Найти Z = B2 + A.

4)Даны точки А (4,3,1), B (2,0,9), C (1,0,6). Составить уравнение плоскости Р, проходящей через прямую АС перпендикулярно плоскости АВС.

5)Даны вершина прямоугольного треугольника A (5,–5), уравнения двух его сторон:

Р: 3x – 2y + 1 = 0, P1: 5x + y – 20 = 0.

Найти координаты вершин треугольника. Сделать чертеж.

33

6) Привести уравнение кривой x2 − y2 +10x + 26 = 0 к каноническому виду. Сделать чертеж, определить координаты вершин и фокусов.

4. Пределы

Решение. Подставляя предельное значение x = 1 в выражение, выясняем

0

наличие неопределенности вида , это означает, что именно выражение

0

(x −1) «мешает» разрешению предела. Выделим в числителе и знаменателе дроби именно этот множитель (x −1) (или разложим числитель и знаменатель на простые множители) и сократим его. Неопределенность устранена.

x→0 2 − 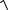x2 + x + 4

Решение. Подставляя предельное значение x = 0 в выражение предела,

0

выясняем наличие неопределенности вида . Но данный предел содержит

0

иррациональность.

Поэтому решение состоит из следующих шагов:

–избавиться от иррациональности;

–в полученном рациональном выражении разложить числитель и знаменатель на простые множители;

–избавиться от неопределенности и разрешить предел.

Чтобы избавиться от иррациональности, необходимо домножить числитель и знаменатель на сопряженный знаменателю множитель (2 + 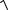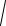x2 + x + 4), для этого затем используем в знаменателе формулу a2 − b2 = (a + b)(a − b).

34

выясняем наличие неопределенности вида 1∞ . Для решения необходимо использовать знание второго замечательного предела и эквивалентность бесконечно малых: tgx ~ x (тангенс бесконечно малого аргумента ведет себя аналогично своему аргументу).

В квадратных скобках отделим второй замечательный предел, затем переходим к пределу в показателе.

3x

Пример 7. Вычислить предел LIM(1− 2LN2 x)(x−1)2 .

x→1

35

Решение. Подставляя предельное значение x = 1 в выражение предела, выясняем наличие неопределенности вида (1∞ ).

Обратите внимание! Прежде чем применять замечательные пределы необходимо сделать замену переменной x −1= y: тогда при x → 1 также y → 0

В квадратных скобках выделен второй замечательный предел, который равен e−2.

Использована эквивалентность бесконечно малых: LN(1+ y) ~ y при

y→ 0.

4.1.Непрерывность функции, точки разрыва

Утверждение. Функция f (x) будет непрерывной в точке x = a , если функция определена в этой точке и существуют конечные пределы

Если нарушено хотя бы одно из условий, то функция терпит в точке x = a разрыв, а именно,

разрыв I рода:

при LIM f (x) = LIM f (x) ≠ f (a) – это точка устранимого разрыва,

x→a−0 x→a+0

разрыв II рода:

если хотя бы один из пределов не существует либо равен бесконечности – это неустранимый разрыв.

Определение. Функция называется непрерывной на отрезке [a,b], если непрерывна в каждой точке отрезка.

Пример 8. Исследовать непрерывность функции

36

x2 + x +1,при x ≤ 0, f (x) = 2 + LN x,при0 < x ≤ 5,

2x +1,при x > 5

Решение. При x ≤ 0 функция задана в виде многочлена и непрерывна в интервале. В двух других интервалах функция также определена как непрерывная. Точками разрыва могут быть только точки границ интервалов: x1 = 0, x2 = 5.

Рассмотрим x1 = 0.

Пределы слева и справа конечны, но не равны между собой – функция терпит в точке x2 = 5 скачок – разрыв I рода.

Ответ: функция непрерывна в

1

Пример 9. Определить непрерывность функции f (x) = ex−1. Решение. Единственная точка, подозрительная на разрыв x0 = 1.

Предел справа равен бесконечности, а это значит, что в точке x0 = 1

функция терпит неустранимый разрыв II рода.

Пример наглядно показывает, как важно учитывать знак выражения.

37

Ответ: функция непрерывна в (−∞,1) (1,+∞), в точке x0 = 1 имеет разрыв II рода.

Задача № 3. Вычислить предел от дробно-рациональной функции.

38

3x2 + 2x − 5

7x2 + 2x − 9

27)LIM x3 + 3x2 − x − 3 x→1

4.2.Самостоятельная работа. Вычислить пределы (5 заданий на один

вариант).

39