
- •В.С. Васильева, с.В. Коровина, л.В. Марченко дискретная математика
- •Васильева, в.С.
- •Введение
- •1. Элементы теории множеств
- •1.1. Основные понятия теории множеств. Способы задания множеств
- •1.2. Операции над множествами
- •1.3. Диаграммы Эйлера – Венна
- •1.4. Свойства операций над множествами
- •1.5. Декартово произведение множеств
- •1.6. Бинарные отношения. Свойства бинарных отношений
- •1.7. Функция
- •2. Элементы математической логики
- •2.1. Математическая логика как наука
- •2.2. Высказывания. Логические операции и их основные свойства
- •Логические операции
- •Новые логические операции
- •2.3. Способы решения логических задач
- •2.4. Булевы функции. Свойства элементарных булевых функций
- •2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций
- •2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •3. Элементы теории графов
- •3.1. Основные понятия теории графов
- •3.2. Способы задания графов
- •3.3. Связность графов
- •4. Элементы комбинаторики
- •4.1. Перестановки, размещения и их количество
- •4.2. Сочетания и их свойства
- •4.3. Выборки с повторением
- •5. Индивидуальные задания
- •Заключение
- •Библиографический список
- •Оглавление
1.5. Декартово произведение множеств
Пусть
даны два произвольных непустых множества
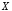 и
и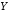 ,
элементы которых мы будем обозначать
,
элементы которых мы будем обозначать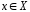 ,
,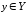 .
.
Определение.
Прямым
произведением
(или декартовым
произведением)
двух непустых множеств
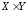 называется множество упорядоченных
пар
называется множество упорядоченных
пар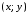 ,
где
,
где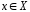 ,
, .
Упорядоченность пары означает, что если
мы будет рассматривать декартово
произведение
.
Упорядоченность пары означает, что если
мы будет рассматривать декартово
произведение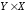 ,
то соответствующая пара будет иметь
вид
,
то соответствующая пара будет иметь
вид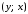 ,
где
,
где ,
,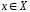 .
.
В
частности, декартово произведение
множества действительных чисел на себя
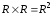 представляет собой множество всевозможных
упорядоченных пар действительных чисел.
представляет собой множество всевозможных
упорядоченных пар действительных чисел.
Пример
1.
Даны множества
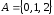 и
и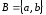 .
Найдите множества
.
Найдите множества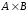 и
и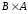 ,
,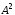 и соответствующие мощности.
и соответствующие мощности.
Решение
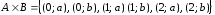 ;
;
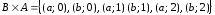 .
.
Найдем
мощность:
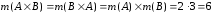 .
.
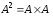 .
.
 .
.
Найдем
мощность:
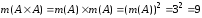 .
.
Пример
2.
Даны множества
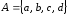 ,
,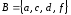 ,
,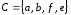 .Найдите
число элементов декартова произведения
множеств
.Найдите
число элементов декартова произведения
множеств
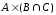 и укажите эти элементы.
и укажите эти элементы.
Решение
Найдем
пересечение множеств
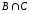 ,
содержащее общие элементы обоих множеств:
,
содержащее общие элементы обоих множеств: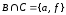 .
Так как множество
.
Так как множество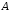 содержит четыре элемента, а множество
содержит четыре элемента, а множество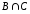 – два элемента, то количество
соответствующих пар декартова произведения
будет
– два элемента, то количество
соответствующих пар декартова произведения
будет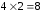 .
Перечислим всевозможные пары:
.
Перечислим всевозможные пары: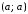 ,
, ,
,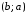 ,
,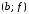 ,
,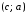 ,
,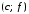 ,
,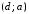 ,
, .
.
Пример
3.
Даны множества
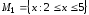 и
и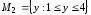 .
Найдите и изобразите на координатной
плоскости
.
Найдите и изобразите на координатной
плоскости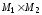 .
.
Решение
В
соответствии с определением декартова
произведения
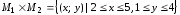 – множество точек, расположенных в
квадрате с вершинами
– множество точек, расположенных в
квадрате с вершинами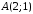 ,
,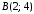 ,
,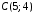 и
и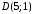 (рис.
10).
(рис.
10).
Понятие
декартова произведения можно обобщить
на случай
 множеств. Если
множеств. Если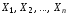 – произвольные непустые множества, то
их декартово произведение
– произвольные непустые множества, то
их декартово произведение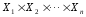 состоит из всевозможных упорядоченных
наборов
состоит из всевозможных упорядоченных
наборов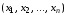 ,
где
,
где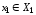 ,
,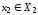 ,
…,
,
…,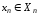 .
.
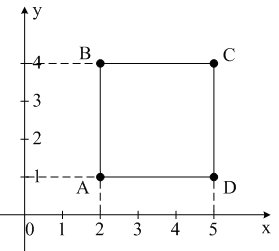
Рис. 10
Замечание.
Если
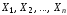 – конечные множества, то
– конечные множества, то
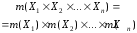 .
.
Декартово произведение множеств само является множеством, и поэтому к нему применимы все изученные ранее способы задания и операции.
Вопросы и задачи для самостоятельного решения
Дайте определение декартова произведения множеств.
Пусть
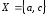 и
и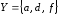 .
Найдите множества
.
Найдите множества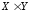 ,
,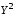 ,
,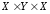 и соответствующие мощности.
и соответствующие мощности.Декартово произведение имеет вид
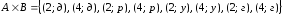 .
Тогда чему равны множества
.
Тогда чему равны множества
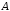 и
и
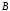 ?
?
1.6. Бинарные отношения. Свойства бинарных отношений
Определение
1.
Бинарным
отношением
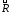 на множествах
на множествах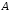 и
и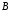 называется любое подмножество декартова
произведения множеств
называется любое подмножество декартова
произведения множеств и
и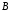 :
: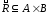 .
При этом множество
.
При этом множество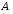 называютобластью
определения
отношения
называютобластью
определения
отношения
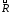 ,
а множество
,
а множество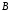 –областью
значений.
–областью
значений.
Если
элементы
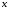 и
и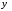 множеств
множеств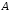 и
и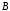 находятся в отношении
находятся в отношении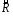 ,
то пишут
,
то пишут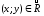 ,
или
,
или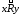 .
Если
.
Если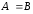 ,
то
,
то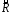 называется
бинарным отношением на
называется
бинарным отношением на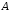 .
.
Например:
а)
если
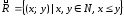 ,
тогда запись
,
тогда запись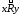 означает, что
означает, что и
в качестве обозначения этого отношения
можно взять сам символ «≤». Множество
определения и множество значений
совпадают с множеством натуральных
чисел;
и
в качестве обозначения этого отношения
можно взять сам символ «≤». Множество
определения и множество значений
совпадают с множеством натуральных
чисел;
б)
если
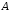 – множество товаров в магазине, а
– множество товаров в магазине, а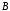 – множество целых положительных чисел
из некоторого диапазона, то
– множество целых положительных чисел
из некоторого диапазона, то
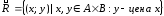 – отношение множеств
– отношение множеств
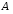 и
и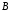 .
Множество определения – товары в
магазине, а множество значений –
действительные числа, каждое из которых
совпадает с ценой некоторого товара;
.
Множество определения – товары в
магазине, а множество значений –
действительные числа, каждое из которых
совпадает с ценой некоторого товара;
c)
если
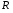 – множество действительных чисел, то
– множество действительных чисел, то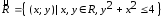 есть бинарное отношение – точки
плоскости, лежащие внутри или на границе
круга радиуса 2 с центром в начале
координат. Множество определения
есть бинарное отношение – точки
плоскости, лежащие внутри или на границе
круга радиуса 2 с центром в начале
координат. Множество определения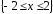 и
множество значений
и
множество значений
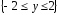 .
.
Свойства бинарных отношений
1.
Бинарное
отношение
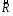 на
множестве
на
множестве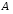 рефлексивное,
если для всякого
рефлексивное,
если для всякого
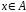 выполняется
выполняется .
.
2.
Бинарное
отношение
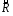 на множестве
на множестве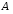 антирефлексивное,
если для любых
антирефлексивное,
если для любых
 и
и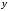 ,
для которых выполнено
,
для которых выполнено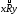 ,
следует, что
,
следует, что .
.
3.
Бинарное отношение
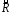 на множестве
на множестве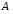 симметричное,
если из выполнения
симметричное,
если из выполнения
 следует, что
следует, что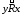 ,
т. е. из принадлежности отношению
пары
,
т. е. из принадлежности отношению
пары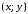 следует принадлежность этому отношению
также пары
следует принадлежность этому отношению
также пары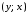 .
.
4.
Бинарное
отношение
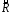 на множестве
на множестве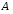 антисимметричное,
если из выполнения
антисимметричное,
если из выполнения
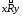 и
и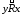 следует,
что
следует,
что
 .
.
5.
Бинарное
отношение
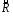 на множестве
на множестве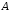 транзитивное,
если из выполнения
транзитивное,
если из выполнения
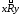 и
и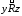 следует выполнение
следует выполнение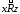 .
.
Определение
2.
Рефлексивное, симметричное и транзитивное
отношение
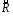 на множестве
на множестве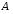 называетсяотношением
эквивалентности.
называетсяотношением
эквивалентности.
Определение
3.
Рефлексивное, антисимметричное и
транзитивное отношение
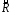 на множестве
на множестве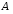 называетсяотношением
нестрогого порядка.
называетсяотношением
нестрогого порядка.
Определение
4.
Антирефлексивное, антисимметричное и
транзитивное отношение
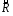 на множестве
на множестве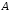 называетсяотношением
строгого порядка.
называетсяотношением
строгого порядка.
Пример. Проверьте, какими свойствами обладает отношение
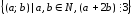 (т.е.
(т.е.
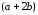 кратно трем).
кратно трем).
Решение:
а)
рефлексивность: для
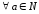 и
и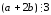 необходимо показать, что
необходимо показать, что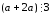 .
.
Действительно,
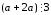
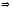
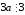
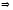 отношение рефлексивно;
отношение рефлексивно;
б)
симметричность: для
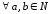 и
и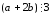 необходимо показать, что
необходимо показать, что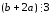 .
.
Обозначим

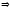
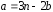 ,
подставим:
,
подставим:
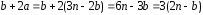

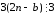
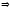 отношение
симметрично;
отношение
симметрично;
в)
транзитивность: для
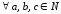 и
и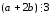 ,
,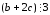 необходимо показать, что
необходимо показать, что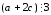 .
.
Обозначим
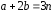
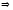
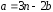 ,
и
,
и
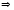
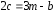 ,
подставим:
,
подставим:
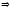
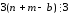
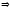 отношение
транзитивно.
отношение
транзитивно.
Так как отношение рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Вопросы и задачи для самостоятельного решения
1. Какие отношения называют отношением эквивалентности, отношением нестрогого порядка, отношением строгого порядка?
2. Найдите область определения и множество значений отношений:
а)
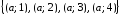 ;
;
б)
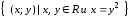 .
.
3.
Даны множества
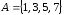 и
и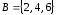 .
Найдите количество пар, удовлетворяющих
бинарному отношению
.
Найдите количество пар, удовлетворяющих
бинарному отношению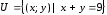 .
.
