
- •В.С. Васильева, с.В. Коровина, л.В. Марченко дискретная математика
- •Васильева, в.С.
- •Введение
- •1. Элементы теории множеств
- •1.1. Основные понятия теории множеств. Способы задания множеств
- •1.2. Операции над множествами
- •1.3. Диаграммы Эйлера – Венна
- •1.4. Свойства операций над множествами
- •1.5. Декартово произведение множеств
- •1.6. Бинарные отношения. Свойства бинарных отношений
- •1.7. Функция
- •2. Элементы математической логики
- •2.1. Математическая логика как наука
- •2.2. Высказывания. Логические операции и их основные свойства
- •Логические операции
- •Новые логические операции
- •2.3. Способы решения логических задач
- •2.4. Булевы функции. Свойства элементарных булевых функций
- •2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций
- •2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •3. Элементы теории графов
- •3.1. Основные понятия теории графов
- •3.2. Способы задания графов
- •3.3. Связность графов
- •4. Элементы комбинаторики
- •4.1. Перестановки, размещения и их количество
- •4.2. Сочетания и их свойства
- •4.3. Выборки с повторением
- •5. Индивидуальные задания
- •Заключение
- •Библиографический список
- •Оглавление
1.2. Операции над множествами
Пусть
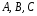 – произвольные множества. Определим
операции над ними.
– произвольные множества. Определим
операции над ними.
Определение
1.
Объединением
двух множеств называется множество,
состоящее из всех элементов, принадлежащих
хотя бы одному из этих множеств.
Обозначение:
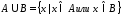 .
.
Определение
2.
Пересечением
двух множеств называется множество,
состоящее из всех элементов, принадлежащих
одновременно обоим множествам.
Обозначение:
 .
.
Определение
3.
Разностью
множества
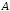 и
и (дополнением
множества
(дополнением
множества
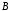 до множества
до множества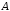 или, иначе говоря,
или, иначе говоря,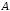 без
без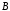 )
называется множество всех элементов
)
называется множество всех элементов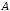 ,
не принадлежащих
,
не принадлежащих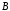 .
Обозначение:
.
Обозначение: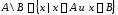 .
.
Определение
4.
Дополнением
(до
универсального множества
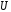 )
множества
)
множества
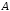 называется множество всех элементов,
не принадлежащих
называется множество всех элементов,
не принадлежащих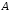 .
Обозначение:
.
Обозначение: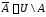 .
В некоторых случаях запись
.
В некоторых случаях запись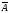 означает
разность не с универсальным множеством,
а с множеством, определенным в условии
задачи как множество, содержащее
означает
разность не с универсальным множеством,
а с множеством, определенным в условии
задачи как множество, содержащее
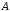 .
.
Определение
5.
Симметрической
разностью
(или
кольцевой суммой)
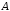 и
и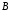 называется множество
называется множество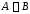 (или
(или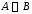 ),
куда входят все те элементы множества
),
куда входят все те элементы множества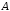 ,
которые не входят в множество
,
которые не входят в множество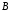 ,
а также элементы
,
а также элементы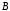 ,
которые не входят в
,
которые не входят в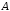 ,
т. е.
,
т. е.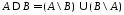 .
.
Замечание.
Симметрическую разность можно записать
в виде
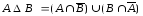 .
.
Перечисленные операции позволяют выражать одни множества через другие. При этом используется следующий порядок выполнения операций: операция дополнения, пересечения, объединения и разности. Если есть скобки, то сначала выполняются операции в скобках.
Пример
1. Пусть
заданы множества:
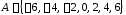 ,
,
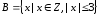 и
и
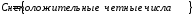 .
Найдите:
.
Найдите:
а)
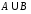 ;
в)
;
в)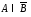 ;
д)
;
д)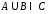 ;
;
б)
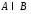 ;
г)
;
г)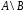 ;
е)
;
е)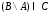 .
.
Решение
а)
множество
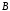 состоит
из элементов:
состоит
из элементов:
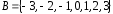 .
Так
как объединению множеств
.
Так
как объединению множеств
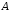 и
и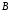 принадлежат элементы, входящие или во
множество
принадлежат элементы, входящие или во
множество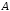 или во множество
или во множество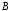 ,
причем одинаковые элементы включаются
только один раз, то
,
причем одинаковые элементы включаются
только один раз, то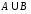
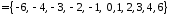 ;
;
б)
так как пересечению множеств
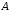 и
и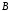 принадлежат элементы, входящие
одновременно в оба множества
принадлежат элементы, входящие
одновременно в оба множества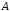 и
и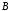 ,
то
,
то ;
;
в)
множество
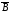 следует понимать как
следует понимать как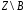 ,
т. е. как множество целых чисел
,
т. е. как множество целых чисел ,
удовлетворяющих соотношению
,
удовлетворяющих соотношению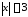 :
: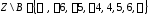 .
Общими элементами указанного множества
и множества
.
Общими элементами указанного множества
и множества
 являются четыре целых числа
являются четыре целых числа
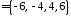 ;
;
г)
разность множеств содержит те элементы
множества
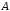 ,
которые не принадлежат множеству
,
которые не принадлежат множеству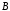 ,
поэтому
,
поэтому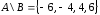 ;
;
д)
при нахождении значения выражений,
содержащих несколько операций, следует
соблюдать порядок выполнения операций,
если он не указан с помощью скобок.
Операция пересечения имеет больший
приоритет, чем объединение.
Поэтому первоначально найдем пересечение
множеств
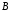 и
и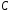 :
:
 .
.
Окончательно
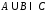
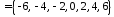 ;
;
е)
найдем сначала разность множеств
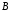 и
и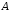 :
: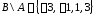 .
Окончательно
.
Окончательно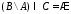 .
.
Пример
2.
Даны два множества
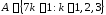 и
и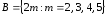 .
Найдите количество элементов, принадлежащих
симметрической разности
.
Найдите количество элементов, принадлежащих
симметрической разности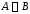 .
.
Решение
Выпишем
элементы, из которых состоят множества
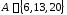 и
и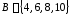 .
Тогда
.
Тогда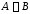
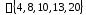 ,
т. е. симметрическая разность состоит
из пяти элементов.
,
т. е. симметрическая разность состоит
из пяти элементов.
Вопросы и задачи для самостоятельного решения
Дайте определения объединения, пересечения, разности и дополнения множеств.
2. Укажите порядок выполнения операций над множествами.
3. Запишите, используя символику теории множеств:
а)
множество
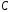 – дополнение к пересечению множеств
– дополнение к пересечению множеств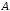 и
и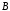 ;
;
б)
множество, состоящее из всех элементов
множеств
 и
и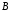 ;
;
в)
множество, состоящее из элементов
множества
 ,
но не включающее элементы множеств
,
но не включающее элементы множеств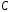 .
.
4. Дано
множество
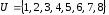 и его подмножества
и его подмножества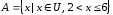 ,
,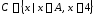 и
и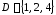 .
Найдите множества:
.
Найдите множества:
а)
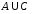 ;
в)
;
в)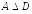 ;
;
б)
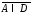 ;
г)
;
г)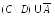 .
.
5.
Даны множества
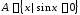 и
и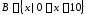 .
Найдите мощность множества
.
Найдите мощность множества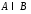 .
.
6.
Пусть
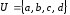 ,
,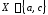 ,
,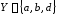 и
и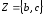 .
Найдите мощности следующих множеств:
.
Найдите мощности следующих множеств:
а)
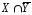 ;
г)
;
г)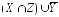 ;
;
б)
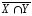 ;
д)
;
д)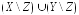 ;
;
в)
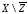 ;
е)
;
е)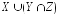 .
.
7. Даны
два множества:
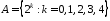 и
и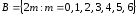 .
Найдите количество элементов, принадлежащих
множеству
.
Найдите количество элементов, принадлежащих
множеству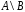 .
.
8.
Даны множества:
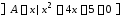 ,
,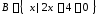 и
и
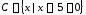 .
Найдите мощность множества
.
Найдите мощность множества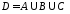 .
.
9.
Пусть
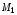 ,
,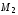 ,
, – множества, состоящие из всех чисел,
кратных 2, 3, 5 соответственно. С помощью
операций над множествами выразите через
них множества чисел: а) делящихся на 6;
б) делящихся на 30; в) делящихся на 10, но
не делящихся на 3.
– множества, состоящие из всех чисел,
кратных 2, 3, 5 соответственно. С помощью
операций над множествами выразите через
них множества чисел: а) делящихся на 6;
б) делящихся на 30; в) делящихся на 10, но
не делящихся на 3.
