Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

ГОУ ВПО «Дальневосточный государственный

университет путей сообщения»

Институт тяги подвижного состава

Кафедра «детали машин»

Курсовая работа

По дисциплине «Теория механизмов и машин»

На тему: «Исследование рычажного механизма»

Студент: Ким Ун Нам

Специальность: «Подвижной состав железных дорог»

Преподаватель: Поспелов Александр Иванович

Южно-Сахалинск

2014

Введение

Теория механизмов и машин (ТММ) является основой проектирования работоспособных технических объектов. Основные задачи ТММ – это анализ и синтез механизмов с заданными параметрами, и проектирование механизмов (определение его параметров), удовлетворяющих заданным требованиям. Результаты решения задач ТММ являются исходными данными для более детального проектирования объектов методами деталей машин, сопротивления материалов и специальных дисциплин.

Цель работы

Целью выполнения данной курсовой работы является закрепление теоретических сведений, полученных при изучении «Теории механизмов и машин», приобретение практических навыков конструирования рычажных механизмов.

В данной работе рассматривается механизм состоящий из трех звеньев и трех кинематических пар.

Исследование рычажного механизма включает три этапа:

1. Структурный анализ механизма.

2. Кинематический анализ.

3. Кинетостатический анализ.

Исходные данные
параметры	значения
ℓAB, мм	60
ℓBC, мм	150
ω1, рад/с	10
φ, градусы	150
ε1, рад/с	0
m1, кг	4
m2, кг	3
m3, кг	0,15
F, H	30

1 Структурный анализ механизма

Структурная схема механизма изображена на рисунке 1

Рисунок 1 – структурная схема механизма

Степень подвижности механизма определяется по формуле

Чебышева [1]

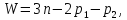
Где n – число подвижных звеньев механизма;

p₁ – число одноподвижных кинематических пар;

p₂– число двухподвижных кинематических пар.

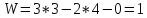
Данный механизм имеет первую степень подвижности.

Первичный механизм изображен на рисунке 2

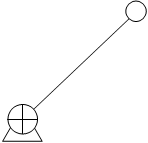
Рисунок 2 - первичный механизм I кл

Группа Ассура изображена на рисунке 3

Рисунок 3 - группа АссураIIкл, 1 вида

Механизм изображенный на рисунке 1 II класса.

2 Кинематическое исследование механизма

Существует три метода кинетического анализа механизма:

1. Аналитический

2. Метод диаграмм

3. Метод планов.

2.1 План скоростей и его свойства

Планом скоростей механизма называют совокупность планов скоростей отдельных звеньев механизма имеющих общий полюс.

Скорость точки Bопределяется из уравнения

,

Где – вектор скорости точки A;

– вектор скорости точки В относительно точки А.

Скорость точки А равна нулю.

Скорость точки В относительно точки А определяется из уравнения

*

Скорость точки В относительно точки А равна 0,6 м/с.

Масштабный коэффициент плана скоростей определяется из уравнения

,

Где 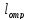– длинна отрезка на чертеже.

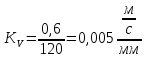
Масштабный коэффициент плана скоростей равен 0,005(м⁄с)/мм.

Скорость точки С определяется из уравнения

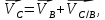
Где – скорость точки С относительно точки В.

Скорость точки С относительно точки В определяется из уравнения

Так как нам неизвестна угловая скорость , составляется система уравнений.

,

Где – скорость точки находящейся на стойке;

– скорость точки С относительно точки С4.

Свойства плана скоростей:

1. Вектора абсолютных скоростей точек звеньев механизма выходит из точки, а относительные соединяют концы абсолютных.

2. По плану скорости можно определить направление и величину абсолютной скорости звена механизма.

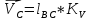
Скорость точки С равна 0,63 м/с

3. По плану скорости можно определить направление и величину угловой скорости любого звена механизма.

Угловая скорость второго звена определяется из уравнения

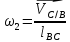
Отрезок BCна плане скоростей является скоростью

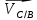
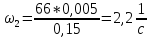
Угловая скорость 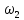второго звена равна 2,2 1/с

4. Свойство подобия. Фигура на плане механизма подобна фигуре на плане скоростей.

Длина отрезка 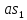определяется из уравнения

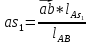
Скорость точки s₁определяется из уравнения

Скорость точки s₁равна 0,3 м/с

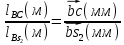
Длина отрезка 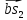определяется из уравнени

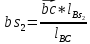
Скорость точки 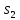определяется из уравнения

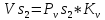
Скорость точки 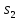равна 0,595 м/с

Скорость точки определяется из уравнения

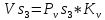
Скорость точки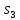 равна 0,63 м/с.

2.2 План ускорений и его свойства

Планом ускорений механизма называется совокупность планов ускорений отдельных его звеньев, имеющих общий полюс.

Нормальное ускорение определяется по формуле

Тангенсальное ускорение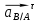 определяется из уравнения

Ускорение точки В определяется из уравнения

Где – нормальное (центростремительное) ускорение точки В относительно точки А;

– тангенсальное ускорение точки В относительно точки А равное 0;

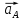– ускорение точки А равное 0, так как она неподвижна.

Ускорение равно 6 м/с²

Масштабный коэффициент определяется из уравнения

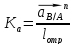
Масштабный коэффициент равен 0,05 (м/с²)/мм

Нормальное ускорение 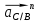определяется из уравнения

Величину отрезка определим из уравнения

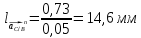
Ускорение точки С определяется из системы уравнений

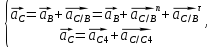
Где 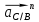–нормальное (центростремительное) ускорение точки С относительно точки В;

- тангенсальное ускорение точки С относительно точки В.

– ускорение точки С4 равное 0;

– ускорение точки С относительно С4.

Ускорение определяется из уравнения

Ускорение точки С равно 2,1 м/с²

Свойства плана ускорений:

1. Вектора абсолютных ускорений точек звеньев механизма выходят из полюса, а относительные соединяют концы абсолютных.

2. По плану ускорений можно определить направление и величину ускорения в любой точке звена механизма.

3. По плану ускорений можно определить направление и величину углового ускорения любого звена механизма.

4. Свойство подобия. Фигура на плане механизма подобна фигуре на плане ускорений.

Ускорение центра масс первого, второго и третьего звеньев определяется из уравнения

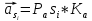
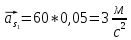
3. Кинето-статический расчет механизма.

Вес узлов определяется из уравнения

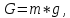
где m - масса узла;

g - ускорение свободного падения.

Вес G узлов 1, 2 и 3 определяются из уравнений

Сила инерции 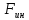определяется из уравнения

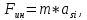
где m - масса звена;

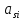- ускорение центра масс.

Сила инерции узлов 1, 2 и 3 определяются из уравнений

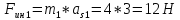
Момент сил инерции M_ин определяется из уравнения

где - момент инерции;

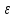- угловое ускорение.

Моменты сил инерции звеньев 1 и 2 определяются из уравнений

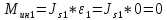
так как =0

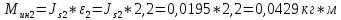
Момент инерции определяется из уравнения

Момент инерции звена 2 определяется из уравнения

Величина h₁ определяется из уравнения

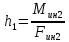
Уравнение равновесия

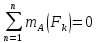
Из уравнения равновесия определяем

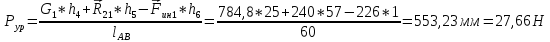
4. Рычаг Жуковского

Уравнение равновесия

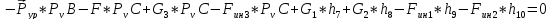
Из уравнения равновесия определяем

5. Список литературы

1. Теория механизмов и машин: Учеб. Для вузов. – 6-е изд., стереотипное. – М.: ИД Альянс, 2011. – 640с.

2. Курсовое проектирование по теории механизмов и машин: Учеб. Пособие для машиностроит. спец. вузов/ Под ред. К.В. Фролова. – М.: высш. шк., 1986. – 295 с.: ил.

Содержание