
- •2.6. Представление синусоидальных функций времени комплексными числами
- •2.7. Способы задания синусоидального тока
- •2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
- •2.9. Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении
- •2.10. Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности
- •2.11. Синусоидальный ток в емкости
- •2.12. Последовательное соединение активного сопротивления, индуктивности и емкости
- •2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
- •2.14. Пассивный двухполюсник в цепи синусоидального тока.Эквивалентные сопротивления и проводимости
- •2.15. Закон Ома в символической форме для произвольной цепи

где
![]() ;
;
![]() .
.
2.6. Представление синусоидальных функций времени комплексными числами
Рис.
2.13. Вектор тока на
комплексной
плоскости

![]() ,
которое называется комплексной
амплитудой тока.
,
которое называется комплексной
амплитудой тока.
Комплексное
действующее значение тока получается
делением последнего выражения
на
![]() :
:
![]() .
.
Здесь
и дальше буквами с точкой над ними (![]() )
обозначаются комплексные числа,
представляющие синусоидальные функции
времени. Это ток, напряжение и ЭДС.
Комплексные сопротивление и проводимость
обозначаются прописными буквами Z
и
Y
,
а их модули строчными z
и
y.
Комплексная
мощность обозначается буквой S
с волнистым значком
(тильда)
над ней:
)
обозначаются комплексные числа,
представляющие синусоидальные функции
времени. Это ток, напряжение и ЭДС.
Комплексные сопротивление и проводимость
обозначаются прописными буквами Z
и
Y
,
а их модули строчными z
и
y.
Комплексная
мощность обозначается буквой S
с волнистым значком
(тильда)
над ней:
![]() .
.
2.7. Способы задания синусоидального тока
Как следует из вышесказанного, синусоидальный ток можно задать четырьмя различными формами: уравнением i = Imsin(t + ), определяющим мгновенное значение тока (значение тока в любой момент времени), волновой диаграммой, вектором и комплексным числом. При этом мы легко можем перейти от одной формы задания к другой.

Например:
1) i = 20sin(t+110),
![]() ,
,
![]() ;
;

2)
![]() ,
,
![]() ,
,
i = 8,49sin(t-60);

3)
![]() ,
,
i = 5sin(t-143,1),
![]() ,
,

u = 100 sin (t + 60).
В качестве начальной фазы мы берем не 120, которые указаны на волновой диаграмме, а тот угол, на который сдвинуто начало синусоиды. Начальная фаза на волновой диаграмме определяется ближайшей к началу координат точкой перехода синусоиды через ноль от минуса к плюсу – это 60. Так как начало синусоиды смещено от точки 0 влево, то начальная фаза положительна.
2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
П е р в ы й: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
![]() ,
(2.8)
,
(2.8)
где n – число ветвей, сходящихся в узле.
В т о р о й: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
![]() , (2.9)
, (2.9)
где m – число ветвей, образующих контур.
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
|
Законы Кирхгофа в векторной форме: |
Законы Кирхгофа в символической форме: |
|
|
|
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (2.8) и (2.9); применение метода векторных диаграмм, основанного на уравнениях (2.10), использование в расчетах комплексных чисел и уравнений (2.11), являющихся основой символического метода.
Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 2.14).
Рис.
2.14. Узел электрической цепи

i1 = 8sin(t+30) А,
i2 = 6sin(t+120) А.
Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы.
Р е ш е н и е. 1. Непосредственное сложение синусоид:
i3 = i1+i2 = 8sin(t+30)+6sin(t+120) = I3msin(t+3).
Сумма двух синусоид одинаковой частоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:
![]()
![]() A,
A,
![]() ,
,
откуда 3 = 66,87. Итак, i3 = 10sin (t+66,87).
2. Применение метода векторных диаграмм.
Рис.
2.15. Векторная диаграмма токов

![]() .
В прямоугольной системе координат
строим векторы
.
В прямоугольной системе координат
строим векторы
![]() и
и
![]() и находим вектор
и находим вектор
![]() ,
равный их сумме (рис. 2.15).
,
равный их сумме (рис. 2.15).
Так
как треугольник oab
прямоугольный,
а сторона ab
равна длине вектора I2m,
то
![]() =
=
![]() А.
А.
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси:
![]()
![]()
3. Решение символическим методом.
Записываем комплексные амплитуды первого и второго токов:
![]() A,
A,
![]() A.
A.
По первому закону Кирхгофа в символической форме
![]() А.
А.
Модуль последнего комплексного числа равен амплитуде третьего тока, а аргумент – начальной фазе.
Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, поэтому
![]() A,
A, ![]() A,
A, ![]() A.
A.
Обращаем
внимание на то, что
![]() .
Это не ошибка. В
цепях синусоидального тока для показаний
приборов законы Кирхгофа не справедливы.
Можно складывать мгновенные значения
токов (синусоидальные функции времени),
векторы и комплексные числа, но не
численные значения токов и напряжений,
не показания приборов.
.
Это не ошибка. В
цепях синусоидального тока для показаний
приборов законы Кирхгофа не справедливы.
Можно складывать мгновенные значения
токов (синусоидальные функции времени),
векторы и комплексные числа, но не
численные значения токов и напряжений,
не показания приборов.
Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.
Метод векторных диаграмм удобен при решении относительно несложных задач.
В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.

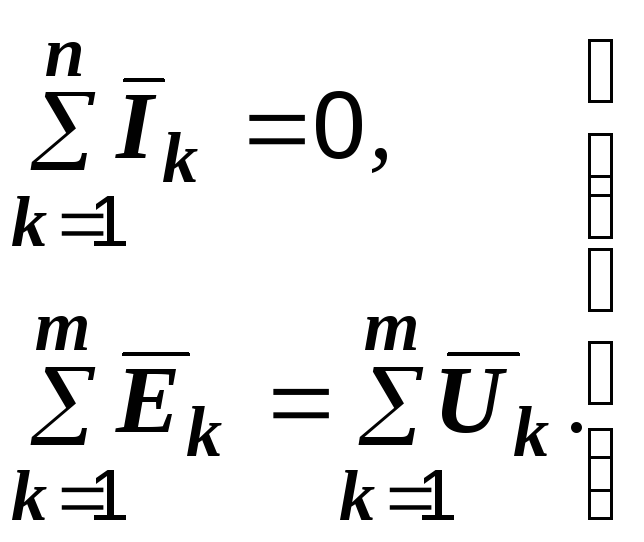 (2.10)
(2.10) (2.11)
(2.11)