
- •Электричество и магнетизм Сборник задач по курсу общей физики
- •Предисловие
- •Глава 1. Закон Кулона. Закон сохранения электрического заряда. Напряженность электрического поля Основные формулы
- •Примеры решения задач
- •Глава 2. Электрический диполь Основные формулы
- •Примеры решения задач
- •Глава 3. Вычисление полей с помощью теоремы Гаусса Основные формулы
- •Примеры решения задач
- •Глава 4. Электрическая емкость. Конденсаторы Основные формулы
- •Примеры решения задач
- •Глава 5. Энергия системы точечных зарядов Основные формулы
- •Примеры решения задач
- •Глава 6. Закон полного тока. Магнитный поток. Магнитные цепи. Сверхсильные магнитные поля Основные формулы и соотношения
- •Примеры решения задач
- •Глава 7. Действие магнитного поля на ток и заряд Основные формулы и соотношения
- •Примеры решения задач
- •Глава 8. Магнитный поток. Работа по перемещению проводника с током в магнитном поле Основные формулы и соотношения
- •Глава 9. Закон электромагнитной индукции. Индуктивность. Энергия магнитного поля
- •Основные формулы и соотношения
- •Примеры решения задач
- •Глава 10. Магнитное поле в веществе. Магнитные жидкости Основные формулы и соотношения
- •Примеры решения задач
- •Глава 11. Уравнения максвелла Основные формулы и соотношения
- •Примеры решения задач
- •Заключение
Глава 6. Закон полного тока. Магнитный поток. Магнитные цепи. Сверхсильные магнитные поля Основные формулы и соотношения
Циркуляция вектора магнитной индукции В вдоль замкнутого контура:
![]() Вdl
=
Вdl
=
![]() Вl dl
,
(6.1)
Вl dl
,
(6.1)
где
![]() – проекция вектора магнитной индукции
на направление элементарного перемещенияdl
вдоль контура L.
– проекция вектора магнитной индукции
на направление элементарного перемещенияdl
вдоль контура L.
Циркуляция вектора напряженности H вдоль замкнутого контура
![]() Hdl
=
Hdl
=
![]() Нl dl.
(6.2)
Нl dl.
(6.2)
2. Закон полного тока для магнитного поля в вакууме:
![]() Вdl
Вdl![]() ,
(6.3)
,
(6.3)
где
μ0
– магнитная постоянная; n
– число токов;
![]() –
алгебраическая
сумма токов, охватываемых контуром.
–
алгебраическая
сумма токов, охватываемых контуром.
Закон полного тока (для произвольной среды) имеет вид:
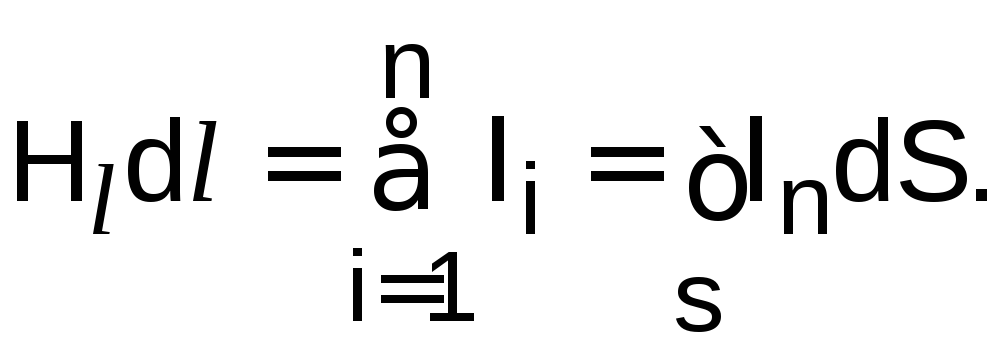
![]()
3. Магнитное поле тороида, сердечник которого составлен из двух частей, изготовленных из веществ с различными проницаемостями:
магнитная индукция на осевой линии тороида имеет вид:
 (6.5)
(6.5)
где
I
– сила тока в обмотке тороида; N
– число витков в обмотке;
![]() – длины первой второй частей сердечника
тороида; μ1
и μ2
– магнитная проницаемость первой и
второй частей сердечника тороида; μ0
– магнитная постоянная;
– длины первой второй частей сердечника
тороида; μ1
и μ2
– магнитная проницаемость первой и
второй частей сердечника тороида; μ0
– магнитная постоянная;
напряженность магнитного поля на осевой линии тороида в первой и второй частях сердечника (с магнитными проницаемостями μ1 и μ2):
![]() .
(6.6)
.
(6.6)
4. Магнитный поток в сердечнике тороида
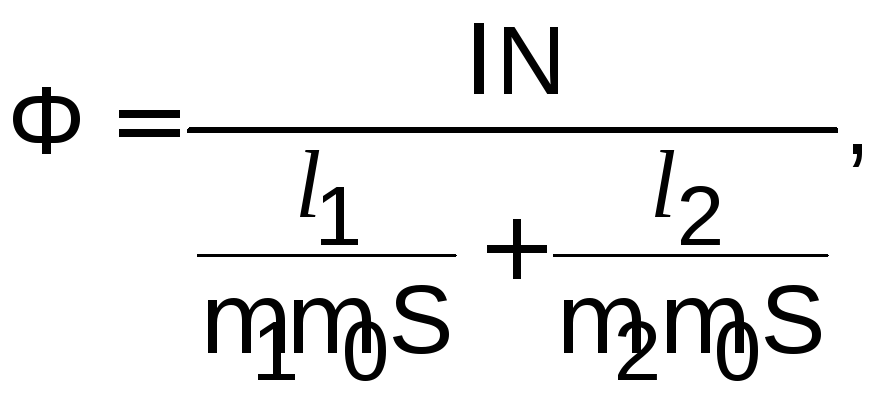 (6.7)
(6.7)
или по аналогии с законом Ома
 (6.8)
(6.8)
это формула Гопкинса, где Fm – магнитодвижущая сила; Rm – полное магнитное сопротивление.
5. Магнитное сопротивление участка цепи определяется выражением
 (6.9)
(6.9)
где l – длина участка; μ – магнитная проницаемость участка; S – сечение тороида.
6. Связь между вектором магнитной индукции В поля в железе и напряженностью поля Н намагничивающего поля выражается графиком (рис. 6.1).

Рис. 6.1. График зависимости В = В(Н) для железа, чугуна и стали
Примеры решения задач
Пример 1. Определить индукцию В и напряженность Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N = 200 витков, идет ток = 10 А. Внешний диаметр d1 тороида равен 30 см, внутренний d2 = 20 см.
Решение.
Для определения напряженности магнитного
поля внутри тороида вычислим циркуляцию
вектора Н вдоль силовой линии напряженности
поля
![]() Нl dl.
Нl dl.
Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и во всех точках этой линии напряженность Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2r, где r – радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т. е.
![]() Н dl
=
Н dl
=
 (6.10)
(6.10)
С другой стороны, в соответствии с законом полного тока циркуляция вектора напряженности магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:
![]() Нl dl
Нl dl
![]() (6.11)
(6.11)
Приравнивая правые части соотношений (6.10) и (6.11), получим
![]() (6.12)
(6.12)
Линия, проходящая вдоль тороида, охватывает число токов, равное числу векторов тороида. Сила тока во всех витках одинакова. Поэтому формула (6.12) примет вид: 2rН = NI, откуда
![]() (6.
13)
(6.
13)
Для средней линии тороида r = 0,5(R1 + R2) = 0,25(d1 + d2).
Подставив это выражение r в формулу (6.13), получим
![]() (6.14)
(6.14)
Магнитная индукция Во в вакууме связана с напряженностью поля соотношением Во = μ0Н. Следовательно,
![]() (6.15)
(6.15)
Подставив значение величин в выражения (6.14) и (6.15), получим
Н = 2,74 кА/м; В0 = 3,2 мТл.
Пример 2. Чугунное кольцо имеет воздушный зазор длиной l0 = 5 мм. Длина l средней линии кольца равна 1 м. Сколько витков N содержит обмотка на кольце, если индукция В магнитного поля в воздушном зазоре равна 0,5 Тл. Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать.
Решение. Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна индукции поля в чугуне. На основании закона полного тока запишем
IN = Hl + H0 l0.
По графику (см. рис. 6.1) находим, что при В = 0,5 Тл напряженность Н магнитного поля в чугуне равна 1,2 кА/м. Так как для воздуха μ = 1, то напряженность поля в воздушном зазоре следующая:
H0 = B/ μ0 = 0,4 мА/м.
Искомое число витков будет N = (Hl + H0 l0) = 800.
Задачи
601.
Определить циркуляцию магнитной индукции
по контуру квадрата, если через его
центр, перпендикулярно плоскости, в
которой он лежит, проходит бесконечно
длинный прямолинейный провод, по которому
течет ток I= 1А. (Ответ:![]() ).
).
602.
Найти циркуляцию вектора Н в двух случаях
(рис. 6.2, а, б), если сила тока в обоих
проводниках= 8 А и
токи имеют противоположные направления.
(Ответ: а) Нldl= 0; б) Нldl= 16 А![]() м).
м).
а б


Рис. 6.2
603.
Тонкое железное кольцо со средним
диаметром d= 50 см несет
на себе обмотку изN= 850
витков с током=
3,0 А. В кольце имеется поперечная прорезь
ширинойd= 2 мм. Пренебрегая
рассеянием магнитного потока на краях
зазора, найти с помощью графикаB= В(Н) магнитную проницаемость железа.
Указание: Воспользоваться законом
полого тока для Н. (Ответ: Н = 0,26 кА/м;
В = 1,25 Тл; μ = 4![]() 103).
103).
604.
На железном сердечнике в виде тора со
средним радиусом
R= 250
мм имеется обмотка с общим числом витковN= 1000. В сердечнике сделана
прорезь ширинойb= 1,00 мм.
При токеI= 0,85 А через обмотку индукция магнитного
поля в зазоре В = 0,75 Тл. Пренебрегая
рассеянием магнитного потока на краях
зазора, найти магнитную проницаемость
железа в этих условиях. (Ответ: μ =
3.7![]() 103).
103).
605.
Ток идет по полой металлической трубе.
Вычислить: 1) напряженность поля внутри
трубы; 2) напряженность поля вне трубы
на расстоянии rот
поверхности, если внешний радиус трубыRи величина токаI.
(Ответ: Н1= 0;![]() ).
).
606. Электромагнит изготовлен в виде тороида. Сердечник тороида со средним диаметром d= 51 см имеет вакуумный зазор длинойl0= 2 мм. Обмотка тороида равномерно распределена по всей его длине. Во сколько раз уменьшиться индукция магнитного поля в зазоре, если, не изменяя силы тока в обмотке, зазор увеличить вn= 3 раза? Рассеянием магнитного поля вблизи зазора пренебречь. Магнитную проницаемость μ сердечника считать постоянной и принять равной 800. (Ответ: в 2 раза).
607. Диаметр Dтороида без сердечника по средней линии равен 30 см. В сечении тороид имеет круг радиусомr= 5 см. По обмотке тороида, содержащейN= 2000 витков, течет токI= 5 А. Пользуясь законом полного тока, определить максимальное и минимальное значения магнитной индукции В в тороиде. (Ответ: Вmax = 20 мТл; В min= 10 мТл).
608.
Вычислить циркуляцию вектора индукции
вдоль контура, охватывающего токи I1= 10 А,I2= 15 А, текущие в одном направлении, и токI3
= 20 А, текущий в противоположном
направлении. (Ответ: 6,28
![]() 10-6
Тл
10-6
Тл
![]() м).
м).
609. Определить магнитодвижущую силу Fm, необходимую для создания магнитного поля индукцией В = 1,4 Тл в электромагните с железным сердечником длиной ℓ = 90 см и промежутком длинойl0= 5 мм. Рассеянием магнитного потока пренебречь. Использовать график зависимости В = В(Н). (Ответ:Fm= 7,1 кА).
610. В железном сердечнике соленоида индукция В = 13 Тл. Железный сердечник заменим стальным. Определить во сколько раз следует изменить силу тока в обмотке соленоида, чтобы индукция в сердечнике осталась неизменной. (Ответ: в 2,4 раза).
611.
По сечению проводника равномерно
распределен ток плотностью
j= 2 МА/м2. Найти циркуляцию вектора
напряженности вдоль окружности радиусомR= 5 мм, проходящей внутри
проводника и ориентированной, так, что
ее плоскость составляет угол= 30ос вектором плотности тока.
(Ответ:Hl![]() dl= 78,6 А).
dl= 78,6 А).
612. Вектор магнитной индукции на оси тороида 1,25 Тл. Тороид состоит из двух частей железной и никелевой. Средний радиус тороида 20 см, длина никелевой части сердечника 50 мм. Число витков N = 1000, сила тока I = 1А, магнитная проницаемость железной части сердечника 800. Определить напряженность магнитного поля в железной части сердечника и магнитную проницаемость никеля в этих условиях. (Ответ: H = 1500 А/м; μ Ni = 99).
613.
В условиях предыдущей задачи вычислить
магнитное сопротивление Rmникелевого участка, если площадь сечения
тороидаS= 10 см2.
(Ответ:Rm= 4![]() 105Ом-1
105Ом-1![]() с-1).
с-1).
614.
В работах П.Л. Капицы получены магнитные
поля H= 3![]() 107А/м. Вычислить торцевые сжимающие
напряжения, действующие на соленоид.Изобразить
схематически направления действия этих
сил. (Ответ: Pe
= 109
Па).
107А/м. Вычислить торцевые сжимающие
напряжения, действующие на соленоид.Изобразить
схематически направления действия этих
сил. (Ответ: Pe
= 109
Па).
615.
В условиях предыдущей задачи, но при
токе в соленоиде I= 106А иn= 10 витков/см,
вычислить силу, действующую по торцам
соленоида, если сечение соленоидаS= 10 см2. Показать эти силы схематически.
(Ответ:fe= 62.8![]() 106Н).
106Н).
616.
Короткий соленоид с обмоткой из медной
проволоки имеет n= 10
витков/см, по которым проходит импульсный
токI= 106А. Вычислить механическое
радиальное напряжениеprдля этого соленоида и сравнить его с
пределом прочности меди равным 210 Н/мм2.
Будет ли разрушен соленоид в таком поле?
(Ответ:pr= 6.28![]() 1011Па).
1011Па).
617. Длина железного сердечника тороида l1 = 2,5 м, длина воздушногозазора l2 = 1см. Число витков в обмотке тороида N = 1000. При токе I = 20 Аиндукция магнитного поля в воздушном зазореB= 1,6 Тл. Найти магнитную проницаемость μ железа в этих условиях (зависимость В = В(Н) для данного сорта железа неизвестна). (Ответ: μ = 440).
618.
Пусть тороид имеет квадратное сечение
величиной а, радиус средней линии тороида
равен b, при чемb>>a.
Вычислить относительную ошибку, которую
мы допускаем, считая поле тороида
однородным. (Ответ:![]() ).
).
619.
По толстому прямолинейному проводнику
пропускают ток .
Пусть радиус проводникаR0.
Найти функциональную зависимость Н =H(r), гдеr– координата от центра проводника доR0. Изобразить эту
зависимость графически. (Ответ:![]() ).
).
620.
В экспериментах А.Д. Сахарова в импульсном
режиме были получены магнитные поля до
~ 1010А/м. Принимая, что в этом случае
был короткий соленоид сn= 2 витка/см, вычислить величину
импульсивного тока, а также максимальное
радиальное механическое напряжение
материала соленоида. (Ответ:= 50 А;pr= 6.28![]() 1013Па).
1013Па).
621.
В условиях предыдущей задачи вычислить
сжимающее механическое напряжение,
действующее по торцу соленоида Рl.
Каков будет характер силы взаимодействия
между витками, если импульс тока будет
представлять один период синусоиды сIm= 50 МА. (Ответ: Рl
= 6.28![]() 1013Па).
1013Па).
6
Рис.
6.3
1. Найти магнитную индукцию В в точках rвнутри центрального проводника (r<a).
2. Найти В в пространстве между проводниками (a<r<b).
3. Найти В внутри внешнего проводника (b < r < c).
4. Найти В вне кабеля (r>c).
(Ответ:
1.
![]() ,
0 < r < a; 2.
,
0 < r < a; 2.![]() ,
a < r < b;
3.
,
a < r < b;
3.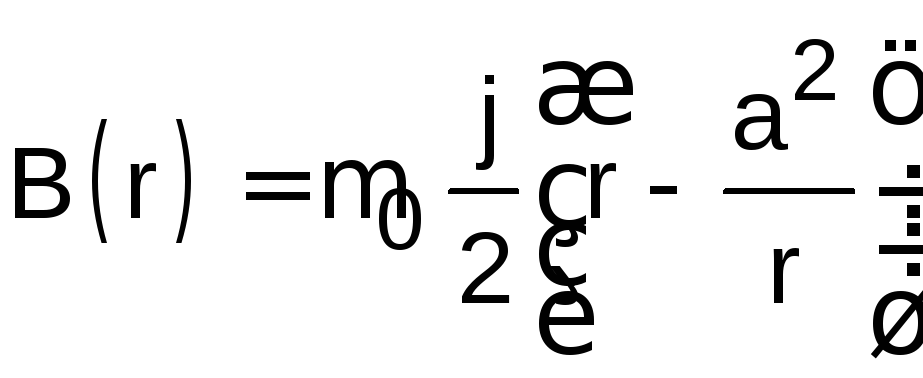 ,
b < r < c; 4.
,
b < r < c; 4.  ,
r > c).
,
r > c).
623.
Тороидальная катушка из Nвитков, внутренний радиус которой равенb, в поперечном сечении
имеет форму квадрата со сторонойa.
Доказать, что индуктивность такой
катушки определяется выражением .
.
624.
Внутри очень длинного проводящего
стержня радиуса а имеется цилиндрическая
полость радиуса b, ось
которой параллельна оси стержня, он
находится от нее на расстоянииd.
По проводнику течет ток, плотность
которого по сечению однородна и равна
+j. Чему равна напряженность
магнитного поля на оси плоскости, вдали
от концов стержня? (Ответ:![]() ,
где– величина
тока).
,
где– величина
тока).
625. Длина lчугунного тороида по средней линии равна 1,2 м, сечениеS= 20 см2. По обмотке тороида течет ток, создающий в узком вакуумном зазоре магнитный поток Ф = 0,5 мВб. Длинаl0зазора равна 8 мм. Какова должна быть длина зазора, чтобы магнитный поток в нем при той же силе тока увеличился бы в два раза? (Ответ:l1= 1,8 мм).
626.
Тороид с железным сердечником обладает
магнитным сопротивлением Rm= 39![]() 10-3Ом-1с-1. Длина тороида
по средней линииl= 40 см. Определить напряженность магнитного
поля и число ампер-витков, если магнитная
проницаемость в этих условиях μ = 1000,
магнитная индукция
В = 1,25 Тл. (Ответ:
Н = 360 А/м;IN= 360 А витков).
10-3Ом-1с-1. Длина тороида
по средней линииl= 40 см. Определить напряженность магнитного
поля и число ампер-витков, если магнитная
проницаемость в этих условиях μ = 1000,
магнитная индукция
В = 1,25 Тл. (Ответ:
Н = 360 А/м;IN= 360 А витков).
627. Существуют два
проводника, центры которых отстоят на
расстоянии l= 10 см друг от друга. Один из них представляет
собой сплошной бесконечно длинный
цилиндр радиусомr= 2 см,
другой – бесконечно длинный и тонкий
проводник. По этим проводникам текут
токи1= 10 А и2= 5 А в
противоположных направлениях. Определить
напряженность магнитного поля в двух
точкахr1= 1 см иr2= 3 см от центр сплошного проводника.
Дать график зависимости Н = Н(r),
взявr= 0,5![]() nсм, гдеn= 1,2,3,…,8. (Ответ: Н(r1)
= 49,2 А/м; Н(r2) = 69 А/м).
nсм, гдеn= 1,2,3,…,8. (Ответ: Н(r1)
= 49,2 А/м; Н(r2) = 69 А/м).
628. В условиях предыдущей
задачи вычислить Н(r1)
и Н(r2), но в случае
если токи текут в одном направлении.
Дать также график Н(r),
еслиr= 0,5![]() nсм, гдеn= 1,2,3,…,8. (Ответ: Н(r1)
= 31 А/м; Н(r2) = 49 А/м).
nсм, гдеn= 1,2,3,…,8. (Ответ: Н(r1)
= 31 А/м; Н(r2) = 49 А/м).
629. Определить магнитодвижущую силу Fm, необходимую для создания магнитного поля с индукцией В = 1,35 Тл в электромагните со стальным сердечником длинной ℓ = 5 мм. Рассеянием магнитного потока в воздушном промежутке пренебречь. Площадь поперечного сечения тороидаS= 5 см2. (Ответ:Fm= 2,96 кА).
630. Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние ℓ. По проводу течет ток плотности j. Найти вектор индукции магнитного поля внутри полости. Рассмотреть случай, когда= 0. (Ответ: В = ½ μ0[j]).
