Глава 4. Электрическая емкость. Конденсаторы Основные формулы

Электрическая емкость уединенного проводника или конденсатора:

,

где Q– заряд, сообщенный проводнику (конденсатору); – изменение потенциала, вызванное этим зарядом.

Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью,

.

Если сфера полая и заполнена диэлектриком, то электроемкость ее от этого не изменяется.

Электрическая емкость плоского конденсатора:

где S– площадь пластин (каждой пластины);d– расстояние между ними;– диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного nслоями диэлектриком толщинойd_i каждый с диэлектрическими проницаемостями_i (слоистый конденсатор),

Электрическая емкость сферического конденсатора (две концентрические сферы радиусами R₁иR₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью)

Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной lи радиусамиR₁ иR₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью):

Электрическая емкость Cпоследовательно соединенных конденсаторов:

– в общем случае:

где n– число конденсаторов;

– в случае двух конденсаторов:

– в случае n одинаковых конденсаторов электроемкостью C₁ каждый

Электрическая емкость параллельно соединенных конденсаторов:

– в общем случае: .

 – поверхностная плотность заряда, Кл/м².

Энергия электрического поля конденсатора:

Объемная плотность энергии электрического поля в линейной изотропной среде с относительной диэлектрической проницаемостью  следующая:

.

Примеры решения задач

Пример 1. Определить электрическую емкость плоского конденсатора с двумя слоями диэлектриков: фарфора толщинойd₁= 2 мм и эбонита толщинойd₂= 1, 5 мм, если площадьSпластин равна 100 см².

Решение. Емкость конденсатора по определениюгдеQ– заряд на пластинах конденсатора;U– разность потенциалов пластин. Заменив в этом равенстве общую разность потенциаловUсуммойU₁+U₂напряжений на слоях диэлектриков, получим:

(4.1)

Приняв во внимание, что Q=S, равенство (4.1) можно переписать в виде:

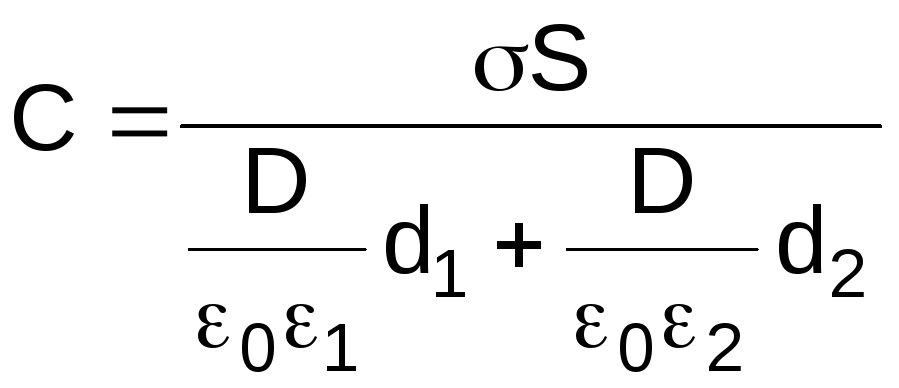(4.2)

где – поверхностная плотность заряда на пластинах;E₁иE₂напряженности поля в первом и втором слоях диэлектрика соответственно;D– диэлектрическое смещение поля в диэлектриках. Умножив числитель и знаменатель равенства (4.2) на₀и учтя, чтоD=, окончательно получим:

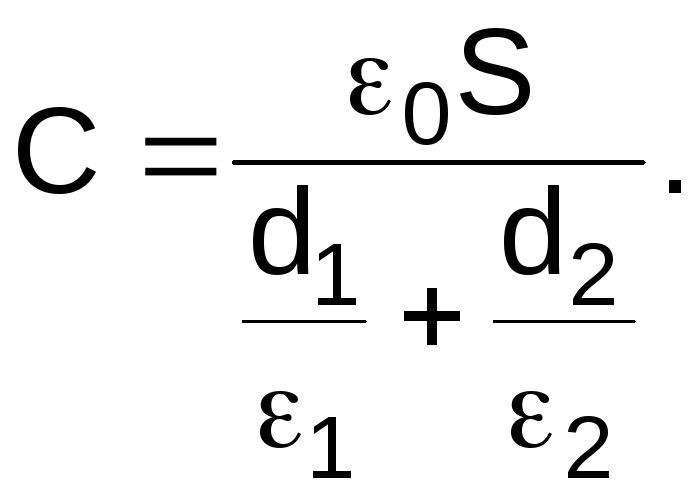(4.3)

Сделав вычисления по формуле (4.3), найдем:

.

Пример 2.Два одинаковых плоских конденсатора соединены параллельно и заряжены до напряженияU₀ = 480 В. После отключения от источника тока расстояние между пластинами одного из конденсаторов уменьшили в два раза. Каким станет напряжениеUна конденсаторах.

Решение. При параллельном соединении конденсаторов их общая емкость будет:

С_бат= С₁+ С₂ =2С ; (С₁= С₂= С).

Заряд батареи q₁= С_батU₀= 2CU₀.

При уменьшении в два раза расстояния между пластинами конденсатора его электроемкость увеличится в два раза (согласно формуле ) и станетC’ = 2C, тогда их общая емкостьC’_бат = 2C+C= 3C.

Заряд станет q₂=C’_батU= 3CU.

По закону сохранения электрического заряда q₁=q₂, так как батарея конденсаторов отключена от источника. Следовательно, 2CU₀= 3CU, откудаВ.

Задачи

401. Найти электроемкость С уединенного металлического шара радиусом R= 1 см. (Ответ: 1,11 пФ).

402. Определите заряды на каждом из конденсаторов вцепи, изображенной на рис. 4.1, если С₁ = 2 мкФ, С₂ = 4 мкФ, С₃= 6 мкФ,= 18 В. (Ответ:Q₁= 30 мкКл;Q₂= 12 мкКл;Q₁= 18 мкКл).

403. Определить электроемкость С земли, принимая ее за шар радиусом R = 6400 км. (Ответ: 180 пФ).

404. Шар радиусом R₁= 6 см заряжен до потенциала φ₁= 300 В, а шар радиусом R₂= 4 см – до потенциала φ₂= 500 В. Определить потенциал φ шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь. (Ответ:).

405. Определите электроемкость С плоского слюдяного конденсатора, площадь S пластин которого равна 100 см², а расстояние между ними равно 0,1 мм (диэлектрическая проницаемость слюды  = 7). (Ответ: 6,2 нФ).

406. Пять конденсаторов одинаковой емкости соединены последовательно в батарею. Параллельно одному из конденсаторов подключен статический вольтметр, емкость которого в два раза меньше емкости каждого конденсатора. Вольтметр показывает 500 В. Какова разность потенциалов на всей батарее? (Ответ: 3500 В).

407. Расстояние d между пластинами плоского конденсатора равно 1,33 мм, площадь S пластин равна 20 см². В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной d₁= 0,7 мм и эбонита толщиной d₂= 0,3 мм. Определите электроемкостьконденсатора (диэлектрическая проницаемость слюды  = 7, эбонита  = 3).(Ответ:

408. N шаровых капель радиусом r заряжены до одинакового потенциала φ₀. Все капли сливаются в одну большую. Определите потенциал и плотность заряда на поверхности большой капли. (Ответ: ).

409. Две концентрические металлические сферы радиусами R₁ = 2 см и R₂ = 2,1 см образуют сферический конденсатор. Определить его электроемкость С, если пространство между сферами заполнено парафином (диэлектрическая проницаемость парафина  = 2). (Ответ:).

410. В плоский конденсатор вдвинули плитку парафина толщиной d = 1 см, которая плотно прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость? (Диэлектрическая проницаемость парафина = 2). (Ответ: 0,5 см).

411. Конденсатор состоит из двух концентрических сфер. Радиус R₁внутренней сферы равен 10 см, внешней R₂= 10,2 см. Промежуток междусферами заполнен парафином. Внутренней сфере сообщен заряд Q = 5 мкКл.Определите разность потенциалов U между сферами. (Диэлектрическая проницаемость парафина= 2). (Ответ: 4, 41 кВ).

412. К воздушному конденсатору, заряженному до разности потенциалов U = 600 В и отключенному от источника напряжения, присоединили параллельно второй незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определите диэлектрическую проницаемость ε фарфора, если после присоединения второго конденсатора разность потенциалов уменьшилась до U₁= 100 В. (Ответ: 5).

413. Два конденсатора электроемкостями С₁= 3 мкФ и С₂= 6 мкФ соединены между собой и присоединены к батарее с эдс, равной 120 В. Определить зарядыQ₁иQ₂конденсаторов и разности потенциаловU₁ иU₂между их обкладками, если конденсаторы соединены: 1) параллельно; 2) последовательно. (Ответ: 360 мкКл; 720 мкКл; 120 В).

414.Конденсатор электроемкостью С1 = 0,2 мкФ был заряжен до разности потенциалов U₁ = 320 В.После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂= 450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С₂второго конденсатора. (Ответ:).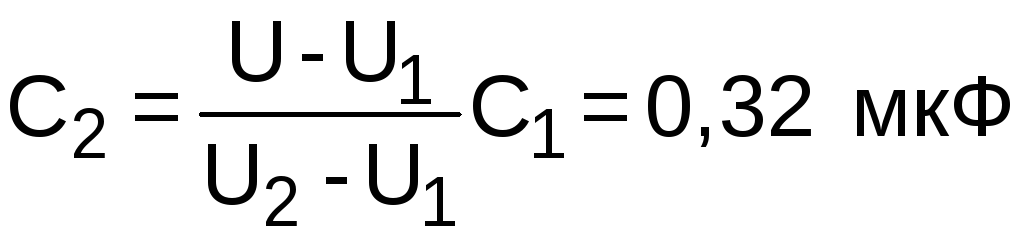

415. Конденсатор электроемкостью С₁= 0,6 мкФ был заряжен до разности потенциаловU₁= 300 В и соединен со вторым конденсаторомэлектроемкостью С₂ = 0,4 мкФ, заряженным до разности потенциалов U₂ = 150 В. Найти заряд ΔQ, перетекший с пластин первого конденсатора на второй. (Ответ:).

416. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 80 пФ. Площадь Sкаждой пластины равна 100 см². Диэлектрик – стекло (= 7). Какова толщинаdстекла? (Ответ: 2, 32 мм).

417. Конденсаторы соединены так, как это показано на рис. 4.2.Электроемкости конденсаторов: С₁ = 0,2 мкФ, С₂ = 0,1 мкФ, С₃ = 0,3 мкФ, С₄ = 0,4 мкФ.Определите электроемкость С батареи конденсаторов. (Ответ: 0, 21 мкФ).

418. Конденсаторы электроемкостями С₁= 10 нФ, С₂= 40 нФ, С₃= 2 нФ, С₄= 30 нФ соединены так, как это показано на рис. 4.3. Определите электроемкость С батареи конденсаторов. (Ответ: 20 пФ).

419. Конденсаторы соединены так, как это показано на рис. 4.4. Электроемкости конденсаторов: С₁= 2 мкФ, С₂= 2 мкФ, С₃= 3 мкФ, С₄= 1 мкФ. Разность потенциалов на обкладках четвертого конденсатораU₄= 100 В. Найти заряды и разности потенциалов на обкладках каждого конденсатора, а также общий заряд и разность потенциалов батареи конденсаторов. (Ответ: 200 мкКл; 120 мкКл;120 мкКл; 100 мкКл; 110 В; 60 В; 40 В; 220 мкКл; 210 В).

420. Конденсаторы электроемкостями С₁= 1 пФ, С₂= 2 пФ, С₃= 2 пФ, С₄= 4 пФ, С₅= 3 пФ соединены так, как это показано на рис. 4.5. Определите электроемкость С батареи конденсаторов. (Ответ: 2 пФ.Указание.Доказать, что если С₁/С₂=С₃/С₄, то φ_A= φ_B, и, следовательно, емкость С₅при определении общей емкости схемы значения не имеет).

421. Плоский конденсатор, между обкладками которого находится пластинка из диэлектрика проницаемости , присоединен к аккумулятору. Заряд конденсатора равенQ₀. Какой заряд ΔQпройдет через аккумулятор при удалении пластинки? (Ответ:).

422. Плоский воздушный конденсатор заряжен до разности потенциалов U= 1000 В. С какой силойFпритягиваются одна к другой его пластины? Площадь пластинS= 100 см², расстояние между нимиd= 1 мм. (Ответ:).

423. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью σ = 0,2 мкКл / м². Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм? (Ответ: 22,6 В).

424. Расстояние dмежду пластинами плоского конденсатора равно 2 см, разность потенциаловU= 6 кВ. ЗарядQкаждой пластины равен 10 нКл. Вычислите энергиюWполя конденсатора и силуFвзаимного притяжения пластин. (Ответ: 30 мкДж).

425. Определите заряды конденсаторовQ₁,Q₂,Q₃в цепи, параметры которой указаны на рис. 4.6.

426. Какое количество теплоты Qвыделится при разряде плоского конденсатора, если разность потенциалов U между пластинами равна 15 кВ, расстояниеd= 1 мм, диэлектрик – слюда и площадьSкаждой пластины равна 300 см². (Ответ:

).

427. Сила Fпритяжения между пластинами плоского воздушного конденсатора равна 50 мН. ПлощадьSкаждой пластины равна 200 см². Найдите плотность энергииwполя конденсатора. (Ответ: 0,209 Дж).

428. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние d₁ между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U = 1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d₂ = 3,5 см. (Ответ: 2,5 Дж/м³).

429. Конденсаторы электроемкостями С₁= 1 мкФ, С₂= 2 мкФ С₃= 3 мкФ включены в цепь с напряжениемU= 1,1 кВ. Определите энергию каждого конденсатора в случаях: 1) последовательного их включения; 2) параллельного включения. (Ответ: 50 мкДж).

430. Электроемкость С плоского конденсатора равна 111 пФ. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U= 600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало. (Ответ: 0,18 Дж).