
- •Электричество и магнетизм Сборник задач по курсу общей физики
- •Предисловие
- •Глава 1. Закон Кулона. Закон сохранения электрического заряда. Напряженность электрического поля Основные формулы
- •Примеры решения задач
- •Глава 2. Электрический диполь Основные формулы
- •Примеры решения задач
- •Глава 3. Вычисление полей с помощью теоремы Гаусса Основные формулы
- •Примеры решения задач
- •Глава 4. Электрическая емкость. Конденсаторы Основные формулы
- •Примеры решения задач
- •Глава 5. Энергия системы точечных зарядов Основные формулы
- •Примеры решения задач
- •Глава 6. Закон полного тока. Магнитный поток. Магнитные цепи. Сверхсильные магнитные поля Основные формулы и соотношения
- •Примеры решения задач
- •Глава 7. Действие магнитного поля на ток и заряд Основные формулы и соотношения
- •Примеры решения задач
- •Глава 8. Магнитный поток. Работа по перемещению проводника с током в магнитном поле Основные формулы и соотношения
- •Глава 9. Закон электромагнитной индукции. Индуктивность. Энергия магнитного поля
- •Основные формулы и соотношения
- •Примеры решения задач
- •Глава 10. Магнитное поле в веществе. Магнитные жидкости Основные формулы и соотношения
- •Примеры решения задач
- •Глава 11. Уравнения максвелла Основные формулы и соотношения
- •Примеры решения задач
- •Заключение
Глава 11. Уравнения максвелла Основные формулы и соотношения
1. Уравнения Максвелла в дифференциальной форме:
![]() ;
;
![]() ;
(11.1)
;
(11.1)
![]() ;
;
![]() ,
(11.2)
,
(11.2)
где
![]() – ток смещения.
– ток смещения.
Формулы преобразования полей при переходе от К-системы отсчета к движущейся по отношению к ней со скоростью
 К’-системе:
К’-системе:
 ;
;
 ;
(11.3)
;
(11.3)
 ,
,
 ,
(11.4)
,
(11.4)
где
символы
![]() и
и![]() обозначают составляющие полей,
параллельные и перпендикулярные к
вектору
обозначают составляющие полей,
параллельные и перпендикулярные к
вектору![]() .
.
3. Плотность потока электромагнитной энергии (вектор Пойнтинга S) и объемная плотность энергии электромагнитного поля W:
![]() .
(11.5)
.
(11.5)
![]() .
(11.6)
.
(11.6)
4.
Для медленно меняющихся полей (![]() )
справедливо квазистационарное
приближение:
)
справедливо квазистационарное
приближение:
![]() ;
;
![]() ;
(11.7)
;
(11.7)
![]() ;
;
![]() ;
(11.8)
;
(11.8)
Используя данные уравнения, получаем выражения для полей:
![]() ;
(11.9)
;
(11.9)
![]() .
(11.10)
.
(11.10)
Примеры решения задач
Пример
1.
Сравнить величину токов проводимости
и смещения в среде с проводимостью
![]() и относительной диэлектрической
проницаемостью
и относительной диэлектрической
проницаемостью![]() для частоты поля
для частоты поля![]() .
.
Решение.
Ток смещения в среде обусловлен переменным
электрическим полем
![]() .
Отсюда мгновенное значение плотности
тока проводимости j, обусловленное
этим полем, находится по закону Ома:
.
Отсюда мгновенное значение плотности
тока проводимости j, обусловленное
этим полем, находится по закону Ома:
![]() .
(11.11)
.
(11.11)
Плотность тока смещения находится как
![]() .
(11.12)
.
(11.12)
Из формул (11.11) и (11.12) получаем:
![]() .
(11.13)
.
(11.13)
Отношение амплитудных значений:
![]() .
(11.14)
.
(11.14)
Пример 2. Найти электрическое поле, создаваемое точечным зарядом q, движущимся с постоянной скоростью v.
Решение.
В собственной системе отсчета
![]() заряда имеется лишь электрическое поле
с напряженностью
заряда имеется лишь электрическое поле
с напряженностью
![]() .
(11.15)
.
(11.15)
Применяем формулы преобразования полей (11.3) и (11.4), получающиеся обращением данных, т. е. выражаем поле в неподвижной системе координат К через поля в движущейся системе К’:
![]() ; (11.16)
; (11.16)
![]() .(11.17)
.(11.17)
где
![]() .
Из формул (11. 16) и (11.17) имеем:
.
Из формул (11. 16) и (11.17) имеем:
![]() .
(11.18)
.
(11.18)
Подставляя в это выражение формулу (11.15), и учитывая, что
![]() (11.19)
(11.19)
получаем ответ:
 .
(11.20)
.
(11.20)
Пример
3.
Найти глубину проникновения
квазистационарного поля в проводник,
занимающий пространство z
> 0. Проводимость материала проводника
![]() ,
магнитная проницаемость
,
магнитная проницаемость![]() .
.
Решение. Выберем поверхность проводника в качестве плоскости z=0. Ввиду однородности задачи по направлениям x и y искомое поле зависит только от координаты z. В квазистационарном приближении уравнения для Е и Н выглядят следующим образом:
![]() ,
,
![]() ,
,
где
![]() .
.
Решение уравнения имеет вид:
![]() ,
,
где
![]() – глубина проникновения поля в проводник.
– глубина проникновения поля в проводник.
Задачи
1101.
Две частицы, масса каждой из которых
равна m,
а заряды q и -q движутся под действием
электрического притяжения по окружности
вокруг общего центра масс так, что
соединяющая их прямая вращается с
угловой скоростью
![]() .
Найти плотность тока смещения в центре
этой системы.
(Ответ:
.
Найти плотность тока смещения в центре
этой системы.
(Ответ:![]() )
.
)
.
1102.
Точечный заряд движется с нерелятивистской
скоростью v = const.
Воспользовавшись теоремой о циркуляции
вектора Н по окружности, плоскость
которой перпендикулярна траектории,
найти магнитное поле H
в точке А на этой окружности как функцию
радиус-вектора r
и скорости V
заряда. (Ответ:
![]() ).
).
1103. Доказать с помощью уравнений Максвелла, что переменное во времени магнитное поле не может существовать без электрического поля (неоднородного в пространстве).
1104.
Вывести из уравнений Максвелла закон
сохранения электрического заряда:
![]() ,
где
,
где![]() – плотность заряда; j – плотность тока.
– плотность заряда; j – плотность тока.
1105.
Пространство между обкладками плоского
конденсатора, имеющими форму круглых
дисков, заполнено однородной, слабо
проводящей средой с удельной
проводимостью
![]() и диэлектрической проницаемостью
и диэлектрической проницаемостью![]() .
Найти напряженность магнитного поля
между обкладками на расстоянииr
от
их оси, если на конденсатор подано
переменное напряжение
.
Найти напряженность магнитного поля
между обкладками на расстоянииr
от
их оси, если на конденсатор подано
переменное напряжение
![]() .
Расстояние между обкладками d, краевыми
эффектами пренебречь. (Ответ:
.
Расстояние между обкладками d, краевыми
эффектами пренебречь. (Ответ:![]() ).
).
1106.
Длинный прямой соленоид имеет
n
витков на единицу длины. По нему течет
переменный ток
![]() .
Найти плотность тока смещения как
функцию расстоянияr
от
оси соленоида, радиус сечения которого
R. (Ответ:
.
Найти плотность тока смещения как
функцию расстоянияr
от
оси соленоида, радиус сечения которого
R. (Ответ:![]()

![]() ;
;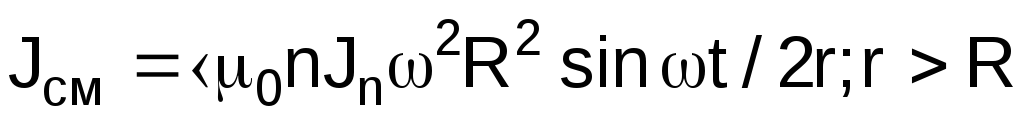 ).
).
1107.
Точечный заряд движется с нерелятивистской
скоростью
v = const. Найти плотность тока
смещения
![]() в точке, находящейся на расстоянииr
от
заряда на прямой, перпендикулярной к
траектории и проходящей через заряд.
(Ответ:
в точке, находящейся на расстоянииr
от
заряда на прямой, перпендикулярной к
траектории и проходящей через заряд.
(Ответ:
![]() .
.
1108.
Определить электрический дипольный
момент плоского линейного кругового
тока J радиуса а,
перемещающегося со скоростью V, магнитный
момент кольца равен
![]() .
(Ответ:
.
(Ответ:![]() ).
).
1109. Показать, что вращательное движение среды не приводит к генерации магнитного поля.
1110.
Найти характерное время рассасывания
свободных зарядов под действием
кулоновского отталкивания в однородной
и изотропной среде с диэлектрической
проницаемостью
![]() и проводимостью
и проводимостью
![]() .
(Ответ:
.
(Ответ:
![]() ).
).
1111. Доказать, что отсутствие сопротивления у сверхпроводников является следствием эффекта Мейсснера (внутри сверхпроводника магнитное поле В = 0).
1112.
В инерциальной
![]() -системе
отсчета имеется два однородных
взаимно-перпендикулярных поля:
электрическое (напряженностью Е = 40
кВ/м)и
магнитное (индукцией В = 0,20 мТл). Найти
индукцию В поля в системе
-системе
отсчета имеется два однородных
взаимно-перпендикулярных поля:
электрическое (напряженностью Е = 40
кВ/м)и
магнитное (индукцией В = 0,20 мТл). Найти
индукцию В поля в системе
![]() ,
где наблюдается только одно магнитное
поле. Указание – воспользоваться
инвариантами поля. (Ответ: В = 0,15 мТл).
,
где наблюдается только одно магнитное
поле. Указание – воспользоваться
инвариантами поля. (Ответ: В = 0,15 мТл).
1113.
Пластина из неферромагнитного металла
движется со скоростью V = 90 см/с в однородном
магнитном поле В = 50 мТл. Вектора V и В
лежат в плоскости пластины и перпендикулярны
друг другу. Найти поверхностную
плотность электрических зарядов,
возникающих на пластине вследствие ее
движения. (Ответ:
![]() ).
).
1114.
Длинный цилиндр радиуса а
из диэлектрика с проницаемостью
![]() вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью![]() вокруг своей оси во внешнем однородном
магнитном поле В, причем
вокруг своей оси во внешнем однородном
магнитном поле В, причем![]() .
Найти поляризованность диэлектрика
как функцию расстояния от оси цилиндра.
(Ответ:
.
Найти поляризованность диэлектрика
как функцию расстояния от оси цилиндра.
(Ответ:![]() ).
).
1115. Нерелятивистский
точечный заряд q движется с постоянной
скоростью V.
Найти с помощью формул преобразования
полей индукцию В магнитного поля этого
заряда в точке, положение которой
относительно заряда определяется
радиусом-вектором r.
(Ответ:
![]() ).
).
1116.
Доказать инвариантность (т. е.
независимость от системы отсчета)
следующих величин: (![]() )
и
)
и![]() .
.
1117. Показать с помощью формул преобразования полей, что если в инерциальной k-системе отсчета имеется только электрическое или только магнитное поле, то в любой другой инерциальной k'-системе будут существовать как электрическое, так и магнитное поля одновременно, причем Е' = ∫ В'.
1118.
По прямому проводнику круглого сечения
течет постоянный ток .
Найти поток вектора Пойнтинга
![]() через боковую поверхность участка
данного проводника, имеющего сопротивление
R.
(Ответ:
через боковую поверхность участка
данного проводника, имеющего сопротивление
R.
(Ответ:
![]() ).
).
1119.
Шар радиуса R = 50 см находится в немагнитной
среде с диэлектрической
проницаемостью
![]() .
В среде распространяется плоская
электромагнитная волна, длина которой
.
В среде распространяется плоская
электромагнитная волна, длина которой![]() и амплитуда электрической составляющей
Е0
=
200 В/м. Какая энергия падает на шар за
время t = 1 мин?
(Ответ: W = 5 кДж).
и амплитуда электрической составляющей
Е0
=
200 В/м. Какая энергия падает на шар за
время t = 1 мин?
(Ответ: W = 5 кДж).
1120.
Найти средний вектор Пойнтинга <S>
у плоской электромагнитной волны
![]() ,
если волна распространяется в вакууме.
(Ответ:
,
если волна распространяется в вакууме.
(Ответ:![]() ).
).
1121.
Плоская электромагнитная волна с
частотой
![]() = 10 МГц распространяется в слабо
проводящей среде с удельной проводимостью
= 10 МГц распространяется в слабо
проводящей среде с удельной проводимостью![]() и диэлектрической проницаемостью
и диэлектрической проницаемостью![]() .
Найти отношение амплитуд плотностей
токов проводимости и смещения. (Ответ:
.
Найти отношение амплитуд плотностей
токов проводимости и смещения. (Ответ:![]() ).
).
1122.
Солнечные лучи при перпендикулярном
падении ежесекундно приносят на
земную поверхность поток энергии
![]() .
Вычислить среднеквадратичные значения
векторов Е и Н в солнечных лучах. (Ответ:
Е = 750 В/м; Н = 2 А/м).
.
Вычислить среднеквадратичные значения
векторов Е и Н в солнечных лучах. (Ответ:
Е = 750 В/м; Н = 2 А/м).
1123.
Полупространство z > о заполнено
проводником с проводимостью
![]() ,
магнитной проницаемостью
,
магнитной проницаемостью![]() .
Параллельно плоскости z = 0 имеется
электрическое поле
.
Параллельно плоскости z = 0 имеется
электрическое поле![]() .
Найти поле в проводнике. (Ответ:
.
Найти поле в проводнике. (Ответ:![]() ).
).
1124.
Металлический шар радиуса а
с проводимостью
![]() и магнитной проницаемостью
и магнитной проницаемостью![]() помещен в однородное переменное поле
помещен в однородное переменное поле![]() .
Считая частоту малой (квазистационарное
приближение), найти среднюю мощность,
поглощаемую шаром. (Ответ:
.
Считая частоту малой (квазистационарное
приближение), найти среднюю мощность,
поглощаемую шаром. (Ответ:![]() ).
).
1125.
Металлический шар помещен в однородное
магнитное поле, меняющееся с частотой
![]() .
Найти среднюю поглощаемую шаром мощность
при больших частотах. Радиус шараа,
магнитная проницаемость
.
Найти среднюю поглощаемую шаром мощность
при больших частотах. Радиус шараа,
магнитная проницаемость
![]() ,
проводимость
,
проводимость![]() .
При определении поля внутри шара считать
его поверхность плоской. (Ответ:
.
При определении поля внутри шара считать
его поверхность плоской. (Ответ:![]() ).
).
1126.
Найти плотность тока смещения в плоском
конденсаторе, пластины которого
раздвигаются со скоростью V0,
оставаясь параллельными друг к другу,
если разность потенциалов
U
между пластинами остается постоянной.
(Ответ:
![]() ).
).
1127. Показать, что при разрядке сферического конденсатора, ток проводимости на его обкладках совпадает с током смещения.
1128.
Найти сопротивление 1 см цилиндрического
провода радиуса
![]() для переменного электрического поля с
частотой
для переменного электрического поля с
частотой![]() .
Проводимость материала провода
.
Проводимость материала провода![]() ,
для описания электрического поля
использовать квазистационарное
приближение. (Ответ:
,
для описания электрического поля
использовать квазистационарное
приближение. (Ответ:![]() ).
).
1129.
Найти эдс Е униполярной машины,
представляющей собой постоянный
сферический магнит радиуса
![]() с магнитным моментом М0,
вращающийся с угловой скоростью
с магнитным моментом М0,
вращающийся с угловой скоростью
![]() .
Один из подвижных контактов расположен
на полюсе, а другой – на экваторе. (Ответ:
.
Один из подвижных контактов расположен
на полюсе, а другой – на экваторе. (Ответ:![]() ).
).
1130.
Определить магнитный момент неравномерно
вращающегося шара радиуса
![]() .
Проводимость материала шара
.
Проводимость материала шара![]() ,
угловая скорость вращения
,
угловая скорость вращения![]() считается малой, так что глубина
проникновения поля
считается малой, так что глубина
проникновения поля![]() .
(Ответ:
.
(Ответ:![]() ).
).
